华东交通大学2018年ACM“双基”程序设计竞赛部分题解
链接:https://ac.nowcoder.com/acm/contest/221/C
来源:牛客网
C-公式题(2)
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 32768K,其他语言65536K
64bit IO Format: %lld
空间限制:C/C++ 32768K,其他语言65536K
64bit IO Format: %lld
题目描述
令f(n)=2*f(n-1)+3*f(n-2)+n,f(1)=1,f(2)=2
令g(n)=g(n-1)+f(n)+n*n,g(1)=2
告诉你n,输出g(n)的结果,结果对1e9+7取模
令g(n)=g(n-1)+f(n)+n*n,g(1)=2
告诉你n,输出g(n)的结果,结果对1e9+7取模
输入描述:
多组输入,每行一个整数n(1<=n<=1e9),如果输入为0,停止程序。
输出描述:
在一行中输出对应g(n)的值,结果对1e9+7取模。
备注:
项数极大,朴素算法无法在规定时间内得出结果
解题思路:很明显的矩阵快速幂,比赛时没推出来。推出来了就是一个矩阵快速幂的板子题。
推倒方法可以参照:https://www.jianshu.com/p/25eba927d9da
推倒过程:
g(n)=g(n-1)+f(n)+n*n;
g(n)=g(n-1)+2*f(n-1)+3*f(n-2)+n*n+n;
g(n)=g(n-1)+2*f(n-1)+3*f(n-2)+(n-1)^2+3*(n-1)+2;
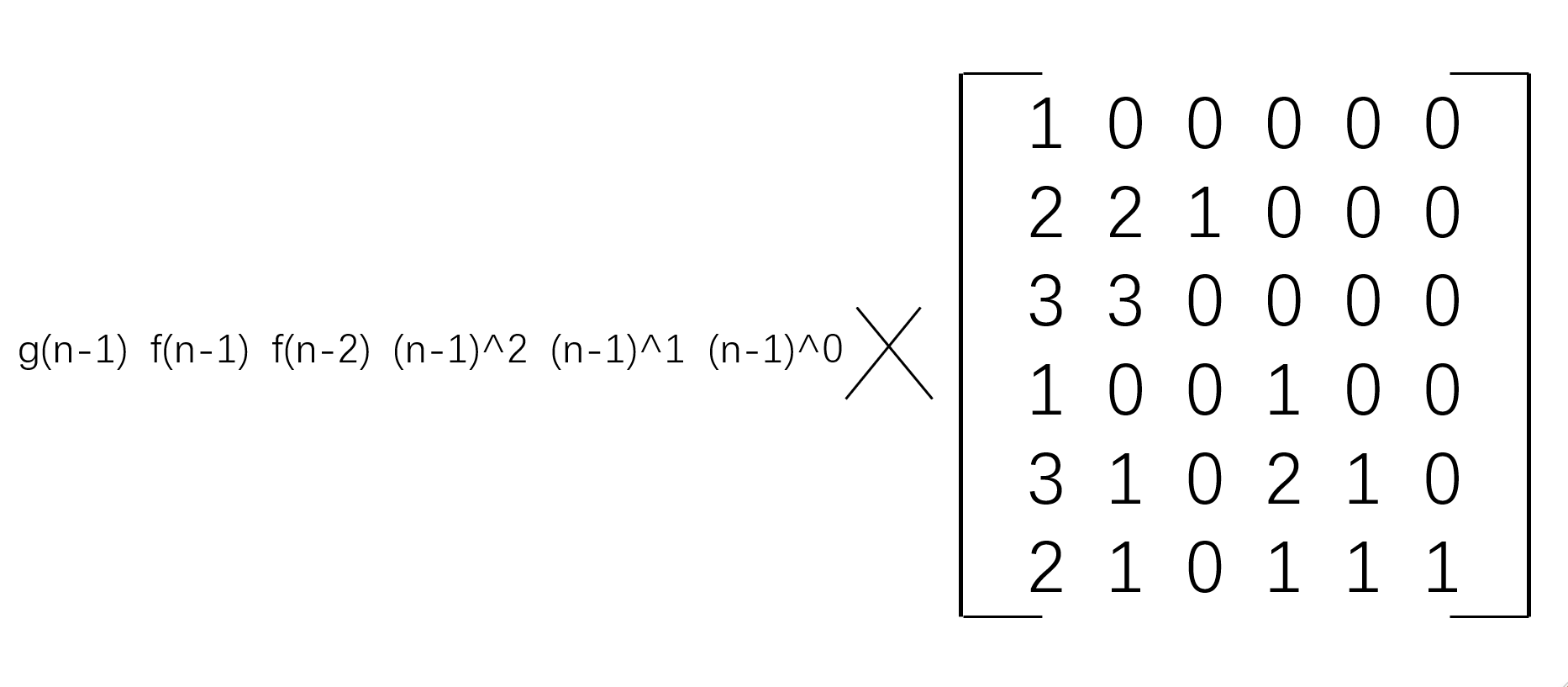
得到矩阵:

再通过简单的递推一下,左边n代3,可以得到一个常数矩阵,再乘以右边矩阵的n-2次方,得到矩阵的第一行第一列元素即为答案。
#include <iostream> #include <cstdio> #include <cstring> #include <cmath> #include <algorithm> #include <queue> using namespace std; const int mod=1e9+7; const int maxn=6; typedef long long ll; ll n; struct Matrix{ ll a[maxn][maxn]; }; Matrix mul(Matrix a,Matrix b) //两矩阵相乘 { Matrix temp; memset(temp.a,0,sizeof(temp.a)); for(int i=0;i<maxn;i++) for(int j=0;j<maxn;j++) for(int k=0;k<maxn;k++) temp.a[i][j]=(temp.a[i][j]+a.a[i][k]*b.a[k][j])%mod; return temp; } Matrix qpow(Matrix a,ll n) //矩阵快速幂 { Matrix ans; memset(ans.a,0,sizeof(ans.a)); for(int i=0;i<maxn;i++) ans.a[i][i]=1; //化成单位矩阵 while(n) { if(n&1) ans=mul(ans,a); a=mul(a,a); n/=2; } return ans; } int main() { Matrix A,C; A.a[0][0]=1,A.a[0][1]=0,A.a[0][2]=0,A.a[0][3]=0,A.a[0][4]=0,A.a[0][5]=0; A.a[1][0]=2,A.a[1][1]=2,A.a[1][2]=1,A.a[1][3]=0,A.a[1][4]=0,A.a[1][5]=0; A.a[2][0]=3,A.a[2][1]=3,A.a[2][2]=0,A.a[2][3]=0,A.a[2][4]=0,A.a[2][5]=0; A.a[3][0]=1,A.a[3][1]=0,A.a[3][2]=0,A.a[3][3]=1,A.a[3][4]=0,A.a[3][5]=0; A.a[4][0]=3,A.a[4][1]=1,A.a[4][2]=0,A.a[4][3]=2,A.a[4][4]=1,A.a[4][5]=0; A.a[5][0]=2,A.a[5][1]=1,A.a[5][2]=0,A.a[5][3]=1,A.a[5][4]=1,A.a[5][5]=1; C.a[0][0]=8,C.a[0][1]=2,C.a[0][2]=1,C.a[0][3]=4,C.a[0][4]=2,C.a[0][5]=1; while(cin>>n) { if(n==0) break; if(n==1) { cout<<2<<endl; continue; } cout<<mul(C,qpow(A,n-2)).a[0][0]<<endl; } return 0; }
链接:https://ac.nowcoder.com/acm/contest/221/G
来源:牛客网
G-7的意志
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 32768K,其他语言65536K
64bit IO Format: %lld
空间限制:C/C++ 32768K,其他语言65536K
64bit IO Format: %lld
题目描述
定义一个序列a:7,77,777......,7777777(数字全为7的正整数,且长度可以无限大)
clearlove7需要从含有7的意志的数里获得力量,如果一个整数能被序列a中的任意一个数字整除,并且其数位之和为序列a中任意一个数字的倍数,那么这个数字就含有7的意志,现在给你一个范围[n,m],问这个范围里有多少个数字含有7的意志。
clearlove7需要从含有7的意志的数里获得力量,如果一个整数能被序列a中的任意一个数字整除,并且其数位之和为序列a中任意一个数字的倍数,那么这个数字就含有7的意志,现在给你一个范围[n,m],问这个范围里有多少个数字含有7的意志。
输入描述:
多组输入,每行两个个整数n,m(1<=n<=m<=1e18),如果输入为"0 0",停止程序。
输出描述:
每一行输出含有7的意志的数的个数。
数位dp,不会可以参考博客:https://blog.csdn.net/brazy/article/details/77427699
定义一个三维dp,分别存储到枚举的当前位置,模7的余数,数位和模7的余数。
#include<cstdio> #include<cstring> #include<algorithm> #include<iostream> #include<string> #include<vector> #include<stack> #include<bitset> #include<cstdlib> #include<cmath> #include<set> #include<list> #include<deque> #include<map> #include<queue> using namespace std; typedef long long ll; const double PI = acos(-1.0); const double eps = 1e-6; const int INF = 0x3f3f3f3f; const ll mod=1e9+7; ll gcd(ll a,ll b){return b?gcd(b,a%b):a;} ll n,m,a[20]; ll dp[20][20][20]; ll dfs(ll pos,ll pre,ll sum,bool limit) { if(pos==-1) return (pre%7==0&&sum%7==0); //枚举到了最后一位并且合法 if(!limit&&dp[pos][pre][sum]!=-1) return dp[pos][pre][sum]; ll up=limit?a[pos]:9; ll ans=0; for(int i=0;i<=up;i++) ans+=dfs(pos-1,(pre*10+i)%7,(sum+i)%7,limit&&i==a[pos]); if(!limit) //记忆化 dp[pos][pre][sum]=ans; return ans; } ll solve(ll x) { ll pos=0; while(x) //对数进行数位拆分 { a[pos++]=x%10; x/=10; } return dfs(pos-1,0,0,true); //从最高位开始枚举 } int main() { ios_base::sync_with_stdio(false); cin.tie(0); memset(dp, -1, sizeof(dp)); while(cin>>n>>m) { if(n==0&&m==0) break; cout<<solve(m)-solve(n-1)<<endl; } return 0; }
链接:https://ac.nowcoder.com/acm/contest/221/I
来源:牛客网
I-数学题
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 32768K,其他语言65536K
64bit IO Format: %lld
空间限制:C/C++ 32768K,其他语言65536K
64bit IO Format: %lld
题目描述
题面描述
最近,华东交通大学ACM训练基地的老阿姨被一个数学问题困扰了很久,她希望你能够帮她解决这个问题。
这个数学问题是这样的,给你一个N,要求你计算
最近,华东交通大学ACM训练基地的老阿姨被一个数学问题困扰了很久,她希望你能够帮她解决这个问题。
这个数学问题是这样的,给你一个N,要求你计算

gcd(a,b)表示a和b的最大公约数
输入描述:
多组输入,每行一个整数n(1<=n<=10^14)。
输出描述:
每行一个整数,表示答案。由于答案会很大你要对1000000007取模。
示例1
说明
样例一,2+4=6。
样例二,2+4+5+6+8+10=35。
思路:欧拉公式的延伸:对于一个数,与其互质的数的总和是euler(n)*n/2。
所以结果就是n*(n+1)/2-euler(n)*n/2.
注意取模不能直接除2,需要乘2对1e9+7的逆元。
#include<bits/stdc++.h> using namespace std; typedef long long ll; const ll mod=1e9+7; ll n,m; ll euler(ll n) { ll ans=n; ll i; for(i=2;i<=sqrt(n);i++) { if(n%i==0) { ans=ans/i*(i-1); while(n%i==0) n/=i; } } if(n>1) ans=ans/n*(n-1); return ans; } ll pow_mod(ll a, ll b) { ll ret = 1; ll p=mod; while(b) { if(b & 1) ret = (ret * a) % p; a = (a * a) % p; b >>= 1; } return ret; } int main() { while(cin>>n) { if(n==1) { cout<<0<<endl; continue; } ll inv=pow_mod(2,mod-2); cout<<((n%mod)*((n+1-euler(n))%mod)%mod)*inv%mod<<endl; } return 0; }
链接:https://ac.nowcoder.com/acm/contest/221/K
来源:牛客网
MIKU酱的氪金宝典
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 32768K,其他语言65536K
64bit IO Format: %lld
空间限制:C/C++ 32768K,其他语言65536K
64bit IO Format: %lld
题目描述
MIKU酱是个玩游戏氪金的人,游戏公司给她制定了新的规则,如果想从关卡i到关卡j,你需要交一些钱就可以了,但同时,MIKU酱的爸爸zjw很爱她,所以她可以每过一关就向她爸要一次钱,但她爸每次给他的钱是固定的,MIKU酱是个不会节省的女孩,哪怕每次多出来的钱,她也会拿去买肥宅快乐水,所以每次要的钱一定花完,因为MIKU酱不想挨骂,所以希望每次他爸给她的钱最少。
tips(到达第n关即通过,每到达一关一定能通过这关)
输入描述:
多组输入,每个样例第一行输入两个整数n,m(2<=n<=200,1<=m<=1000)表示关卡和规则的数量,接下来m行规则,每行输入x,y,w(w<=1000),表示从关卡x到y需要缴纳w的费用,保证题目有解,不会出现x=y的情况
输出描述:
输出一行,代表最少的钱
思路:n的范围不大,三层循环就可以过,但是比赛时没想到,比赛用的dfs,但是超时,经过剪枝了下,还是过了,题解用的dijkstra
dfs是记录两个东西,一个当前位置,一个该条路的边权最大值,走到节点n时,ans保留dfs出的最小值。
dijkstra做法直接把松弛操作改改就可以了
dfs做法:
#include<bits/stdc++.h> using namespace std; typedef long long ll; const ll mod=1e9+7; const ll inf=0x3f3f3f3f; ll n,m; typedef pair<int,int> P; vector<P> mp[1005]; int vis[1005],ans; void dfs(int x,int cost) //x为当前位置,cost为该条路的边权最大值 { if(x==n) { ans=min(ans,cost); return; } if(cost>=ans) //剪枝,如果还未到n就已经比现在最优结果大直接返回,去掉会超时 return; int ss=mp[x].size(); for(int i=0;i<ss;i++) { if(vis[mp[x][i].first]==0) { vis[mp[x][i].first]=1; dfs(mp[x][i].first,max(cost,mp[x][i].second)); vis[mp[x][i].first]=0; } } } int main() { while(cin>>n>>m) { ios_base::sync_with_stdio(false); cin.tie(0); for(int i=1;i<=n;i++) mp[i].clear(); ans=inf; memset(vis,0,sizeof(vis)); for(int i=1;i<=m;i++) { int u,v,w; cin>>u>>v>>w; P q; q.first=v; q.second=w; mp[u].push_back(q); } vis[1]=1; dfs(1,0); cout<<ans<<endl; } return 0; }
dijkstra做法:
#include<cstdio> #include<cstring> #include<algorithm> #include<iostream> #include<string> #include<vector> #include<stack> #include<bitset> #include<cstdlib> #include<cmath> #include<set> #include<list> #include<deque> #include<map> #include<queue> using namespace std; typedef long long ll; const double PI = acos(-1.0); const double eps = 1e-6; const int INF = 0x3f3f3f3f; const ll mod=1e9+7; int n,m,dis[100005],vis[205]; struct qnode{ int v,d; qnode(int a,int b):v(a),d(b){} bool operator<(const qnode& a)const{ return d>a.d; } }; struct edge{ int v,w; edge(int a,int b):v(a),w(b){} }; vector<edge> mp[1005]; priority_queue<qnode> pq; void dij() { memset(vis,0,sizeof(vis)); memset(dis,INF,sizeof(dis)); dis[1]=0; pq.push(qnode(1,0)); while(!pq.empty()) { qnode x=pq.top(); pq.pop(); int u=x.v; for(int i=0;i<mp[u].size();i++) { int v=mp[u][i].v; int w=mp[u][i].w; int tmp=dis[u]; tmp=max(dis[u],w); if(dis[v]>tmp) //如果该条路边权最大值小于当前最优值,则更新 { dis[v]=tmp; pq.push(qnode(v,dis[v])); } } } } int main() { ios_base::sync_with_stdio(false); cin.tie(0); while(cin>>n>>m) { for(int i=1;i<=n;i++) mp[i].clear(); for(int i=0;i<m;i++) { int u,v,w; cin>>u>>v>>w; mp[u].push_back(edge(v,w)); } dij(); cout<<dis[n]<<endl; } return 0; }



