向量

前言

将本部分从线性代数学习笔记中分离了出来，因为一方面学习笔记不应当篇幅太长，另一方面这也是平面几何的前置知识。

向量

所谓向量，字面意思，就是一个 \(n\) 元组。

将其写成：

\[\begin{bmatrix} a_1 \\ a_2 \end{bmatrix} \]

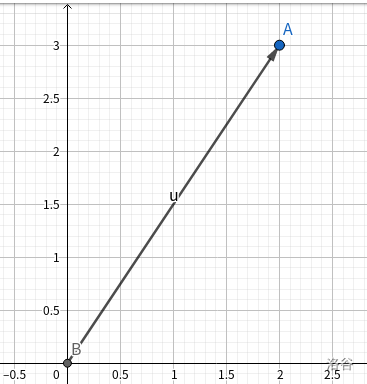
\( \begin{bmatrix} 2 \\ 3 \end{bmatrix} \) 的图像为：

---

点积和叉积

我们知道有点积和叉积。

两个向量的点积：\(a\cdot b=a^T\times b\)

就是矩阵乘法，最后的结果是个数值。

注：\(a_T\) 表示向量 \(a\) 的转置。因为矩阵乘法的限制所以这里需要将其转置一下才能进行此运算。

至于实际意义的话，一般用于计算向量之间的夹角，应用比较广泛。

两个向量的叉积：

以二维为例，其中 \(i,j,k\) 表示三个方向上的单位向量（二维方向两个正方向和垂直二维平面的正方向）。

\[a\wedge b= det \begin{vmatrix} i & j & k\\ x_a & y_a & z_a\\ x_b & y_b & z_b \end{vmatrix} \]

行列式的计算公式后面讲。

实际意义：二维意义下表示向量所形成的平行四边形的有向面积，三维意义下的混合积 \([abc]=(a\wedge b)\wedge c\)，可以得到以 \(a,b,c\) 为棱的平行六面体的体积。