解题报告
解题报告
https://www.luogu.com.cn/blog/zjjws-luogu-com/xie-ti-bao-gao
https://www.cnblogs.com/zjjws/p/13769602.html
Part 1:题解
T1
首先,考虑当前取的三个数 \(x,y,z\),满足 \(x\le y\le z\)。
那么如果要判断是否能构成三角形只需要考虑 \(x+y>z\) 是否满足,因为另外两个不等式明显成立。
那么对于一个固定的 \(z\),能找到的最可能满足条件的 \(x,y\),就是按升序排序后在 \(z\) 前面的两个数。即对于序列 \(a\):
如果没有三角形的话,就得满足:
考虑这样的序列。在一定的值域内,如果要使序列长度 \(p\) 尽量大,那么那些不等式自然是取等号最优,且 \(a_1\) 和 \(a_2\) 要尽量小。那一定值域内 \(p\) 最大的不能选出三角形三边的序列就是个斐波那契数列。
写个程序跑一下发现第 \(40\) 项就已经大于题目给定的值域 \(10^8\) 了。
那么对于一个询问的区间,如果区间长度大于 \(40\),那肯定有解,否则 sort 一下暴力跑。
T2
考虑对于一个时间段,我们的选择策略:
很明显的贪心,当选择 \(x\) 个数时,定然是从大到小选 \(x\) 个数最优。
那么暴力的做法就是从大到小扫过去,设这个数为 \(a\),是第 \(b\) 大的数,则它的贡献为:
子任务1-4
暴力应该可以艹过去,关于这点 Rui_R 已经证明过了。
子任务5
对于每个处于直播开始或结束的时间段暴力算出答案,复杂度 \(\operatorname O(2n\sqrt n)\)。
子任务6
我们会发现对于每一个数,它有两个量,分别是自己和它当前的 Rank 值(即从大到小的排名),而且只有 Rank 值是会变化的。
https://www.luogu.com.cn/problem/U132399
Point_King 的这道题目的 \(50\) 分部分分就是这个问题:二元组,其中一元恒定,贡献为乘积,求最大贡献。
考虑值域分块,块内维护一个凸包,每次有不完整修改的就直接暴力重构。
每次求答案的时候从后往前扫,如果加上这个块内的数以后总个数超过 \(\frac{m}{2}\) 就在这个块停下,暴力做这一个块。(边界细节自己去写,这里说得比较粗略)
那么对于没有触碰到边界的块,块内最大值是可以二分求得的,如果学过斜率优化应该都知道怎么去实现。
T3
子任务1-2
可以直接 \(n^2\) 暴力枚举区间,其中子任务 \(2\) 还需要打个 st 表。
子任务3
随机数据 \(\dots\) 我是没有想到什么靠谱的做法,也许可以由 _Wallace_ 来讲讲。
子任务4
升序序列,一个区间的贡献为左端点异或右端点的值,建一颗 Trie 树就好了。
子任务5
对于一个合法的区间:
会发现 \(\max\) 右边和 \(\min\) 左边的数都是无用的,不一定能加,并且加了也毫无贡献,真正重要的就是中间的那一段。
那么一个合法区间只需满足:以左端点为 \(\min\),右端点为 \(\max\),中间所有数 \(x\in(\min,\max)\)。
(因为是排列,所以可以写开区间)
于是这样你就得到了形式化题面:
给定长度为 \(n\) 的排列 \(\{a_1, a_2, \cdots, a_n\}\),定义一个区间 \([l, r](l<r)\) 是“近似升序”的,那么当且仅当 \(\forall k\in (l, r)\),满足 \(a_l <a_k < a_r\)。对于长度为 \(2\) 的区间,如果满足 \(a_l < a_r\) 那么也符合要求。
对于所有的近似有序区间 \([l_1, r_1], [l_2, r_2], \cdots, [l_d, r_d]\),求出 \(\max\limits_{p\in [1, d]}\{a_{l_p} \oplus a_{r_p}\}\) 的值(\(\oplus\) 表示按位异或)。
相信大家都可以想到,维护两个单调栈 \(\operatorname {A,B}\),分别表示左边第一个比它大的和右边第一个比它小的的数的位置,于是一个区间 \([l,r]\) 是否合法的判定条件就是:
假如我们固定了其中一个端点,那么另外一个点的范围是可以通过这个得出的。
当然,因为 \(\operatorname {A,B}\) 数组并不满足单调性,所以不能直接进行求解。
那要怎么做呢?慢慢分析:
首先我们先固定左端点 \(l\),那么这个时候需满足区间右端点 \(r<\operatorname B_l\),并且固定了左端点以后你会发现,这个 \(\operatorname A\) 数组并没有什么用处,你可以用另外一个单调栈替换掉它,使得我们的做法更加简便。
我们在此重新定义 \(\operatorname A\) 表示右边第一个比自己大的数的位置。
样例的图示如下(其中以数的序号为横坐标,数值为纵坐标。蓝色的边是 \(\operatorname A\),红色的边是 \(\operatorname B\)):
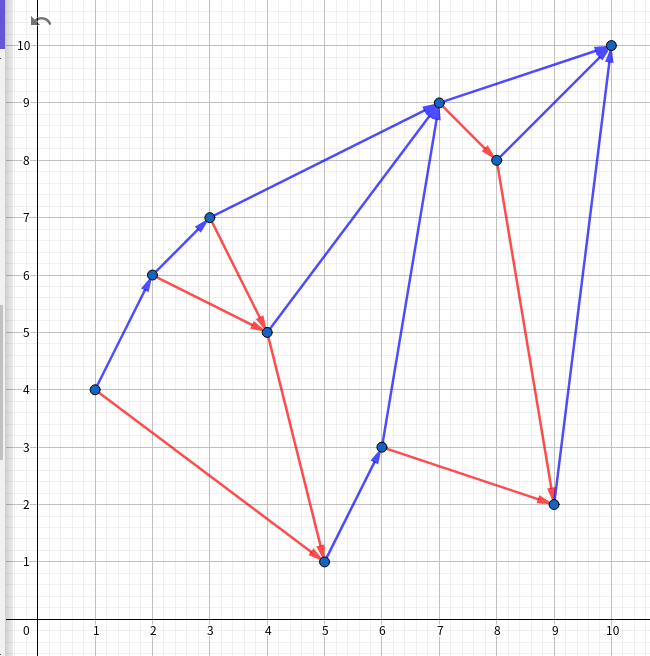
以下用 \(\min,\max\) 分别表示纵坐标最小的点和纵坐标最大的点。
假设我们钦定 \((1,4)\) 为左端点,即 \(\min\)。
那么区间的右端点的横坐标就不能超过 \(4\),因为点 \((5,1)\) 加入后会使得 \((1,4)\) 不能成为 \(\min\),与假设不符。
那么就从 \((1,4)\) 出发,沿着蓝边一直往上跳,只要横坐标还没超过 \(4\),路径上的点就都可以和点 \((1,4)\) 去更新一次答案。
很明显,所有的蓝边和红边各构成一片森林,最右边加个超级源点就是颗树。那么对于一个固定的左端点,所有可以符合的右端点,实际上就是一条树链。
处理异或用 Trie 树实现,但是由于每次需要调用一条树链上的数构成的 Trie 树,所以需要用到树上差分 \(+\) 可持久化 Trie 。
不会这个的不用慌,上网搜一下一看就会了。
_Wallace_ 说过,可持久化 Trie 树是最简单的可持久化了。
T4
子任务1-3
首先题意转化完就是维护一堆直线组成的下凸壳。
因为数据非常弱,答案最大好像也就只有 \(20\),暴力的复杂度和正解并没有区别。
子任务4-5
考虑每次加入一条直线 \(p\),它会和之前的直线有一些关系。
对于三种直线分开讨论:
- \(q_k<p_k\),即 \(p\) 的斜率更大,此时交点右边 属于 \(q\) 的部分会归属于 \(p\)。
- \(q_k=p_k\),此时这两条直线必然只会保留 \(b\) 值更大的那一条。
- \(q_k>p_k\),此时交点左边 属于 \(q\) 的部分会归属于 \(p\)。
那么就可以:
- 找到斜率等于自己的,判断是否需要替换。
- 找到斜率大于自己的,看能将对方的多少范围变成自己的,若是将对方所有都拿过来了,就可以把那条直线删掉,然后寻找重复本操作。
- 找到斜率小于自己的,同上。
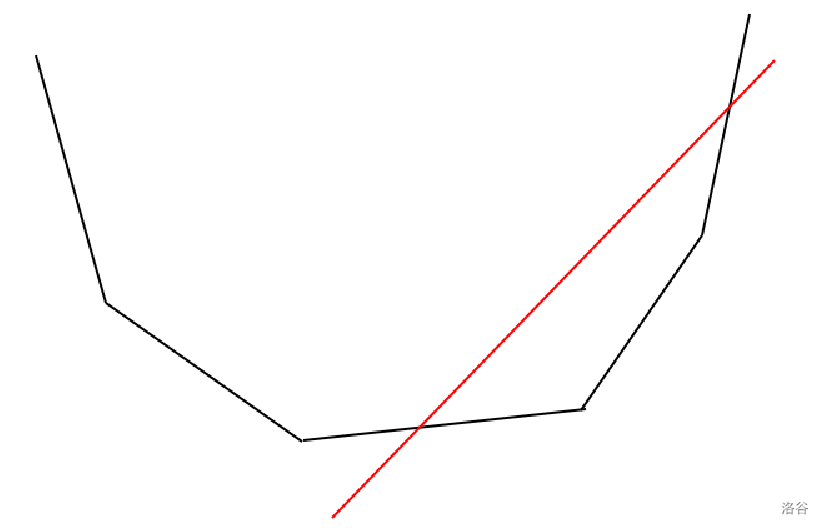
于是就可以用 set 维护这个凸包,查询前驱后继即可。
Part 2: std
(因为是 zjjws 写的解题报告所以 std 就放 zjjws 的了)
T1
#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int N=1e6+3;
int a[N];
int b[50];
int n,q;
LL rin()
{
LL s=0;
char c=getchar();
bool bj=0;
for(;(c>'9'||c<'0')&&c!='-';c=getchar());
if(c=='-')c=getchar(),bj=true;
for(;c>='0'&&c<='9';c=getchar())s=(s<<1)+(s<<3)+(c^'0');
if(bj)return -s;
return s;
}
int main()
{
int i,j;
n=rin();q=rin();
for(i=1;i<=n;i++)a[i]=rin();
for(;q>0;q--)
{
char x;
for(x=getchar();x!='Q'&&x!='M';x=getchar());
if(x=='Q')
{
int l,r;
l=rin();r=rin();
if(r-l+1>40){printf("Yes\n");continue;}
if(r-l+1<3){printf("No\n");continue;}
int ed=r-l;
for(i=l;i<=r;i++)b[i-l]=a[i];
sort(b,b+ed+1);
for(i=2;i<=ed;i++)if(b[i]<b[i-2]+b[i-1]){printf("Yes\n");break;}
if(i>ed)printf("No\n");
}
else
{
int p,c;
p=rin();c=rin();
a[p]=c;
}
}
return 0;
}
T2
#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int N=1e5+3;
const int Len=332;
const int K=332;
struct milk
{
int x,y;
bool z;
}a[N<<1];
int to[N];
LL num[N];
bool vit[N];
int n,T,M;
int now_m;
int sum_m;
int nam;
int x,s;
int ks;
LL ans;
struct cow
{
int l,r;
int lens;
int d[Len];
int cutt;
int tail;
bool if_true;
inline void build()
{
cutt=0;
tail=0;
for(int i=r;i>=l;i--)
if(vit[i]==true)
{
cutt++;
num[i]=(cutt<<1);
num[i]*=i;
}
for(int i=l;i<=r;i++)
if(vit[i]==true)
{
for(;tail>1;tail--)
{
if(num[i]>=num[d[tail]])continue;
if((num[d[tail]]-num[i])*(d[tail]-d[tail-1])<=(num[d[tail-1]]-num[d[tail]])*(i-d[tail]))continue;
break;
}
d[++tail]=i;
}
if_true=true;
return;
}
inline void cheak(LL cutt)
{
if(tail==0)return;
int L=2,R=tail;
int last=d[1];
for(;L<=R;)
{
int mid=(L+R)>>1;
if((cutt*(d[mid]-d[mid-1]))>=(num[d[mid-1]]-num[d[mid]]))last=d[mid],L=mid+1;
else R=mid-1;
}
ans=max(ans,cutt*last+num[last]);
return;
}
}t[K];
inline void work()
{
ans=0;
LL cutt=0;
for(int i=ks;i>0;i--)
{
if(t[i].cutt==0)continue;
if(!t[i].if_true)t[i].build();
if(((cutt+t[i].cutt)<<1)>now_m)
{
for(int j=t[i].r;j>=t[i].l;j--)
if(vit[j]==true)
{
cutt++;
LL ss;
ss=(cutt<<1)*j;
if((cutt<<1)>now_m)ss-=j;
ans=max(ans,ss);
if((cutt<<1)>=now_m)return;
}
return;
}
t[i].cheak(cutt<<1);
cutt+=t[i].cutt;
if((cutt<<1)>=now_m)return;
}
return;
}
inline void init()
{
int lens=sqrt(T);
ks=T/lens;
for(int i=1;i<=ks;i++)
{
t[i].l=t[i-1].r+1;
t[i].r=lens*i;
t[i].lens=lens;
t[i].if_true=false;
t[i].cutt=0;
for(int j=t[i].l;j<=t[i].r;j++)to[j]=i;
}
if(T%lens>0)
{
ks++;
int i=ks;
t[i].l=t[i-1].r+1;
t[i].r=n;
t[i].lens=t[i].r-t[i].l+1;
t[i].if_true=false;
t[i].cutt=0;
for(int j=t[i].l;j<=t[i].r;j++)to[j]=i;
}
return;
}
inline bool myru(milk x,milk y){return x.x<y.x;}
int rin()
{
int s=0;
char c=getchar();
bool bj=0;
for(;(c>'9'||c<'0')&&c!='-';c=getchar());
if(c=='-')c=getchar(),bj=true;
for(;c>='0'&&c<='9';c=getchar())s=(s<<1)+(s<<3)+(c^'0');
if(bj)return -s;
return s;
}
int main()
{
int i,j;
n=rin();T=rin();M=rin();
for(i=1;i<=n;i++)
{
int l,r,v;
l=rin();r=rin();v=rin();
a[i].x=l;a[i].y=v;a[i].z=true;
a[i+n].x=r+1;a[i+n].y=v;a[i+n].z=false;
}
init();
int m=(n<<1);
sort(a+1,a+m+1,myru);
j=1;
for(i=1;i<=T;i++)
{
now_m=rin();
for(;j<=m&&a[j].x==i;j++)
{
x=a[j].y;
vit[x]=a[j].z;
t[to[x]].if_true=false;
if(a[j].z==false)
{
t[to[x]].cutt--;
sum_m--;
}
else
{
t[to[x]].cutt++;
sum_m++;
}
}
now_m=min(now_m,sum_m);
if(now_m==0)
{
printf("0\n");
continue;
}
work();
printf("%lld\n",ans);
}
return 0;
}
T3
#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int N=5e5+3;
const int M=N<<5;
struct milk
{
int to[2];
int s;
inline void mem0(){to[0]=to[1]=s=0;return;}
}t[M<<1];
int a[N];
int b[N];
int d[N];
int A[32][N];
int B[N];
int st[N];
vector<int>to[N];
int n;
int nam;
int ans;
inline void make_tree(int now,int last,int s,int dp)
{
if(dp<0)return;
bool y=(s&(1<<dp));
t[now].to[y]=++nam;
t[nam].mem0();
t[nam].s=t[t[last].to[y]].s+1;
t[now].to[!y]=t[last].to[!y];
make_tree(t[now].to[y],t[last].to[y],s,dp-1);
}
inline void down(int x,int y,int s,int dp,int sum)
{
if(dp<0)
{
ans=max(ans,sum);
return;
}
bool k=(s&(1<<dp));
k=!k;
if(t[t[x].to[k]].s>t[t[y].to[k]].s)
{
sum+=(1<<dp);
down(t[x].to[k],t[y].to[k],s,dp-1,sum);
}
else
{
if(t[t[x].to[!k]].s>t[t[y].to[!k]].s)down(t[x].to[!k],t[y].to[!k],s,dp-1,sum);
else ans=max(ans,sum);
}
}
inline void work(int x,int y,int s)
{
x=st[x];y=st[y];
down(x,y,s,23,0);
}
inline void dfs(int x)
{
for(int i=0;i<to[x].size();i++)
{
int now=to[x][i];
nam++;
st[now]=nam;
t[nam].mem0();
make_tree(nam,st[x],a[now],23);
dfs(now);
}
if(x==n+1)return;
int y,s;
for(y=x,s=0;s>=0;)if(A[s][y]<B[x])y=A[s][y],s++;else s--;
work(A[0][x],A[0][y],a[x]);
}
int rin()
{
int s=0;
char c=getchar();
bool bj=0;
for(;(c>'9'||c<'0')&&c!='-';c=getchar());
if(c=='-')c=getchar(),bj=true;
for(;c>='0'&&c<='9';c=getchar())s=(s<<1)+(s<<3)+(c^'0');
if(bj)return -s;
return s;
}
int main()
{
// freopen("sample2.in","r",stdin);
int i,j;
n=rin();
int tail=0;
t[0].mem0();
for(i=1;i<=n;i++)
{
a[i]=rin();
for(;tail>0&&a[i]>a[d[tail]];tail--)A[0][d[tail]]=i,to[i].push_back(d[tail]);
d[++tail]=i;
}
for(;tail>0;tail--)A[0][d[tail]]=n+1,to[n+1].push_back(d[tail]);
for(i=1;i<=n;i++)
{
for(;tail>0&&a[i]<a[d[tail]];tail--)B[d[tail]]=i;
d[++tail]=i;
}
for(;tail>0;tail--)B[d[tail]]=n+1;
A[0][n+1]=n+1;
for(i=1;(1<<i)<=n;i++)
{
A[i][n+1]=n+1;
for(j=1;j<=n;j++)A[i][j]=A[i-1][A[i-1][j]];
}
// puts("true");
dfs(n+1);
// puts("true");
tail=nam=0;
t[0].mem0();
for(i=1;i<=n;i++)b[i]=a[i],to[i].clear();to[n+1].clear();
memset(st,0,sizeof(st));
for(i=1;i<=n;i++)
{
a[i]=b[n-i+1];
for(;tail>0&&a[i]>a[d[tail]];tail--)A[0][d[tail]]=i,to[i].push_back(d[tail]);
d[++tail]=i;
}
for(;tail>0;tail--)A[0][d[tail]]=n+1,to[n+1].push_back(d[tail]);
for(i=1;i<=n;i++)
{
for(;tail>0&&a[i]<a[d[tail]];tail--)B[d[tail]]=i;
d[++tail]=i;
}
for(;tail>0;tail--)B[d[tail]]=n+1;
A[0][n+1]=n+1;
for(i=1;(1<<i)<=n;i++)
{
A[i][n+1]=n+1;
for(j=1;j<=n;j++)A[i][j]=A[i-1][A[i-1][j]];
}
// puts("true");
dfs(n+1);
printf("%d\n",ans);
return 0;
}
T4
#include <cstdio>
#include <set>
#include <algorithm>
#define LL long long
using namespace std;
const int N = 1e6 + 3;
const LL INF = 0x3f3f3f3f3f3f3f3f;
int n, m;
inline LL rin()
{
LL s = 0;
bool bj = false;
char c = getchar();
for (;(c > '9' || c < '0') && c != '-';c = getchar());
if (c == '-')bj = true, c = getchar();
for (;c >= '0' && c <= '9';c = getchar())s = (s << 1) + (s << 3) + (c ^ '0');
if (bj)s = -s;
return s;
}
struct gyq
{
LL k, b;
}a[N];
inline bool myru(gyq x, gyq y) { return (x.k == y.k) ? (x.b < y.b) : (x.k < y.k); }
int d[N];
int tail;
inline long double cheak(int x, int y) { return (long double)(a[x].b - a[y].b) / (a[y].k - a[x].k); }
struct zjj
{
mutable long double l, r;
mutable LL k, b;
zjj(long double _l=0,long double _r=0, LL _k=0, LL _b=0){
l=_l,r=_r,k=_k,b=_b;
}
inline void add(long double l_,long double r_)
{
if (l == INF) { l = l_;r = r_;return; }
if (l_ > l)r = r_;
else l = l_;
return;
}
bool operator<(const zjj &tp)const{
return k<tp.k;
}
};
set<zjj>q;
inline double cheak_(zjj x, zjj y) { return (long double)(x.b - y.b) / (y.k - x.k); }
inline void work()
{
LL k = rin(), b = rin();
zjj now(INF,-INF,k,b);
if (q.empty()) { now.l = -INF;now.r = INF;q.insert(now);return; }
set<zjj>::iterator i = q.lower_bound(now);
if (i != q.end() && (i->k == k))
{
if (i->b >= b)return;
now.l = i->l;now.r = i->r;
q.erase(i);
if (q.empty()) { q.insert(now);return; }
i = q.lower_bound(now);
}
if(i!=q.end()&&i!=q.begin())
{
long double mid = cheak_(now, (*i));
if(mid<=i->l)return;
}
if(i!=q.end())
for (;true;)
{
long double mid = cheak_(now, (*i));
if (mid >= i->r)
{
now.add(i->l, i->r);
q.erase(i);
if (q.empty()) { q.insert(now);return; }
i = q.lower_bound(now);
if (i == q.end())break;
}
else { if (mid >= i->l) { now.add(i->l, mid);i->l = mid; }break; }
}
if (q.empty()) { now.l = -INF;if(now.r!=-INF) q.insert(now);return; }
i = q.lower_bound(now);
if (i == q.begin()) { now.l = -INF;if(now.r!=-INF)q.insert(now);return; }
i--;
for (;true;)
{
long double mid = cheak_(now, (*i));
if (mid <= i->l)
{
now.add(i->l, i->r);
q.erase(i);
if (q.empty())break;
i = q.lower_bound(now);
if (i == q.begin())break;
i--;
}
else { if (mid <= i->r) { now.add(mid, i->r);i->r = mid; }break; }
}
if (now.l < now.r)q.insert(now);
return;
}
int main()
{
int i;
n = rin();m = rin();
for (i = 1;i <= n;i++)a[i].k = rin(), a[i].b = rin();
sort(a + 1, a + n + 1, myru);
for (i = 1;i <= n;i++)
{
for (;i < n && a[i + 1].k == a[i].k;i++);
for (;tail > 1;tail--)if (cheak(i, d[tail]) > cheak(d[tail], d[tail - 1]))break;
d[++tail] = i;
}
printf("%d\n", tail);
for (i = 1;i <= tail;i++)
{
long double l = -INF, r = INF;
if (i != 1)l = cheak(d[i], d[i - 1]);
if (i != tail)r = cheak(d[i], d[i + 1]);
q.insert(zjj(l, r, a[d[i]].k, a[d[i]].b));
}
for (i = 1;i <= m;i++)
{
work();
printf("%lu\n",q.size());
}
return 0;
}
Part 3 个人评价:
T1
有一定的思维量。
T2
本身并没有考分块的意思,只是随便口胡了个题目,然后发现根号算法十分的优秀。据 serverkiller 说这题的平衡树解法常数巨大,甚至跑不过暴力,应该没有人会在考场上打平衡树的吧。当然我个人认为这题的考点不在于维护用的数据结构,而是如何特殊问题一般化,以及用斜率去优化。
部分分给的也挺足的,前 \(60\) 分可以轻松拿到。
T3
虽然是我出的,但是还是基本靠 _Wallace_ 搞出的正解。
思维量的话放在最后一题也不算太水,代码量还是很良心的。
T4
这道题因为只询问一次,那么就可以先将直线按斜率排一下序,然后在栈内维护凸壳。
我一开始没想到这个,于是糊了一个不用离线的做法,就有了这道题。
这么水的模拟题相信大家都 AK 了吧
Witten by @zjjws


