【读书报告--02】神经网络基础学习

1.线性单元

定义：使用一个可导的线性函数来替代感知器的阶跃函数，这种感知器就叫做线性单元

个人理解：感知器还是那个感知器，只是激活函数变成一个可导的线性函数：如f（x）=x

如下图：线性单元与前面所学的感知器（使用阶跃函数）的对比，只有激活函数改为”可导的线性函数“

2.监督学习和无监督学习的概念

监督学习：为了训练一个模型，我们要提供这样一堆训练样本：每个训练样本既包括输入特征x，也包括对应的输出y(也叫做标记，label)

无监督学习：训练样本中只有x而没有y

目前只考虑监督学习：

其中监督学习的所有样本误差的和函数为：

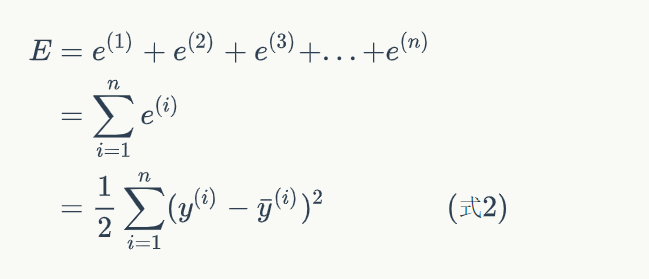
其中：

 

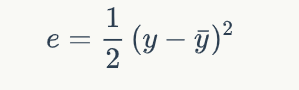
所以可以写成

 

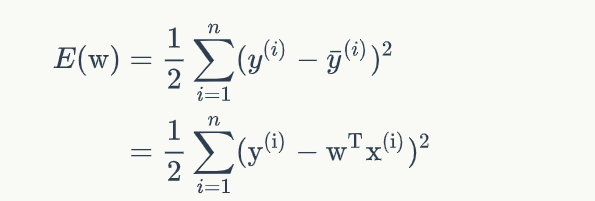
 由公式可知：模型的训练，实际上就是求取到合适的w，使(式2)取得最小值。这在数学上称作优化问题，而E（W）就是我们优化的目标，称之为目标函数

 个人理解：模型的训练是求取到合适的w，而通过观察误差和函数，实际上模型的训练的过程即对E(w)求取最小值，因此可以通过梯度下降算法优化我们的模型

3.梯度下降算法　　

公式和介绍：

因此我们的E(w)可以套入梯度下降的算法，对于神经网络模型训练的权值w

我们可以写出：

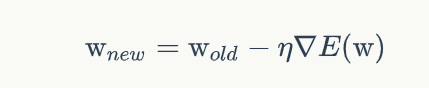
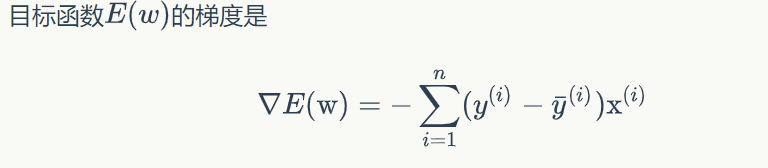
最终：

 

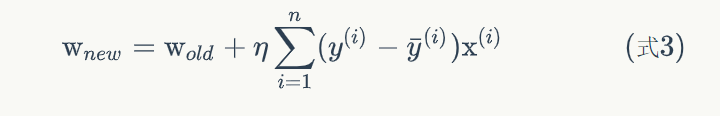
个人见解：

与上一节的感知器学习对比，权重w的训练更新公式替换成了如上图所示的公式，这样可以更快地训练出合适的w

 

总结：1.使用”可导的线性函数“作为感知器的激活函数，此时感知器叫做“线性单元”

2.监督学习和无监督学习的区别在于训练样本有无y，即实际值

3.梯度下降的算法可以优化神经网络模型，具体使用在对权值w的训练上