光速阅读Applied Linear Regression 4th

 

 前言：本书为声望较高的线性回归分析教材，且易自学。因找不到翻译版，故嗯读英文原版。

 同时结合配套资源 1 作者网站（http://users.stat.umn.edu/~sandy/alr4ed/） 2 线性代数基础

本书下载链接（https://www.pdfdrive.com/applied-linear-regression-e165850875.html）

 

 

正文：C H A P T E R 1 Scatterplots and Regression

散点图和回归函数

1. 认识散点图，简单。散点（plots）一般表示predictor variable（先入为主视为自变量x）和response variable（因变量y）。文中给出母女身高关系的例子，启示散点图可以有多种形式，通过round（四舍五入）来在一个range中分布plots，为了避免重复点使用jitter的方式。也可以把点分为不同trips（区）。

    

    

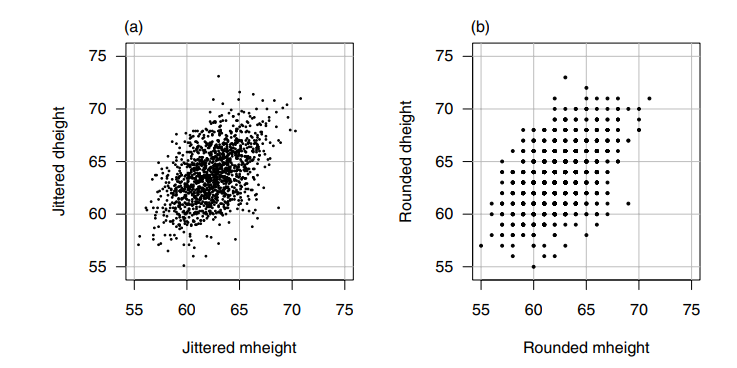
2. 特殊点处理，不可避免存在outlier和leverage的偏离函数方程的点，函数方程根据大多数点来拟合，所以这些点的特征是偏离大多数数据，处理按需去留。
3. 函数方程，分为非参数和参数方程，被称为mean function  E（x）的双参数和三参数。

    

   

    

    

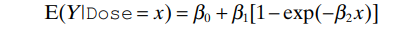
4. 方差在分析函数可以先默认为常数

    

    

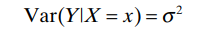
5. nonparametric estimated mean function（非参数方程）又称为smoother。一般取每个y的平均点拟合。
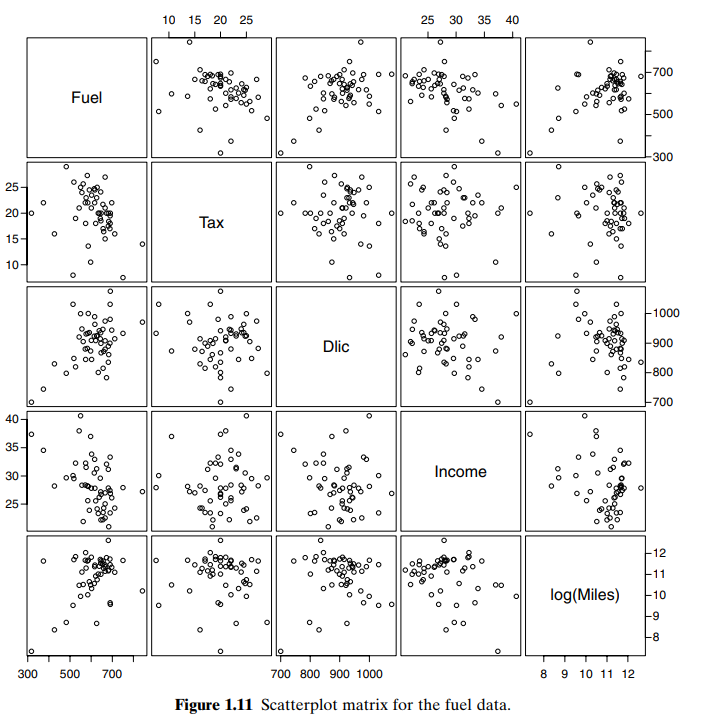
6. SCATTERPLOT MATRICES（散点矩阵），对一个自变量（population）多个因变量的多个散点图。本书给出美国各州燃油消耗量 收入 税收等因变量和人口自变量的例子，考虑到各州的人口基数不同，因变量自带（/每人）。
7.