拓扑排序
拓扑排序
闲谈
原因
唔,为了NOIP,加油(*´゚∀゚`)ノ
背景
拓扑排序我第一遍学的时候就模棱两可的,糊弄糊弄过去的,咳。后来做题的时候才发现缺点啥都不行 ̄へ ̄,于是又自学了一遍,写一篇博客来让自己更好的理解。
拓扑排序
背景
我至今还不太清楚他这个算法的名字-_-||(希望有大佬能告诉我)。首先我们需要了解一下这个算法是用来干什么的,一般在一些工程当中,我们需要完成若干个子工程来组成完整的工程,但是这些子工程之间存在着先后关系,也就是说存在着依赖关系,只有完成了一些工程才能够完成的后面的工程;这时候我们用一个有向图来表示工程之间的关系,子工程作为顶点,活动之间的先后关系为有向边,注意这里我们把这种有向图称为顶点表示活动的网络,又称为\(AOV\)网。
分析
好,那我们的目的就是解决这样一个建立在\(AOV\)网上的问题,我们这样定义:在\(AOV\)网中,如果有一条从顶点\(Vi\)到\(Vj\)的路径,那么我们就说\(Vi\)是\(Vj\)的前驱,\(Vj\)是\(Vi\)的后续。如果有弧\((Vi, Vj)\),那么我们就说\(Vi\)是\(Vj\)的直接前驱,\(Vj\)是\(Vi\)的直接后续。这些定义了解一下就可以,不需要单独的去背,最重要的是学会掌握如何使用他们。拓扑排序就是可以求出这些顶点先后遍历顺序的一种算法。
拓扑排序呢就是首先把\(AOV\)网中的所有顶点排成一个线性序列,如果有弧\((Vi, Vj)\),那么在这个序列当中\(Vi\)就要处于\(Vj\)的前面。
我们在这里需要引入一个概念在代码中表现为数组的形式来判断这个顶点是否可以进行,叫做入度指的是指向这个顶点的边有多少个,每当我们进行程序段时候,都是首先将入度为\(0\)的顶点输出,并且将它所指向的顶点的入度减一,这样就可以实现拓扑排序的过程了,在这个过程中我们需要使用到的是队列这种数据结构,可以让我们做到取队头插入队列称操作。
我认为拓扑排序的过程可以分为以下三步:
1、从图中选择一个入度为\(0\)的顶点输出。
2、从图中删除该顶点及所有指向的边(即与之相邻的所有顶点的入度减一)。
3、反复执行上面两个步骤,直到整个拓扑排序完成(如果没有入度为\(0\)的点了,那么说明图中存在环无解)。
具体例子
看例子才是最直观的能够理解一个问题的方法。我们来看这样一个场景。
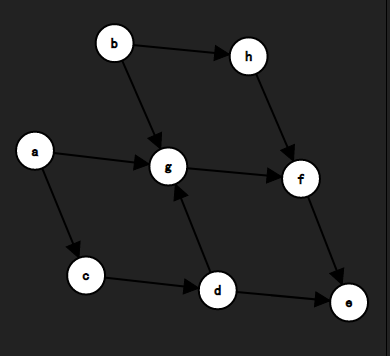
开始时,我们可以看到有\(a、b\)两个点的入度均为\(0\),那么我们随便选择一个输出,在这里我们选择\(b\),并删除\(b\)顶点及其所指向的边。
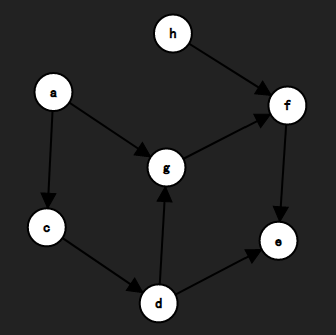
这时我们可以看到\(h\)的入度也为\(0\)了,我们再在它和\(a\)当中选择一个删去,再进行上面的步骤直至所有顶点均被删除。
代码实现
#include<queue>
#include<vector>
#include<cstdio>
#define N 10010
using namespace std;
int n, m, cnt = 0;
int head[N], in[N];
queue<int> q;
vector<int> qq;
struct edge{
int next, to;
}e[N << 1];
void add(int u, int v){
e[++cnt].next = head[u];
e[cnt].to = v;
head[u] = cnt;
}
void sort(){
int tot = 0;
for(int i = 1; i <= n; i++)
if(in[i] == 0) q.push(i), qq.push_back(i);
while(!q.empty()){
int u = q.front();
q.pop();
for(int i = head[u]; i; i = e[i].next){
int v = e[u].to;
in[v]--; //将连接入度减一
if(in[v] == 0){ //如果入度为0那么就输出
q.push(v);
qq.push_back(v);
}
}
}
}
int main(){
scanf("%d %d", &n, &m);
for(int i = 1; i <= m; i++){
int u, v; scanf("%d %d", &u, &v);
add(u, v);
in[v]++; //这就是用来记录入度的
}
sort();
for(int i = 0; i < qq.size(); i++)
printf("%d ", qq[i]);
return 0;
}
完结撒花ヾ(✿゚▽゚)ノ


