最小生成树

最小生成树\((MST)\)

闲谈

原因

又是蒟蒻的一篇为了记忆写的博客，扎实知识点。

背景

很多图论的题目会首先要求我们将图转化成树状结构再进行一系列的操作，而在这篇文章当中我将会介绍一种最常见的算法\(Kruskal\)来解决最小生成树这个问题。

\(Kruskal\)

背景

\(Kruskal\)作为最经典的最小生成树算法，在稍微改动后也可以求出最大生成树。是由\(Joseph Bernard Kruskal\)发明的，它的时间复杂度为\(O(elog_2e)\)，适合疏松图的最小生成树。

分析

\(Kruskal\)的思路为：假设连通网\(G=（V，E）\)，令最小生成树的初始状态为只有\(n\)个顶点而无边的非连通图\(T=（V，{}）\)，图中每个顶点自成一个连通分量。在\(E\)中选择代价最小的边，若该边依附的顶点分别在\(T\)中不同的连通分量上，则将此边加入到\(T\)中；否则，舍去此边而选择下一条代价最小的边。依此类推，直至\(T\)中所有顶点构成一个连通分量为止。我们用比较正常的方法来(翻译)一遍。首先我们需要一个前置技巧：并查集。

并查集

并查集并不是本篇文章的重点，只将简单介绍它的用法和基本思想。并查集是一种可以快速的求出每个节点所在的集合的数据结构，我们首先用数组\(fa[N]\)来记录它隶属哪个集合，第一步是初始化，将每一个节点的所在集合定义为它自己\(fa[i] = i\)我们用一个\(find\)函数来进行查找的工作

int find(int x){
	if(x != fa[x]) fa[x] = find(fa[x]);
	return fa[x];
}

通过这个操作我们就可以求出它所在的集合了，如果想要将两个节点所在的集合合并的话，那么就将第一个节点的\(fa\)值设为第二个节点的值即可。

我们回归到正题\(Kruskal\)，\(Kruskal\)算法是根据边的权值用递增的方式，一次找出边权值最小的边来建立最小生成树，并且每次所添加的边不能造成生成树的回路，这就需要我们刚才提到的并查集来做到了，直到找到第\(N - 1\)个边为止。
我们来看一个具体例子来更好的理解

我们首先将图中所有的边权快排。
首先将最短的边\((1, 3)\)加入生成树中

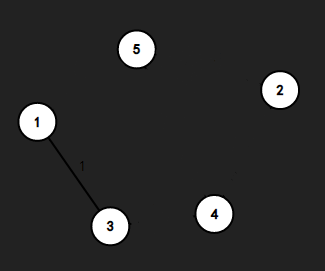
第二步将\((3, 4)\)加入生成树中

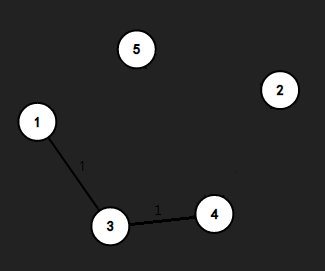
第三步将\((3, 5)\)加入生成树中

注意接下来的一部非常关键，需要我们之前提到的并查集来实现，我们发现如果按照边权来添加的话，应该添加的边为\((4, 5)\)但是我们发现\(4\)和\(5\)已经都被加入到生成树当中了，所以我们将其跳过添加\((4, 2)\)

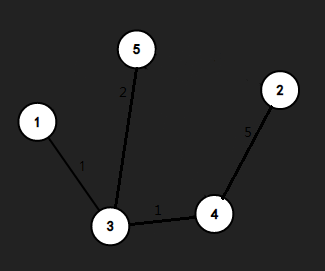
这时，我们已经建立了\(4\)条边，程序结束。
在进行每次加边时，我们需要考虑

\[1、它是否是剩下的边中最小的 2、加入它是否会生成环\]

代码实现

#include<cstdio>
#include<iostream>
#include<algorithm>
#define N 100010
using namespace std;
int n, m, ans = 0, cnt = 0;
int head[N], fa[N];
struct edge{
	int u, v, w;
}e[N << 1];
inline int read(){
	int s = 0;
	char ch = getchar();
	while(ch < '0' || ch > '9') ch = getchar();
	while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0'; ch = getchar();}
	return s;
}
bool cmp(edge a, edge b){return a.w < b.w;}
int find(int x){	//!!!非常重要,并查集模板 
	if(x != fa[x]) fa[x] = find(fa[x]);
	return fa[x];
}
void Kruskal(){	//Kruskal模板 
	sort(e + 1, e + m + 1, cmp);
	for(int i = 1; i <= n; i++) fa[i] = i;
	for(int i = 1; i <= m; i++){
		int x = find(e[i].u), y = find(e[i].v);
		if(x == y) continue;	//如果两条边已经联通那么跳过 
		ans += e[i].w;
		fa[x] = y;	//将两个点合并 
		if(++cnt == n - 1) break; //当n - 1条边时结束 
	}
}
int main(){
	n = read(); m = read();
	for(int i = 1; i <= m; i++){
		int x, y, z; 
		x = read(); y = read(); z = read();
		e[i].u = x; e[i].v = y; e[i].w = z;
	}
	Kruskal();
	printf("%d\n", ans);
	return 0;
}

我们来模拟一遍这个图。

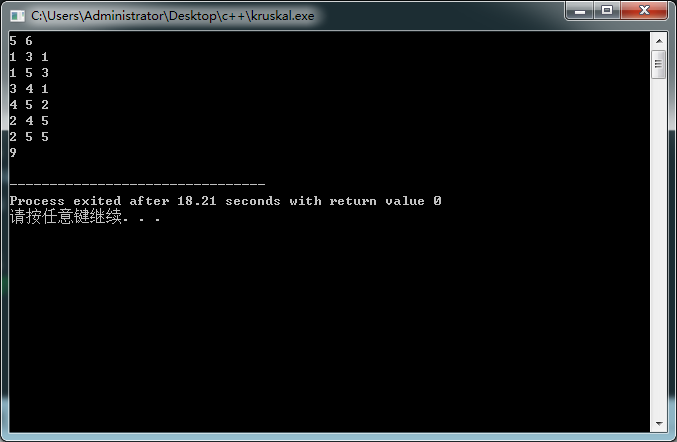
很明显，得出了正确的答案。那么这就是\(Kruskal\)算法，我们要灵活的应用它，有时我们需要求最大生成树，我们只要反着排序就可以了。
完结撒花ヾ(✿ﾟ▽ﾟ)ノ