最短路问题(2)
最短路问题\((2)\)
闲扯
原因
同上一篇(\(懒得打字了\))。
背景
在图论题当中,我们有时会遇到负权边,在这时我们之前提到过的\(Dijkstra\)就无法发挥作用了,我们来看这样一个简单的场景。
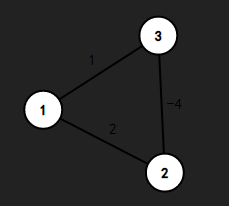
我们从点\(1\)出发,我们在循环的时候会将点\(3\)先标记上,这样\(dis[3] = 1\),但是我们明显可以观察得出,最短的路径应该是\(1\rightarrow2\rightarrow3\)应该\(dis[3] = -2\),但是此时我们已经把点\(3\)标记上了,所以不可以再进行修改,也就会得出错误的答案。这时,就需要一种可以处理负权边的算法了。
\(Bellman-Ford\)
背景
(不是要说\(SPFA\)嘛划去),其实对于负权边的图,最开始出现的算法是\(Bellman-Ford\),一会再谈\(SPFA\),因为\(SPFA\)都是基于\(Bellman-Ford\)上通过优化而得出的,我们首先要对\(Bellman-Ford\)有一个了解。\(Bellman-Ford\)是由\(Richard Bellman\)和\(Lester Ford\)两位大神创造的,因此得名。
分析
\(Bellman-Ford\)的百度解释如下(看看即可,反正也看不明白ヽ(ー_ー)ノ):对于给定的带权(有向或无向)图\(G = (V, E)\), 其源点为\(s\),加权函数\(w\)是边集\(E\)的映射。对图\(G\)运行\(Bellman - Ford\)算法的结果是一个布尔值,表明图中是否存在着一个从源点\(s\)可达的负权回路。若不存在这样的回路,算法将给出从源点\(s\)到图\(G\)的任意顶点\(v\)的最短路径\(d[v]\)。我的理解是将\(Bellman-Ford\)算法分为三个阶段:首先是要初始化,将除了起点之外的顶点的最短距离设为无穷大\(d[i] = +\infty, d[0] = 0\);下一步是迭代求解,反复的对每条边进行松弛(松弛指的是将所推出来的权值与到这个点原来的权值做对比,取小的),使每个顶点的最短距离\(d[i]\)估计值逼近最短距离(运行\(n - 1\)次);最后一步则是要检验负权回路,通过松弛的操作来判断每一条边的两个端点是否收敛,如果存在的话,那么说明存在负权回路返回\(false\),否则的话返回\(true\)并输出\(d[i]\)。我们可以得出\(Bellman-Ford\)的时间复杂度为\(O(VE)\),\((V为节点数,E为边数)\)。
具体例子
我们来看这样的一个图。
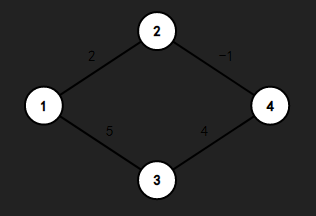
在这个例子中,我们设\(w[i, j]\)为各个顶点之间的距离,我们先用邻接表来表示。
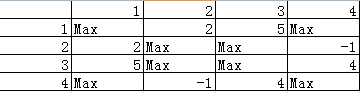
我们设\(d[i]\)为从点\(1\)至点\(i\)的最短路径,并将它们初始化\(d[i] = +\infty, d[0] = 0\)。
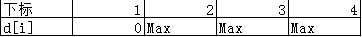
(1)第一步求\(d[2]\)的值\(d[1] + w[1, 2] < d[2] + w[2, 2] < d[3] + w[3, 2] < d[4] + d[4, 2];\)所以我们得出\(d[2] = d[1] + w[1, 2] = 2;\)。
(2)第二步求\(d[3]\)的值\(d[1] + w[1, 3] < d[2] + w[2, 3] < d[3] + w[3, 3] < d[4] + d[4, 3];\)所以我们得出\(d[3] = d[1] + w[1, 3] = 5;\)。
(3)第二步求\(d[4]\)的值\(d[2] + w[2, 4] < d[1] + w[1, 4] < d[3] + w[3, 4] < d[4] + d[4, 4];\)所以我们得出\(d[2] = d[1] + w[1, 2] = 1;\)。

可以看出,我们一共进行了\(3\)次松弛操作。
接下来继续进行松弛操作来检查是否存在负权边,若果发现\(d[i]\)的值变小,那么说明存在负权边并退出,否则的话就输出最短路径。显然我们可以看出\(d[4] + w[4, 2] < d[4]\),说明存在负权边。
优化
我们来分析一下\(Bellman-Ford\)算法,可以看出最外层的循环迭代次数为\(n - 1\)次,但实际上,如果不存在负权回路,最外层的循环次数应该远小于\(n - 1\)。我们来思考,在一次迭代当中,如果松弛的操作未被执行,那么说明在这次迭代当中所有的边都没有被松弛,这就说明任意的两点之间的距离在以后的迭代中不会再可能被缩小了,因此,迭代过程应该被提前结束。在这里我们可以设置一个\(bool\)型变量\(relaxed\),初始值为\(false\),如果在一次迭代过程中,有边被成功松弛,那么价格\(relaxed\)设置为\(true\),否则的话说明没有执行松弛操作,我们就可以结束外层循环。
bool Bellman_Ford_Plus(int x){
bool relaxed;
for(int i = 1; i <= n; i++) d[i] = Max;
d[x] = 0;
for(int i = 1; i < n; i++){
relaxed = false;
for(int j = 1; j <= n; j++)
for(int k = 1; k <= n; k++)
if(d[j] > d[k] + w[j][k]){
d[j] = d[k] + w[j][k];
relaxed = true;
}
if(!relaxed) break;
}
for(int i = 1; i <= n; i++) //判断是否有负环
for(int j = 1; j <= n; j++)
if(d[i] > d[j] + w[i][j])
return 1; //有负环
return 0; //无负环
}
\(SPFA\)
分析
终于到了今天的重头戏了,\(SPFA\)是基于\(Bellman-Ford\)的更进一步的优化,其时间复杂度一般情况下为\(O(kE)\),一般\(k \leq 2\)。\(SPFA\)和\(Bellman-Ford\)的实质都是更新最短路径的估计值,但是\(SPFA\)的关键在于:\(\textbf{只有那些在前一遍松弛过程中改变了距离估计值的点,才可能引起他们的临界点的距离估计值的改变}\)。
在编写代码时,我们是通过队列来实现这个操作的,首先将各个点的距离估计值设为\(+\infty\),并将起始点加入到队列当中。我们每次从队首取出一个点\(i\),遍历与\(i\)相联通的点\(j\),如果\(d[j] > d[i] + w[i][j]\),则需要进行松弛\(d[j] = d[i] +w[i][j]\),并将其存入最短路,并可以记录这个顶点进入进队次数来判断是否存在负环。直到队空的时候停止。
代码实现
我是以洛谷P3371 【模板】单源最短路径(弱化版)为原题做的模板。
#include<queue>
#include<cstdio>
#define INF 2147483647
using namespace std;
const int N = 500010;
int n, m, s, cnt = 0;
int head[N], dis[10010]; //dis记录到起点的长度
bool vis[N]; //vis记录是否在队
struct edge{
int to, next, w;
}e[N];
void add(int u, int v, int w){
e[++cnt].next = head[u];
e[cnt].to = v;
e[cnt].w = w;
head[u] = cnt;
}
void SPFA(){
for(int i = 1; i <= n; i++){
dis[i] = INF;
vis[i] = false;
}
dis[s] = 0; //起点到本身的距离为0
queue<int> q;
q.push(s); //起点入队
vis[s] = true;
while(!q.empty()){ //如果队列不为空
int u = q.front(); //取出队首
q.pop(); //将其弹出
vis[u] = false;
for(int i = head[u]; i; i = e[i].next){ //链式前向星遍历
int v = e[i].to;
if(dis[v] > dis[u] + e[i].w){ //松弛
dis[v] = dis[u] + e[i].w;
if(!vis[v]){ //如果没有入队
q.push(v);
vis[v] = true;
}
}
}
}
}
int main(){
scanf("%d %d %d", &n, &m, &s);
for(int i = 1; i <= m; i++){
int u, v, w; scanf("%d %d %d", &u, &v, &w);
add(u, v, w); //有向图, 无向加 add(v, u, w);
}
SPFA();
for(int i = 1; i <= n; i++)
if(s == i) printf("0 ");
else printf("%d ", dis[i]);
return 0;
}
我们模拟一下上面的图。
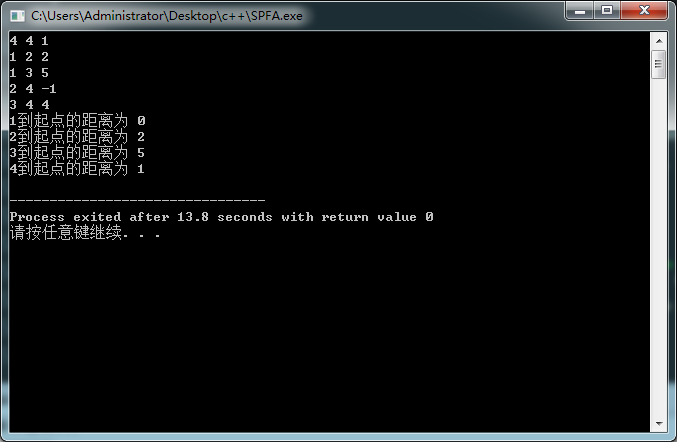
结果非常正确,得到了正确的算法。那么这就是\(Bellman-Ford\)和\(SPFA\)算法了,\(SPFA\)的速度非常快但是在算法竞赛中,如果是稠密图的话,出题人往往会卡常,(例如NOI2018D1T1),所以在为正权图时,还是要用\(Dijkstra\)算法,当出现负权图时我们就可以大胆的使用\(SPFA\)了。
完结撒花ヾ(✿゚▽゚)ノ


