几种分布

1.概率质量函数与概率密度函数
　　 在概率论中，概率质量函数 (Probability Mass Function，PMF)是离散随机变量在各特定取值上的概率。概率质量函数和概率密度函数不同之处在于：概率密度函数是对连续随机变量定义的，本身不是概率，只有对连续随机变量的取值进行积分后才是概率。
2.伯努利分布
　（1）伯努利试验：只有两种可能结果的单次随机试验
　（2）试验E是一个伯努利试验，将E独立重复地进行n次，则称这一串重复的独立试验为n重伯努利试验。
　（3）进行一次伯努利试验，成功(X=1)概率为p(0<=p<=1)，失败(X=0)概率为1-p，则称随机变量X服从伯努利分布，其概率质量函数为：
　　　　
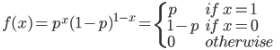
3 均匀分布
　　对于投骰子来说，结果是1到6。得到任何一个结果的概率是相等的，这就是均匀分布的基础。与伯努利分布不同，均匀分布的所有可能结果的n个数也是相等的。
如果变量X是均匀分布的，则密度函数可以表示为：

　　　　

　　均匀分布的曲线是这样的：

　　　　

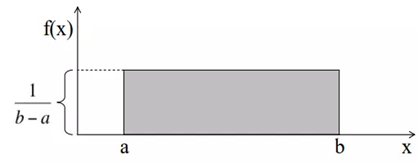
　　均匀分布曲线的形状是一个矩形，这也是均匀分布又称为矩形分布的原因。其中，a和b是参数。
4.二项分布
　　（1）二项分布(Binomial distribution)是n重伯努利试验成功次数的离散概率分布。
　　（2）如果试验E是一个n重伯努利试验，每次伯努利试验的成功概率为p，X代表成功的次数，则X的概率分布是二项分布，记为X~B(n,p)，其概率质量函数为：

　　　　

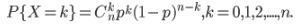
　　（3）伯努利分布是二项分布在n=1时的特例
　　（4）二项分布名称的由来，是由于其概率质量函数中使用了二项系数，该系数是二项式定理中的系数，二项式定理由牛顿提出：

　　　　

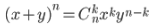
　　（5）总结二项式分布的属性：
　　　　1）. 每个试验都是独立的。
　　　　2）. 在试验中只有两个可能的结果：成功或失败。
　　　　3）. 总共进行了n次相同的试验。
　　　　4）. 所有试验成功和失败的概率是相同的。 （试验是一样的）
5.正态分布
　　（1）正态分布的特点：
　　　　1）. 分布的平均值、中位数和模式一致。
　　　　2）. 分布曲线是钟形的，关于线 x = μ 对称。
　　　　3）. 曲线下的总面积为1。
　　　　4）. 有一半的值在中心的左边，另一半在右边。
　　（2）概率密度函数：

　　　　

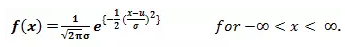
　　（3）均值和方差：
　　　　均值 -> E(X) = µ
　　　　方差 -> Var(X) = σ^2
6.多项分布
　　与二项分布不同的地方在于每次试验的结果有多个，所有结果互斥且概率和为1。
　　其概率质量函数为：

　　　　

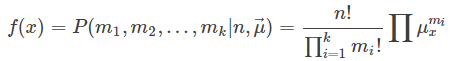
　　假设20%的萤火虫喜欢花粉，35%的萤火虫喜欢蚜虫，45%的萤火虫喜欢面团。我们对30只萤火虫做实验，发现8只喜欢花粉，10只喜欢蚜虫，12只喜欢面团，这件事的概率为 ：

　　　　

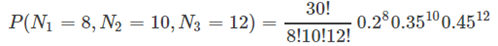
　　这时的参数μ变成了一个向量μ⃗ ={μ1,μ2,...,μk}表示第一个取值被选中的概率，这里为μ⃗ ={0.2,0.35,0.45}。在伯努利分布里，参数μ就是抛硬币取某一面的概率，因为伯努利分布的状态空间只有{0,1}。但是在多项分布里，因为状态空间有K个取值，因此μ变成了向量μ⃗ ={μ1,μ2,...,μk}。
7.Beta分布
　　Beta分布表示概率的分布。即不同于极大似然的观点，在Beta分布里，所有的事件发生的概率都不是固定的。Beta分布对于：我们事先不知道概率是什么但又有一些合理的猜测时，贝塔分布能够很好地表示为一个概率的分布，然后根据样本或者试验等新的信息，来修正概率的分布。
　　Beta的概率密度函数：

　　　　

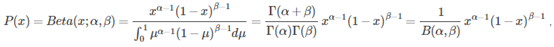
　　其中,

　　　　

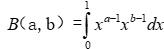
　　贝塔函数和伽马函数的关系：

　　　　

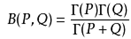
　　Beta分布的均值：

　　　　

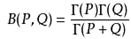
　　假设图形为：

　　　　

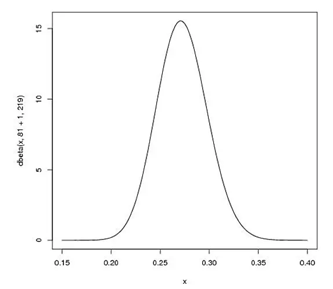
　　此图形仅仅是用作解释概率密度函数。其中横轴为概率x，纵轴为该概率的置信度（即Beta函数的值）。（置信度：如抛100次中，30次向上，和抛100000次中30000次向上，两者估计p的值都是0.3。但后者更有说服力。如果前者实验得到p为0.3的置信度是0.5的话，后者实验得到p为0.3的置信度就有可能是0.9，更让人信服）
　　在增加新的样本信息X（二项分布，下面的例子中假设二项分布中n=10,且I(x=1)=4)后，p的后验概率依然为Beta分布：

　　　　

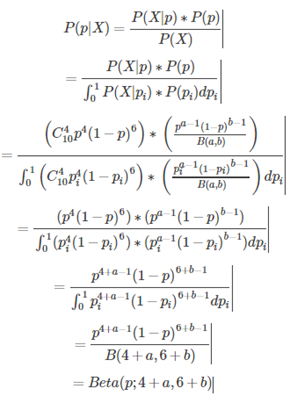
　　根据上面的结果可以发现，加入新的信息，并不改变原分布，只是将分布函数进行了平移和缩放。
8.狄里克雷分布
　　狄利克雷分布(Dirichlet distribution)是多项分布的共轭分布。
　　计算公式：

　　　　

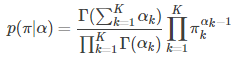
　　其类似于Beta分布的式子：

　　　　

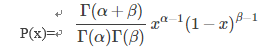
　　Beta分布是模型抛硬币为正的概率的分布，Dirichlet可以是掷骰子模型中的掷出来的点数的分布：
　　假设筛子各个面被掷中概率服Dirichlet(π|10,10,20,20,20,20))。现在又做了100次掷骰子实验，假设为1的次数是20，为2的次数是10，为3的次数是40，为4的次数是10，为5的次数是10，为6的次数是10。所以根据贝叶斯后验概率公式和多项式分布更新得到筛子个个面被掷中概率服从Dirichlet(π|(30,20,60,30,30,30))。
9.泊松分布
　　泊松分布是二项分布n很大而p很小时的一种极限形式。二项分布是说，已知某件事情发生的概率是p，那么做n次试验，事情发生的次数就服从于二项分布。泊松分布是指某段连续的时间内某件事情发生的次数，而且“某件事情”发生所用的时间是可以忽略的。
　　例如，在五分钟内，电子元件遭受脉冲的次数，就服从于泊松分布。假如你把“连续的时间”分割成无数小份，那么每个小份之间都是相互独立的。在每个很小的时间区间内，电子元件都有可能“遭受到脉冲”或者“没有遭受到脉冲”，这就可以被认为是一个p很小的二项分布。而因为“连续的时间”被分割成无穷多份，因此n(试验次数)很大。所以，泊松分布可以认为是二项分布的一种极限形式。
　　泊松分布的概率密度函数为：

　　　　

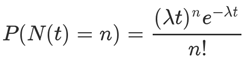
　　其中，P 表示概率，N表示某种函数关系，t 表示时间，n 表示数量，1小时内出生3个婴儿的概率，就表示为 P(N(1) = 3) 。
　　举例：假设已知：
　　某医院平均每小时出生3个婴儿。则：
　　接下来两个小时，一个婴儿都不出生的概率是0.25%，基本不可能发生：

　　　　

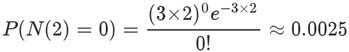
　　接下来一个小时，至少出生两个婴儿的概率是80%：
　　　　

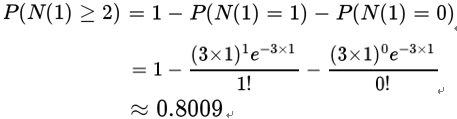
　　泊松分布的图形：

　　　　

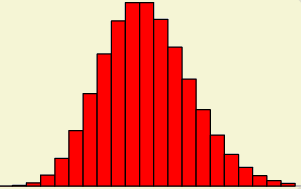
　　可以看到，在频率附近，事件的发生概率最高，然后向两边对称下降，即变得越大和越小都不太可能。每小时出生3个婴儿，这是最可能的结果，出生得越多或越少，就越不可能。
10.指数分布
　　指数分布是事件的时间间隔的概率。在一个时间段内事件平均发生的次数服从泊松分布，这个次数在泊松分布中用lambda表示。这个lambda在指数分布里面的意义基本是一样的，也是在一个时间段内事件平均发生的次数。泊松分布表示的是事件发生的次数，“次数”这个是离散变量，所以泊松分布是离散随机变量的分布。指数分布是两件事情发生的平均间隔时间，“时间”是连续变量，所以指数分布是一种连续随机变量的分布。可以用等公交车作为例子：某个公交站台一个小时内出现了的公交车的数量 就用泊松分布来表示某个公交站台任意两辆公交车出现的间隔时间 就用指数分布来表示
　　指数分布公式：
　　通过泊松分布来推导：同样使用医院的例子：如果下一个婴儿要间隔时间 t ，就等同于 t 之内没有任何婴儿出生。

　　　　

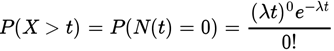
　　计算接下来15分钟，会有婴儿出生的概率是52.76%：

　　　　

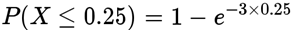
　　指数分布的图形：
　　　　

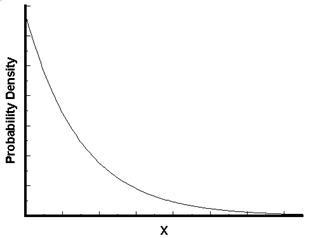
　　泊松分布和指数分布的前提是，事件之间不能有关联，否则就不能运用上面的公式。泊松分布是单位时间内独立事件发生次数的概率分布，指数分布是独立事件的时间间隔的概率分布。