sampling method

sampling method

背景

在贝叶斯框架下，利用后验分布对参数进行估计，也即

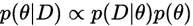
其中
（1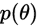）是参数的先验分布。
（2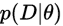）是似然分布，数据集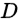的生成联合概率
（3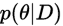）是参数的后验分布。

通常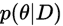分布很复杂，所以可以采用sampling方法从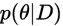中采样样本，表示后验分布。如计算参数的期望。

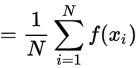
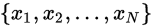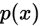其中是从中抽取的一组样本。

MCMC

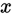马尔科夫蒙特卡洛方法（MCMC）是最常用的采样技术。其关键是通过构造平稳分布为的马尔科夫链，则此时产出的样本近似服从分布。

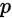平稳分布

设
（1）马尔科夫链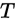的状态转移概率为。
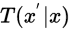（2）在时刻状态的分布为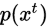
若此时

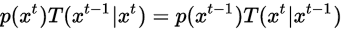
则马尔科夫链满足细致平稳条件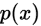，是该马尔科夫链的平稳分布。

Metropolis-Hasting算法

1. initialize
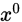
2. for i = 0 to N - 1
   
   
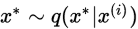
   if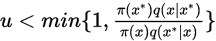
   
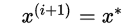
   else:
   

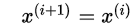
证明：

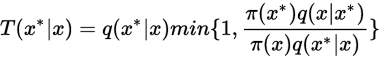
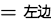
因此，满足细致平稳条件，且服从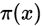
MH算法关键是选择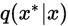，虽然理论上可以随便选。

Gibbs采样算法

gibbs主要用于对多维分布采样
initialize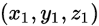

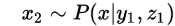
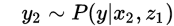
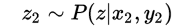
证明
由采样流程：

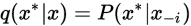
则代入MH

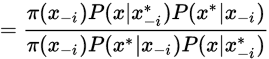
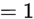
所以，gibbs是MH的一种特殊形式。