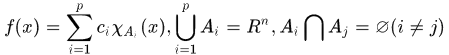实变函数论笔记
实变函数论
第二章 Lebesgue测度
2.1 点集的Lebesgue外测度
定义2.1 设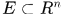 ,若
,若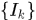 是
是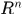 中可数个开矩体,且有
中可数个开矩体,且有
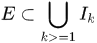
则称
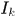 为E的一个L-覆盖。我们称
为E的一个L-覆盖。我们称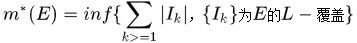
为点集
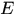 的Lebesgue外测度。
的Lebesgue外测度。若
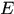 的任意的L-覆盖
的任意的L-覆盖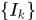 均有
均有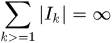
则
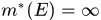 ,否则
,否则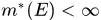
定理2.1 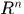 中点集的外测度性质
中点集的外测度性质
(1)非负性: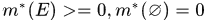
(2)单调性:若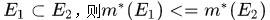
(3)次可加性: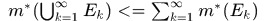
2.2 可测集与测度
定义2.2 设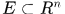 。若对任意的点集
。若对任意的点集 ,有
,有
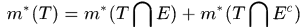
则称E为Lebesgue可测集,简称为可测集,其中
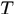 称为试验集
称为试验集
注:
(1)在证明时,我们只需要对任一点集 ,证明
,证明
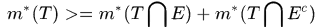
即可
(2)外测度为零的点集称为零测集。
定理2.6 可测集的性质
(1)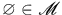
(2)若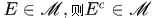
(3)若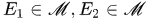 ,则
,则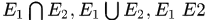 都属于
都属于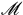
(4)若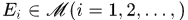 ,则其并集也属于
,则其并集也属于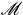 ,若进一步
,若进一步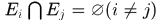 ,则
,则
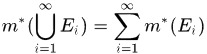
即
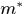 在
在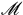 上满足可数可加性(或称为
上满足可数可加性(或称为 )
)
注
从定理的结论(1)(2)(4)可知,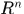 中可测集类构成一个
中可测集类构成一个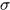 代数。对于可测集
代数。对于可测集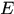 ,其外测度称为测度,记为
,其外测度称为测度,记为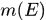 ,这就是通常所说的
,这就是通常所说的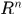 上的Lebesgue测度。
上的Lebesgue测度。
第三章 可测函数
3.1 可测函数的定义及其性质
定义3.1 设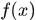 是定义在可测集
是定义在可测集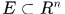 上的广义实值函数。若对于任意的实数
上的广义实值函数。若对于任意的实数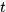 ,点集
,点集
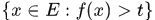
是可测集,则称
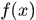 是
是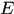 上的可测函数,或称
上的可测函数,或称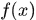 在
在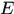 上可测
上可测
定理3.4 可测函数的运算性质:若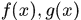 是
是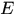 上的实值可测函数,则下列函数
上的实值可测函数,则下列函数
(1)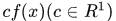
(2)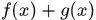
(3)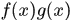
都是 上的可测函数。
上的可测函数。
定理3.6 可测函数的运算性质:若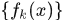 是
是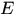 上的可测函数列,则下列函数
上的可测函数列,则下列函数
(1)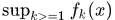
(2)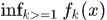
(3)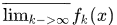
(4)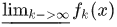
都是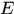 上的可测函数。
上的可测函数。
3.2 可测函数列的收敛
几乎处处收敛与一致收敛
定义3.5 设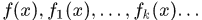 是定义在点集
是定义在点集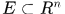 上的广义实值函数。若存在
上的广义实值函数。若存在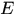 中的点集
中的点集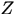 ,有
,有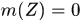 及
及
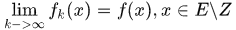
则称
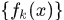 在
在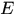 上几乎处处收敛于
上几乎处处收敛于 ,并简记为
,并简记为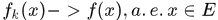
注 一致收敛:令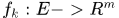 是一个函数列,并且,对于任意的
是一个函数列,并且,对于任意的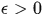 ,存在
,存在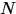 ,使得当
,使得当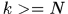 时,
时,
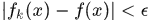
成立,则称
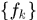 一致收敛到
一致收敛到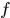 ,写作
,写作
几乎处处收敛与依测度收敛
定义3.6 设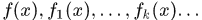 是
是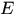 上几乎处处有限的可测函数,若对任意的
上几乎处处有限的可测函数,若对任意的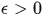 ,有
,有
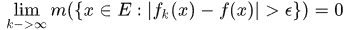
则称
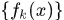 在
在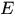 上依测度收敛于
上依测度收敛于
3.3 可测函数与连续函数
第四章 Lebesgue积分
非负可测函数的积分
定义4.1 设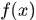 是
是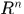 上的非负可测简单函数,它在点集
上的非负可测简单函数,它在点集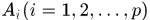 上取值为
上取值为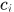 :
: