topic model

0、基石——贝叶斯推断

计算后验概率即为我们对参数的估计：

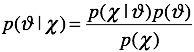
其中：

    ——输入数据

     ——待估计的参数

    ——似然分布

     ——参数的先验分布

 

对新样本的预测：我们要估计的概率

1、常用的概率分布

Dirichlet Distribution

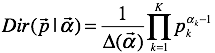
2、文本建模

2.1 基本模型——unigram model

最基本的一种文本模型。

我们做这样的假设：语料库是从词表中独立的抽取的个。有似然方程

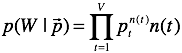其中是term[t]出现的次数。我们的目标是估计，根据贝叶斯推断的方法，我们需要引入的一个先验分布。

计算后验概率

至此，我们就得到的参数的在观测到输入语料库的条件下的概率分布。而这个参数确定了语料库生成模型——Unigram model。我们认为语料库是这样生成的：每篇文档的每个词都从同一个二项分布模型中sample得到。显然，这是不靠谱的。

3 LDA建模

3.1 图模型

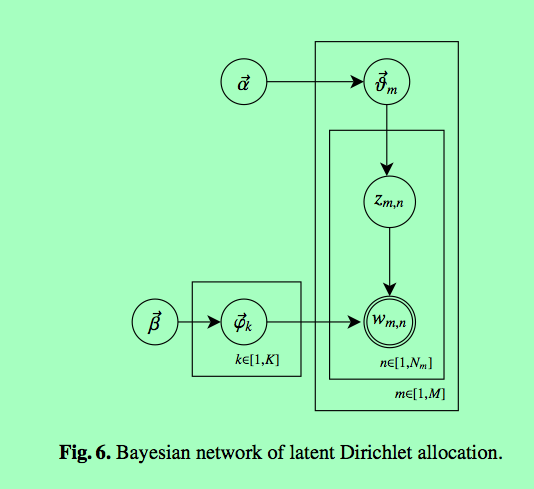
Lda的生成模型描述如下：模型随机出词的序列，分为一个个以文档为单位的词向量。对于每一个文档的每一个词，首先sample词的topic, 服从以为参数的多项分布；接着，sample每一个词 ，服从以为参数的多项分布，表示每一个topic下词的分布。

为了获得bayesian的生成模型，引入dirichlet分布， 、分别服从参数为和的dirichlet分布。

3.2 模型的推导

根据图模型的条件独立性，我们首先推导联合概率分布。

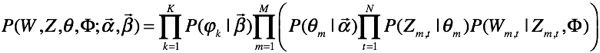
其中，为维参数， 为 维参数。

现在有两种方式进行推导，一种是采用变分的方法，另一种是采用gibbs采样。我们采用collapsed gibbs sampling方法来做这个问题。

首先对和积分，得到的联合分布：

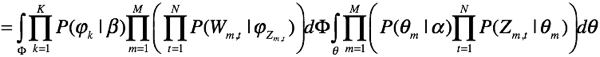
上式将二重不定积分分离为两个不相关的子积分，现在分别求这两个积分。

小做变换：

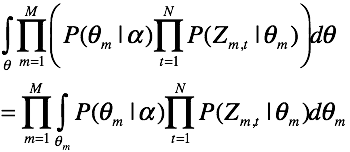
引入有用的符号：

表示第m篇文档中词汇r是由主题k生成的数量;

表示第m篇文档中由主题k生成的词的数量；

表示语料库中词汇r由主题k生成的数量；

求子积分式：

 

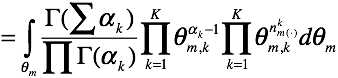
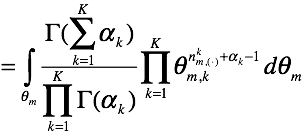
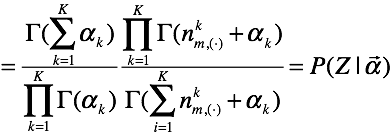另一式：

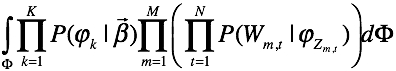
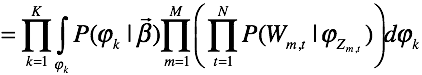推导每一个子式

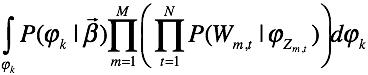
继续写下去，这里的意义有必要说明一下：由两个支路来产生我们的词，首先由产生每一个文档的每一个词的topic，然后根据每个topic生成词。

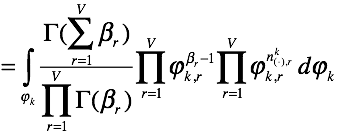
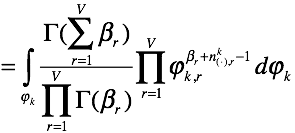
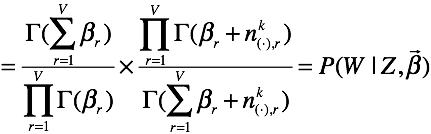 上面的推导就相当于，perfect！！我们就有了以下的式子：

 

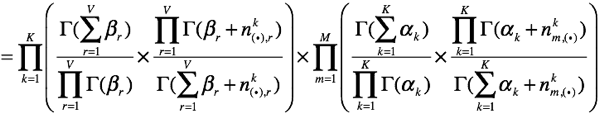
3.2 collapsed Gibbs sampling

在上述推导的分布中，是隐变量，是观测量。我们将 和两个变量积分掉，原因是我们可以从和的相互关系中推导出和。

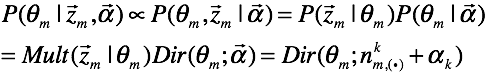
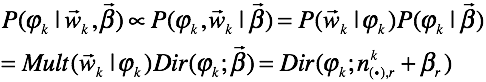
其中， 表示其topic为K的词的集合。因此，我们易得

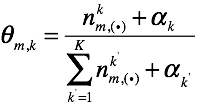
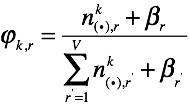（MCMC的一种理解）为什么我们现在有资本用以上两式来估计参数，就像混合高斯模型一样，对于每一篇文档我们有个参数，对于每个词，我们还是有个分布。我们利用MCMC来采样出隐变量，而在EM算法中我们求隐变量的后验概率。为什么我们用MCMC，因为隐变量的后验概率不是那么好求的。当然，我们可以用变分的方法，那就复杂了。通过前面的图模型，当我们知道了complete data。我们的theta和fi都可以inference，因为theta有先验，当我们知道数据之后，当然可以inference，这是bayes的思路，不需要像em一样，去最优化一个问题。 

有必要先简介一下MCMC和gibbs方法

对于一个高维分布，我们利用马尔科夫链的平稳性，经过一段“burn-in period”之后继续得到的数据服从这个分布。而gibbs方法是一种特例。

对于含有隐变量的联合分布，我们为了得到后验分布

a. 选择一个维度

b. sample from 

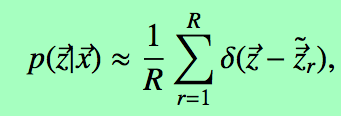对采样结果计数，估计条件分布律，基于这样的假设，我们得到了真正的数据。

明白了上面的问题，涉及我们怎么去解这个图模型的基本方法，我们去制造数据来inference。

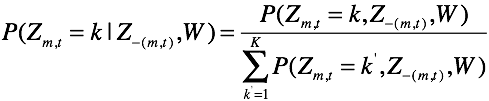其中，k=1,…,K，求这样一个分布律。

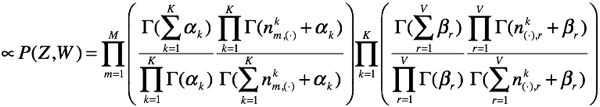
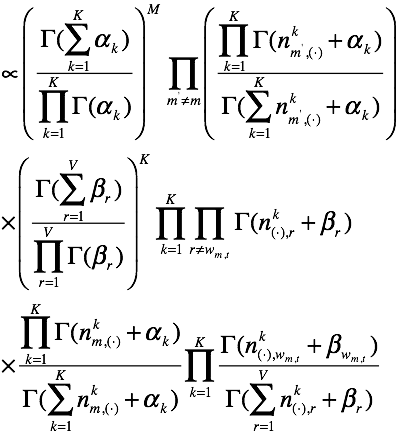
这一步，我们做的是将分子分母的公共项（不受影响的）提出来。接下类是分离k，直接给sample的式子。

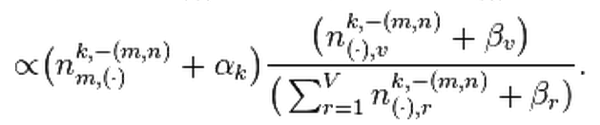其中， ； 表示计数中不能包含。