PLSA的EM推导
本文作为em算法在图模型中的一个应用,推导plsa的em算法。
1 em算法
em算法是解决一类带有隐变量模型的参数估计问题。
1.1 模型的定义
输入样本为![]() ,对应的隐变量为
,对应的隐变量为![]() 。待估计的模型参数为
。待估计的模型参数为![]() ,目标为极大化似然函数
,目标为极大化似然函数

对于上式的优化,不能通过直接对![]() 进行求导,因为一旦求导,就有如下的形式:
进行求导,因为一旦求导,就有如下的形式:
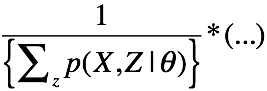
显然是不好求的。
1.2 em算法的迭代过程
a. 初始化:随机初始参数的![]()
b. E step:
计算隐变量的后验分布
![]()
c. M step:
迭代参数![]()
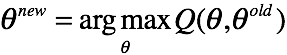
其中,Q函数为X,Z的对数联合分布在Z的后验分布下的期望
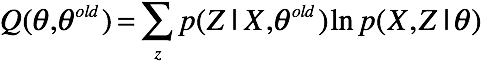 上面的式子,将样本和隐变量都表示成矩阵的形式,让人有些不太好套公式。
上面的式子,将样本和隐变量都表示成矩阵的形式,让人有些不太好套公式。
2 高斯混合模型
2.1 基本模型
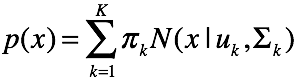 混合高斯模型认为,变量
混合高斯模型认为,变量![]() 服从一个多峰的高斯分布,由数个高斯分布组合而成。所以我们首先引入隐变量
服从一个多峰的高斯分布,由数个高斯分布组合而成。所以我们首先引入隐变量![]() ,并且我们认为变量
,并且我们认为变量![]() 通过这样一个过程生成。引入隐变量的高斯混合模型用图模型表示:
通过这样一个过程生成。引入隐变量的高斯混合模型用图模型表示:
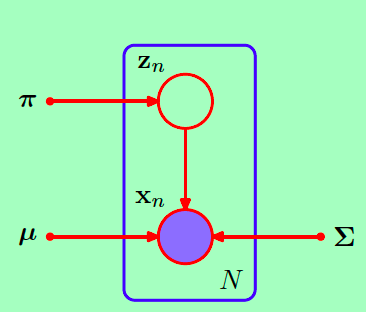
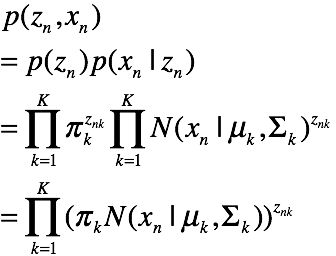
因此该图模型表示的联合概率为:
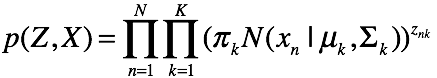 2.2 em算法的推导
2.2 em算法的推导
e step: 计算每一个样本的后验概率,遍历k等于1的各种情况
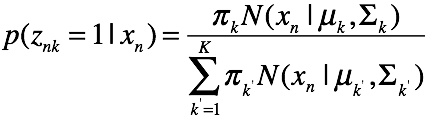
M step: 首先推导Q方程
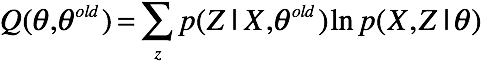
对于每一对![]()
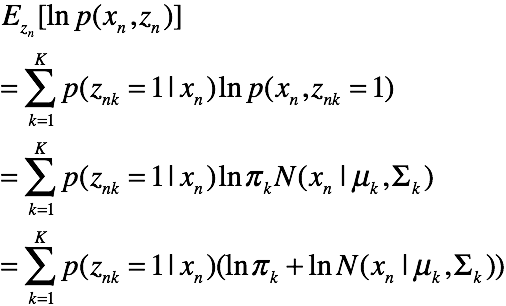
由于N个样本独立,所以有
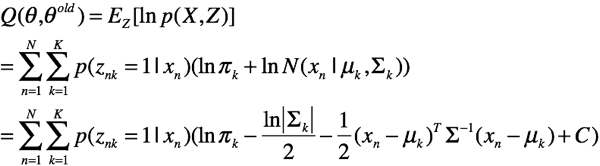
好了,我们开始极大化这个期望
求均值
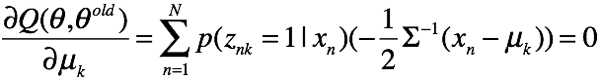 解方程得
解方程得
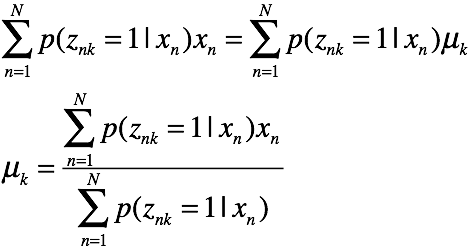
求方差比较复杂,直接给出结论:
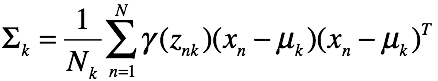
其中:
![]()
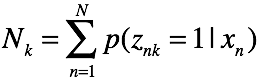 最后求
最后求![]() ,注意这里
,注意这里![]() 的概率和为1,用拉格朗日乘子法解受限优化问题。有拉格朗日函数
的概率和为1,用拉格朗日乘子法解受限优化问题。有拉格朗日函数
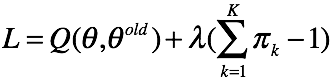
对 ![]() 求偏导有
求偏导有
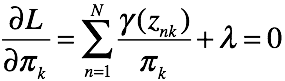
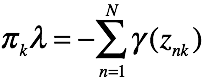
有k个关于![]() 的方程,对这些方程做累加有
的方程,对这些方程做累加有
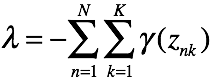
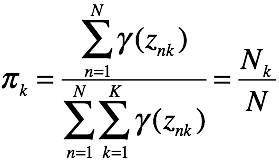 其中,
其中,![]() 是概率,对k的累加和为1
是概率,对k的累加和为1
至此,混合高斯模型的em迭代方法推导完毕,总结如下
E step:
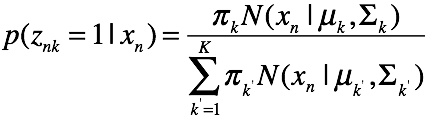
M step:
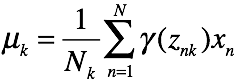
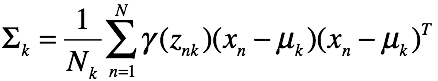
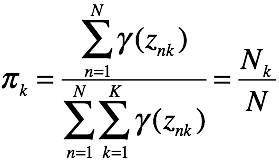
其中![]()
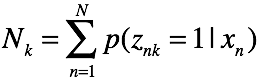
好了,我们完成了混合高斯模型的推导。混合高斯模型是一般高斯模型的推广,使得概率密度估计的外延得到扩展。另外,我们搞清楚了em算法使用的细节,在e step,我们求每一对(zn,xn)的后验概率和联合概率,遍历zn的所有情况,然后求每一个对数似然函数的期望,并在N上求和,就得到了目标函数。
3 PLSA主题模型
PLSA主题模型是比较老的模型了,逐渐被LDA这种更bayesian的方法取代了。我们来看看图模型。
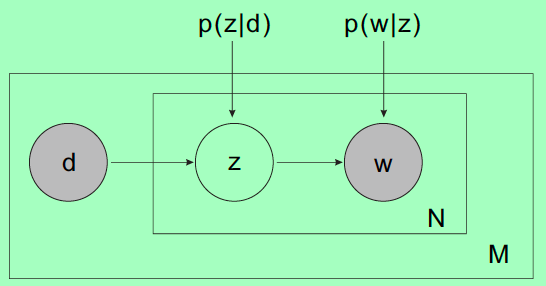
3.1 模型假设
对于一篇文档![]() ,在每一个词的位置,首先选择一个topic,然后在topic的词分布中选择一个词作为当前位置的词
,在每一个词的位置,首先选择一个topic,然后在topic的词分布中选择一个词作为当前位置的词![]() 。输入样本为
。输入样本为![]() ,需要估计的参数为
,需要估计的参数为![]() 在主题上的分布
在主题上的分布![]() ,以及主题下词的分布
,以及主题下词的分布![]() 。
。
首先求联合概率。对于![]() 这一Complete样本,
这一Complete样本,
有联合概率
![]()
有后验概率
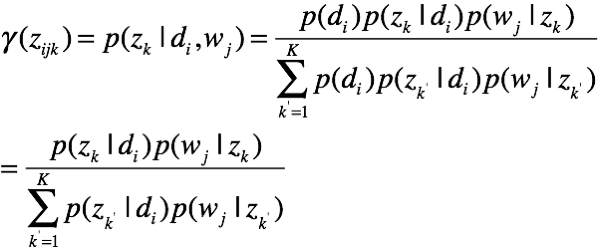 有一对样本的期望函数
有一对样本的期望函数
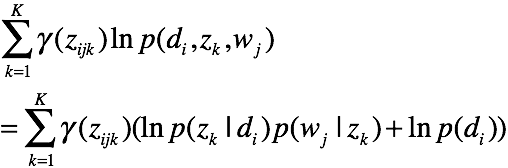
这里,我们取![]() 为常数。得到了整体的期望函数
为常数。得到了整体的期望函数
 这里,我们没有考虑词与词之间的相互顺序。接下来,我们要优化这个问题。
这里,我们没有考虑词与词之间的相互顺序。接下来,我们要优化这个问题。
(1) 对于![]() ,根据拉格朗日乘子法有代价函数:
,根据拉格朗日乘子法有代价函数:
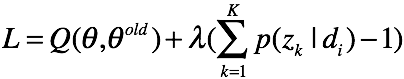 对
对 ![]() 求偏导,有
求偏导,有
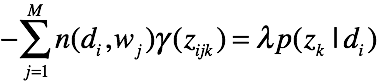
对K个主题方程求和,可得
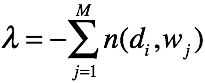
可得
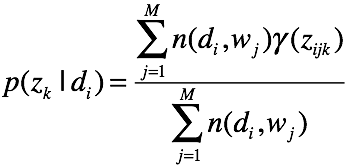
(2) 对于![]() ,根据拉格朗日乘子法有代价函数:
,根据拉格朗日乘子法有代价函数:
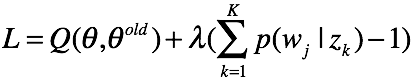
对![]() 求偏导,有
求偏导,有
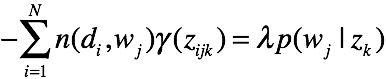
对M个词累加,可得
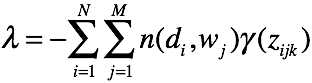
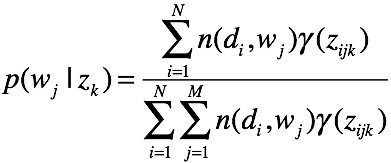 好的,我们可以总结一下过程了。
好的,我们可以总结一下过程了。
E step
计算后验概率
![]()
M step
迭代更新
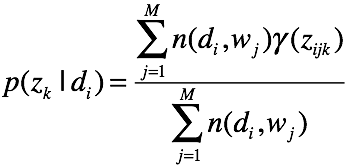
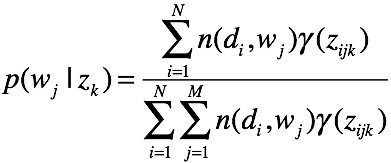
好了,我们推导了一遍混合高斯模型,又自行推导了一遍plsa.EM算法的精华基本掌握了。



