99+木头的博客&
♋Enjoy writing code.♑

[题解]ybt1365：FBI树(fbi)

ybt1365：FBI树(fbi)

 

[题目描述]

我们可以把由“0”和“1”组成的字符串分为三类：全“0”串称为B串，全“1”串称为I串，既含“0”又含“1”的串则称为F串。

FBI树是一种二叉树，它的结点类型也包括F结点，B结点和I结点三种。由一个长度为2N的“01”串S可以构造出一棵FBI树T，递归的构造方法如下：

T的根结点为R，其类型与串S的类型相同；

若串S的长度大于1，将串S从中间分开，分为等长的左右子串S1和S2；由左子串S1构造R的左子树T1，由右子串S2构造R的右子树T2。

现在给定一个长度为2N的“01”串，请用上述构造方法构造出一棵FBI树，并输出它的后序遍历序列。 

 

[输入格式]

第一行是一个整数N（0 ≤ N ≤ 10），第二行是一个长度为2N的“01”串。

 

[输出格式]

一行，这一行只包含一个字符串，即FBI树的后序遍历序列。

 

[输入样例]

3
10001011

 

[输出样例]

IBFBBBFIBFIIIFF

 

[解法1（常规建树）]

请看任天祥大佬代码：

  1 #include<cstdio>
  2 
  3 #include<iostream>
  4 
  5 #include<cstring>
  6 
  7 #include<cstdlib>
  8 
  9 using namespace std;
 10 
 11 int N;
 12 
 13 struct FBI
 14 
 15 {
 16 
 17     FBI *l,*r;
 18 
 19     char R;
 20 
 21 }*root;
 22 
 23 void build(string c,FBI **pr)      //新建节点的串与该节点位置
 24 
 25 {
 26 
 27       FBI *d;
 28 
 29     d=(FBI *)malloc(sizeof(FBI));              //位置申请空间
 30 
 31     
 32 
 33     if(c.length()==1)                   //边界
 34 
 35     {
 36 
 37         switch (c[0])          
 38 
 39         {
 40 
 41             case '0': d->R='B';//识别
 42 
 43             break;
 44 
 45             case '1': d->R='I';
 46 
 47             break;
 48 
 49         }
 50 
 51         *pr=d;
 52 
 53         d->l=NULL;         //这两句贼重要，要不然输出无边界。
 54 
 55         d->r=NULL;
 56 
 57         return;
 58 
 59     }
 60 
 61    
 62 
 63       int mid=c.length()/2;       //串分两半
 64 
 65     string s1,s2;                       //串分两半
 66 
 67     s1=c.substr(0,mid);
 68 
 69     s2=c.substr(mid,mid);              //指针指空
 70 
 71     FBI *dl,*dr;
 72 
 73     build(s1,&(d->l));                    //递归建树
 74 
 75     build(s2,&(d->r));  
 76 
 77       dl=d->l;
 78 
 79     dr=d->r;                 
 80 
 81     if((dl)->R=='B'&&(dr)->R=='B')
 82 
 83     {
 84 
 85         d->R='B';
 86 
 87         *pr=d;
 88 
 89         return;
 90 
 91     }
 92 
 93     if((dl)->R=='I'&&(dr)->R=='I')
 94 
 95     {
 96 
 97         d->R='I';
 98 
 99         *pr=d;
100 
101         return;
102 
103     }
104 
105     else d->R='F';
106 
107     *pr=d;
108 
109     return;
110 
111 }
112 
113  
114 
115 void backprin(FBI *a)
116 
117 {
118 
119     if(a)
120 
121     {
122 
123        backprin(a->l);
124 
125        backprin(a->r);
126 
127        printf("%c",a->R);
128 
129        return;
130 
131       }
132 
133    
134 
135 }
136 
137 int main ()
138 
139 {
140 
141       freopen("in.in","r",stdin);
142 
143       freopen("std.out","w",stdout);
144 
145     scanf("%d",&N);
146 
147     string x;
148 
149     cin>>x;
150 
151     build(x,&root);
152 
153     backprin(root);
154 
155     return 0;
156 
157 }

 

[解法2（递归骚代码）]

仔细观察我们就会发现对于一部分01串[l,r]对应节点i的fbi只与它左右两个子节点的fbi决定，而左右两个子节点对应的01串分别就是[l,(r+l)/2]和[(r+l)/2+1,r]由此我们可以得到递归式：

 

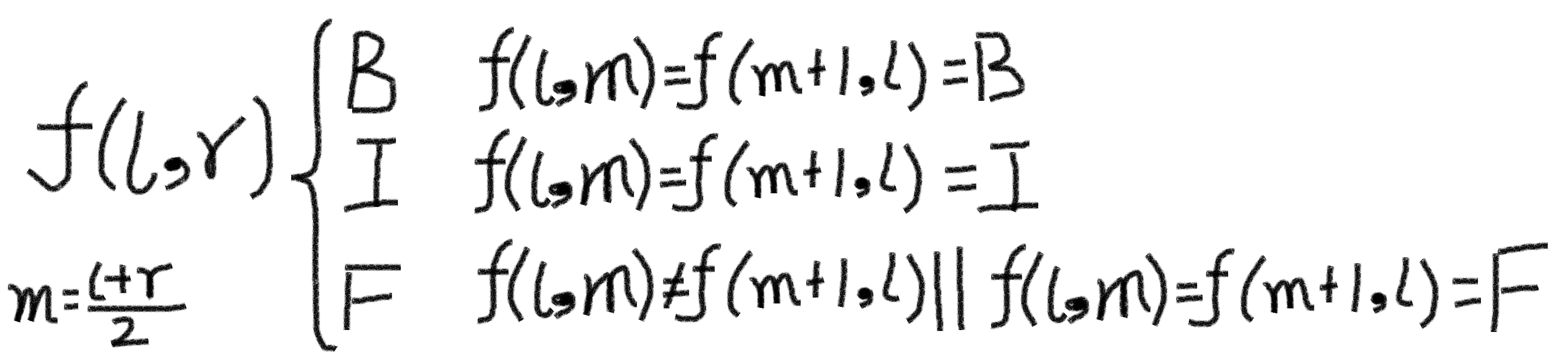
递归终点就是l=r直接返回这个01串对应值就好。如此我们得到了一下代码：

 

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cmath>
 4 #include<string>
 5 #include<cstring>
 6 #include<algorithm>
 7 using namespace std;
 8 bool fbi[1056];
 9 char dfs(int left,int right){
10     if(left==right){
11         if(fbi[left]){
12             printf("I");
13             return 'I';
14         }
15         else{
16             printf("B");
17             return 'B';
18         }
19     }
20     char l=dfs(left,left+(right-left)/2);
21     char r=dfs(left+(right-left)/2+1,right);
22     if(l=='F'||r=='F'){
23         printf("F");
24         return 'F';
25     }
26     if(l==r){
27         printf("%c",l);
28         return l;
29     }
30     else {
31         printf("F");
32         return 'F';
33     }
34 }
35 int main(){
36     int n;
37     scanf("%d",&n);
38     n=pow(2,n);
39     char temp;
40     for(int i=1;i<=n;++i){
41         scanf("\n%c",&temp);
42         fbi[i]=temp-'0';
43     }
44     dfs(1,n);
45     return 0;
46 }

2019-01-06 22:57:10

posted @ 2019-01-06 22:57  99+木头  阅读(1013)  评论(1)  编辑  收藏  举报