UVA10012 - How Big Is It?
| How Big Is It? |
Ian's going to California, and he has to pack his things, including his collection of circles. Given a set of circles, your program must find the smallest rectangular box in which they fit. All circles must touch the bottom of the box. The figure below shows an acceptable packing for a set of circles (although this may not be the optimal packing for these particular circles). Note that in an ideal packing, each circle should touch at least one other circle (but you probably figured that out).

Input
The first line of input contains a single positive decimal integer n, n<=50. This indicates the number of lines which follow. The subsequent n lines each contain a series of numbers separated by spaces. The first number on each of these lines is a positive integer m, m<=8, which indicates how many other numbers appear on that line. The next m numbers on the line are the radii of the circles which must be packed in a single box. These numbers need not be integers.
Output
For each data line of input, excluding the first line of input containing n, your program must output the size of the smallest rectangle which can pack the circles. Each case should be output on a separate line by itself, with three places after the decimal point. Do not output leading zeroes unless the number is less than 1, e.g. 0.543.
Sample Input
3
3 2.0 1.0 2.0
4 2.0 2.0 2.0 2.0
3 2.0 1.0 4.0
Sample Output
9.657
16.000
12.657
题目大意:给定N个圆,找出一个全排列,使得把所有圆包围所需要的矩形面积最小。
题解:看到N<=8,果断速度写了个dfs,提交上去果断WA。。。想N久都木有想到原因,然后去看了下其他的人题解。
由于我是把所有的圆之间都看成是相切的,其实是不一定的。例如下图这种情况,用我的方法做就直接跪了。
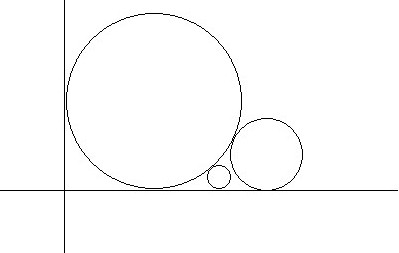
用我的方法显然算出来的答案比实际答案小。那该怎么做呢?具体做法就是把每个圆心的位置给求出来,第i个圆和前面所有圆相切时圆心距加上相切圆的圆心位置的最大值就是第i个圆的圆心位置。对于第一个圆和最后一个圆,他们可能并不与矩形的竖边相切,所以还要处理一下才行。
 View Code
View Code
1 #include<stdio.h> 2 #include<string.h> 3 #include<math.h> 4 #define MAXN 10 5 #define MAXS 0x7fffffff 6 int visit[MAXN]; 7 double r[MAXN],p[MAXN],rr[MAXN]; 8 int n; 9 double mins; 10 double max(double a,double b) 11 { 12 return a>b?a:b; 13 } 14 void dfs(int step) 15 { 16 int i,j; 17 double left,right; 18 if(step==n) 19 { 20 p[0]=rr[0]; 21 for(i=1; i<n; i++) 22 { 23 p[i]=p[i-1]+2*sqrt(rr[i]*rr[i-1]); 24 for(j=0; j<i-1; j++) 25 p[i]=max(p[i],p[j]+2*sqrt(rr[j]*rr[i])); 26 } 27 left=MAXS; 28 right=-MAXS; 29 for(i=0; i<n; i++) 30 { 31 if((p[i]-rr[i])<left) left=p[i]-rr[i]; 32 if((p[i]+rr[i])>right) right=p[i]+rr[i]; 33 } 34 if((right-left)<mins) mins=right-left; 35 return; 36 } 37 for(i=0; i<n; i++) 38 if(!visit[i]) 39 { 40 rr[step]=r[i]; 41 visit[i]=1; 42 dfs(step+1); 43 visit[i]=0; 44 } 45 } 46 int main(void) 47 { 48 int m,i; 49 scanf("%d",&m); 50 while(m--) 51 { 52 scanf("%d",&n); 53 mins=MAXS; 54 for(i=0; i<n; i++) 55 scanf("%lf",&r[i]); 56 memset(visit,0,sizeof(visit)); 57 dfs(0); 58 printf("%.3lf\n",mins); 59 } 60 return 0; 61 }




