●洛谷P2934 [USACO09JAN]安全出行Safe Travel

题链：

https://www.luogu.org/problemnew/show/P2934

题解：

 

最短路(树)，可并堆(左偏堆)，并查集。

个人感觉很好的一个题。
由于题目已经明确说明：从1点到每个点的最短路有且只有一条。
那么跑完最短路后，就可以得到一个最短路树，即每个点只有一个来源点。

然后来考虑，如果某一个u点无法从其最短路树上的father到达时，是个怎样的情况：

 

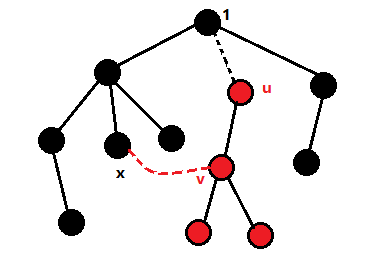
由于u无法从其父亲到达，所以如果还存在1到u的路径的话，

应该在其子树内(包括u)，存在一个v点，与子树外的某个节点x通过一条x和v之间的非树边，

形成这样一个从1到u的新最短路：1 → x →  v → u，

特别的，不能出现x是u的父亲且v就是u点的情况。(因为那条边已经被玩坏了2333)

那么这样的话，新的1到u的距离就是$dis[x]+e[x→v]+dis[v]-dis[u]$。

令$W(x,v)=dis[x]+e[x→v]+dis[v]$

因为要新的距离最小，所以就应该找到一对合法的(x,v)使得$W(x,v)$最小。

 

---

 

那么为什么答案就一定这种形式1 → x →  v → u的呢？

为何不能是1 → x → y → v → u，或者经过更多的子树外的节点呢？

 

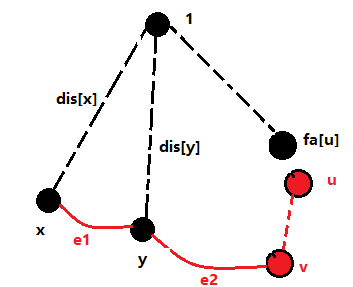
（图中的虚线表示最短路树上的路径）

如果经过了两个子树外的节点，那么距离d1就是：

$d1=dis[x]+e1+e2+dis[v]-dis[u]$

如果只经过了一个子树外的节点，比如是y，那么距离d2就是：

$d2=dis[y]+e2+dis[v]-dis[u]$

如果d2>d1的话，即按照之前的疑问，如果经过两个子树外节点会使得答案比经过一个子树外节点优，

那么：

$d2-d1>0$

$dis[y]+e2+dis[v]-dis[u]-(dis[x]+e1+e2+dis[v]-dis[u])>0$

$dis[y]-dis[x]-e1>0$

$dis[y]>dis[x]+e1$，与dis[y]是1到y的最短路矛盾，所以最优答案一定是只经过一个子树外节点。

(经过更多的子树外节点的情况可以自己试着证明一下。)

---

 

那么现在就需要对每个节点u，维护出对其合法的最小的W(x,v)，那么答案ANS[u]=W(x,v)-dis[u]。

而这个W(x,v)的维护就直接使用小根堆即可完成，

为了保证时间复杂度，我们需要从树下往上依次处理每个点的答案，

会涉及到把u节点的众多儿子v的堆合并，所以要用到可并堆(本人使用的是左偏堆)。

同时合并后，可能有些在堆里的W(x,v)就不合法了，因为有的x,v处在了同一个子树内，

但是不需要直接在堆里去删除，只用维护一个并查集，在取堆顶时判断该W(x,v)是否合法即可。

代码:

 

#include<bits/stdc++.h>
#define MAXN 100050
using namespace std;
int N,M;
int pre[MAXN],dis[MAXN],ANS[MAXN],order[MAXN];
struct Info{
	int x,y,w;
	bool operator < (const Info &rtm) const{
		return w<rtm.w;
	}
};
struct Edge{
	int ent;
	int to[MAXN*4],nxt[MAXN*4],val[MAXN*4],head[MAXN];
	Edge(){ent=2;}
	void Adde(int u,int v,int w){
		to[ent]=v; val[ent]=w; 
		nxt[ent]=head[u]; head[u]=ent++;
	}
}E;
struct UFSet{
	int fa[MAXN];
	void Reset(int n){
		for(int i=1;i<=n;i++) fa[i]=i;
	}
	int Findfa(int u){
		if(u==fa[u]) return u;
		else return fa[u]=Findfa(fa[u]);
	}
	void Union(int x,int y){
		static int fx,fy;
		fx=Findfa(x); fy=Findfa(y);
		if(fx==fy) return; fa[fx]=fy;
	}
	bool Insame(int x,int y){
		return Findfa(x)==Findfa(y);
	}
}S;
struct LT{
	//Define the LEN of the leaf is 1.
	int dnt;
	Info d[MAXN*4];
	int root[MAXN],ls[MAXN*4],rs[MAXN*4],len[MAXN*4];
	int Merge(int u,int v){
		if(!u||!v) return u+v;
		if(d[v]<d[u]) swap(u,v);
		rs[u]=Merge(rs[u],v);
		if(len[ls[u]]<len[rs[u]]) swap(ls[u],rs[u]);
		len[u]=len[rs[u]]+1;
		return u;
	}
	void Insert(int u,Info now){//Insert a new node into the heap of u
		++dnt; d[dnt]=now,len[dnt]=1;//As a new node, it's a leaf. 
		root[u]=Merge(root[u],dnt);
	}
	int Pop(int u){
		return Merge(ls[u],rs[u]);
	}
	Info Top(int u){
		static Info ret;
		while(ret=d[root[u]],ret.x&&S.Insame(ret.x,ret.y)){
		//	cout<<"Delete : "<<ret.x<<" < - > "<<ret.y<<" : "<<ret.w<<endl;
			root[u]=Pop(root[u]);
		}
		return ret;
	}
}H;
void Dijkstra(){
	typedef pair<int,int>Pii; int ont=0;
	priority_queue<Pii,vector<Pii>,greater<Pii> >Q;
	memset(dis,0x3f,sizeof(dis)); 
	Q.push(make_pair(dis[1]=0,1));
	while(!Q.empty()){
		Pii now=Q.top(); Q.pop();
		int u=now.second;
		if(now.first>dis[u]) continue;
		order[++ont]=u;
		for(int e=E.head[u];e;e=E.nxt[e]){
			int v=E.to[e];
			if(dis[v]<=dis[u]+E.val[e]) continue;
			dis[v]=dis[u]+E.val[e]; pre[v]=u;
			Q.push(make_pair(dis[v],v));
		}
	}
}
int main(){
	scanf("%d%d",&N,&M);
	for(int i=1,a,b,c;i<=M;i++)
		scanf("%d%d%d",&a,&b,&c),
		E.Adde(a,b,c),E.Adde(b,a,c);
	Dijkstra(); S.Reset(N);
	for(int i=N;i>=1;i--){
		int u=order[i];
		for(int e=E.head[u];e;e=E.nxt[e]){
			int v=E.to[e];
			if(v==pre[u]||S.Insame(u,v)) continue;
			H.Insert(u,(Info){u,v,dis[u]+dis[v]+E.val[e]});
		}
		Info now=H.Top(u);
		if(!now.x) ANS[u]=-1;
		else ANS[u]=now.w-dis[u];
		H.root[pre[u]]=H.Merge(H.root[pre[u]],H.root[u]);
		S.Union(pre[u],u);
	}
	for(int i=2;i<=N;i++) printf("%d\n",ANS[i]);
	return 0;
}