●BZOJ 1492 [NOI2007]货币兑换Cash

题链：

http://www.lydsy.com/JudgeOnline/problem.php?id=1492

题解：

斜率优化DP，CDQ分治

定义$DP[i]$为第i天结束后的最大收益。

由于题目给了良心的提示，转移就比较明显了：

令 $X_j，Y_j$ 分别表示用第j天的最大收益去全部买票，得到的A，B票的数量，

那么转移如下：

$DP[i]=min(X_jA_i+Y_jB_i)\quad(j<i)$ 第j天买的票在第i天全部卖出

$DP[i]=min(DP[i],DP[i-1])$ 不做任何交易，直接继承上一天的答案。

显然这个转移是 $O(N^2)$ 的。

（另外，$X_j=\frac{DP[j]R_j}{A_jR_j+B_j}，Y_j=\frac{DP[j]}{A_jR_j+B_j}$）

然后考虑优化，比如从j位置转移到i位置：

$DP[i]=X_jA_i+Y_jB_i$，可以化为以下形式：

$\mathbf{Y_j=-\frac{A_i}{B_i}X_j+\frac{DP[i]}{B_i}}$

现在在来看看这个式子，由于$A_i，B_i$都是确定的正数，可以考虑为常量，

如果把转移来源点$(X_j,Y_j)$都看成第一象限的点，

那么此时问题变为：

已知的斜率 $k=-\frac{A_i}{B_i}$，找到平面中的一个点，使得过该点的斜率为$k$的直线的纵截距最大。

 

---

怎样维护比较快捷呢？

做法是对这些点维护一个上凸壳，那么对于任何斜率$k$，使得纵截距最大的点一定在这个凸壳的顶点上。

即凸壳内部的点永远不可能贡献答案。

证明如下：

 

以上是第一种情况，下面再来看看内部的点与顶点的x不相同的情况。

先来看一个结论：

 

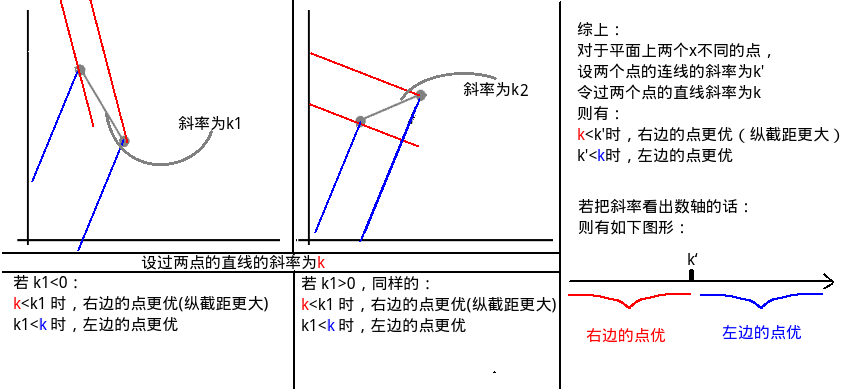
那么现在在来看看凸壳：

 

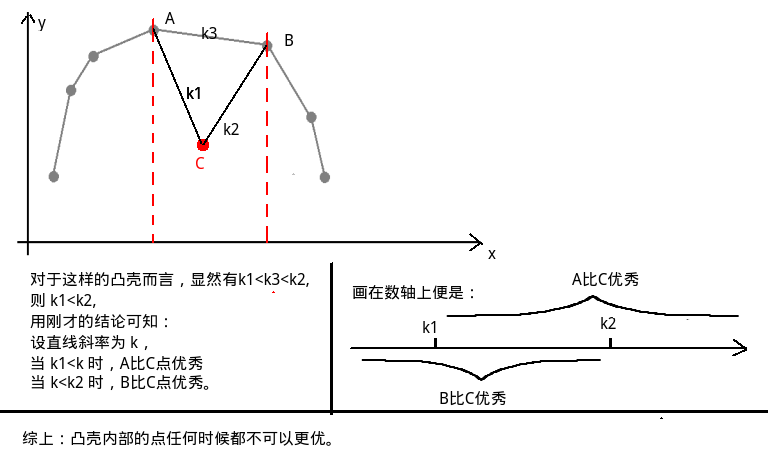
所以以上证明了使得纵截距最大的点一定在凸壳上。

---

到目前为止，我们的做法就是：

对于当前计算的DP[i]，把i的来源点j看成平面上的点，然后对这些点维护好一个上凸壳。

然后在凸壳上找到一个点使得过该点，且斜率为$k=-\frac{A_i}{B_i}$时的直线的纵截距最大。

关键点：

1.要注意DP转移的顺序，即只能从前面转移到后面。

2.维护好转移来源点的上凸壳。

由于Xi不随着i单增，所以不能一边从左枚举到右，一边O(1)插入一个新点并维护好凸壳。

同时询问不单调，所以不能直接像某些斜率优化的题一样用一个单调队列维护。

方法有两种：

1.CDQ分治：$O(Nlog_2N)$

分治的每一层，对于l~mid的点维护好一个凸壳，

然后mid+1~r点按$-\frac{A_i}{B_i}$从大到小排好序，然后扫一遍凸壳给mid+1～r的点贡献答案。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 100500
using namespace std;
const double eps=1e-10;
double A[MAXN],B[MAXN],R[MAXN];
double X[MAXN],Y[MAXN],DP[MAXN];
int h[MAXN],N;
int sign(double x){
	if(-eps<=x&&x<=eps) return 0;
	return x>eps?1:-1;
}
bool cmp(int i,int j){
	return sign(-A[i]/B[i]-(-A[j]/B[j]))>0;
}
bool cmp2(int i,int j){
	return sign(X[i]-X[j])<0;
}
struct Moque{//斜率单调递减的上凸壳
	int q[MAXN],l,r;
	void Reset(){l=1;r=0;}
	#define Slope(i,j) ((Y[i]-Y[j])/(X[i]-X[j]))
	void Push(int i){
		if(l<=r&&sign(X[i]-X[q[r]])==0)
			{if(sign(Y[i]-Y[q[r]])>0) r--;else return;}
		while(l+1<=r&&sign(Slope(i,q[r])-Slope(q[r],q[r-1]))>=0) r--;
		q[++r]=i;
	}
	int Query(int i){
		while(l+1<=r&&sign(Slope(q[l],q[l+1])-(-A[i]/B[i]))>0) l++;
		return q[l];
	}
}Q;
void solve(int l,int r){
	static double MAXDP=0;
	static int tmp[MAXN],cl,cr,p;
	if(l==r){
		Y[h[l]]=DP[h[l]]/(A[h[l]]*R[h[l]]+B[h[l]]);
		X[h[l]]=Y[h[l]]*R[h[l]];
		return;
	}
	int mid=(l+r)>>1; cl=l; cr=mid+1;
	for(int i=l;i<=r;i++)
		if(h[i]<=mid) tmp[cl++]=h[i];
		else tmp[cr++]=h[i];
	for(int i=l;i<=r;i++) h[i]=tmp[i];
	solve(l,mid); Q.Reset();
	for(int i=l;i<=mid;i++) Q.Push(h[i]),MAXDP=max(MAXDP,DP[h[i]]);
	for(int i=mid+1,j;i<=r;i++){
		j=Q.Query(h[i]);
		DP[h[i]]=max(DP[h[i]],MAXDP);
		DP[h[i]]=max(DP[h[i]],X[j]*A[h[i]]+Y[j]*B[h[i]]);
	}
	solve(mid+1,r); cl=l; cr=mid+1; p=l;
	while(cl<=mid||cr<=r){
		if(cl>mid) tmp[p]=h[cr],cr++;
		else if(cr>r||sign(X[h[cl]]-X[h[cr]])<0) tmp[p]=h[cl],cl++;
		else tmp[p]=h[cr],cr++; p++;
	}
	for(int i=l;i<=r;i++) h[i]=tmp[i];
}
int main(){
	scanf("%d%lf",&N,&DP[1]);
	for(int i=1;i<=N;i++)
		h[i]=i,scanf("%lf%lf%lf",&A[i],&B[i],&R[i]);
//	printf("happy\n");
	sort(h+2,h+N+1,cmp);
	solve(1,N);
//	for(int i=1;i<=N;i++)
	printf("%.3lf\n",DP[N]);
	return 0;
}

2.Splay：$O(Nlog_2N)$

动态维护好凸壳并直接log级别询问的最优转移点即可，Splay要支持单点插入，区间删除。

（感觉凸壳和Splay搭在一起好奇妙（恶心），本来以为有1mol需要特判的东西，结果由于凸壳的特殊，都不用特判了。。。）

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 100500
using namespace std;
const double eps=1e-10;
double A[MAXN],B[MAXN],R[MAXN];
double X[MAXN],Y[MAXN],DP[MAXN];
int N;
int sign(double x){
	if(-eps<=x&&x<=eps) return 0;
		return x>eps?1:-1;
}
struct SPT{
	#define Slope(i,j) ((Y[i]-Y[j])/(X[i]-X[j]))
	int ch[MAXN][2],fa[MAXN],pre[MAXN],suf[MAXN],d[MAXN],sz,rt,t1,t2;	
	void Rotate(int x,int &k){
		static int y,z,ll,rr;
		y=fa[x]; z=fa[y];
		ll=ch[y][0]!=x; rr=ll^1;
		if(!z) k=x; else ch[z][ch[z][0]!=y]=x;
		fa[ch[x][rr]]=y; fa[y]=x; fa[x]=z;
		ch[y][ll]=ch[x][rr]; ch[x][rr]=y;
	}
	void Splay(int x,int &k){
		static int y,z;
		while(x!=k){
			y=fa[x]; z=fa[y];
			if(y!=k) ((ch[y][0]!=x)^(ch[z][0]!=y))?
				Rotate(x,k):Rotate(y,k);
			Rotate(x,k);
		}
	}
	int Insert(int &x,int dad,int i,int l,int r){//l，r维护新插入点的前驱后继
		if(!x){
			x=++sz; fa[x]=dad; d[x]=i; 
			suf[l]=x; pre[x]=l; suf[x]=r; pre[r]=x;
			Splay(x,rt); return sz;
		}
		if(sign(X[i]-X[d[x]])==0){//发现横坐标相同的点
			if(sign(Y[i]-Y[d[x]])>0){//留下纵坐标大的
				d[x]=i; Splay(x,rt); return x;
			}
			else return 0;//舍去纵坐标小的
		}
		if(sign(X[i]-X[d[x]])<0) return Insert(ch[x][0],x,i,l,x);
		else return Insert(ch[x][1],x,i,x,r);
	}
	void Findpre(int x,int i){
		if(!x) return;
		if(pre[x]){
			if(sign(Slope(i,d[x])-Slope(d[x],d[pre[x]]))>0)
				t1=x,Findpre(ch[x][0],i);
			else Findpre(ch[x][1],i);
		}
	}
	void Findsuf(int x,int i){
		if(!x) return;		
		if(suf[x]){
			if(sign(Slope(d[suf[x]],d[x])-Slope(d[x],i))>0)
				t2=x,Findsuf(ch[x][1],i);
			else Findsuf(ch[x][0],i);
		}
	}
	int Split(int ll,int rr){
		Splay(ll,rt);
		Splay(rr,ch[rt][1]);
		return ch[rr][0];
	}
	void Delete(int ll,int rr){//删除开区间(ll,rr)
		static int p;
		p=Split(ll,rr);
		if(!p) return;
		ch[rr][0]=0; fa[p]=0;
		suf[ll]=rr; pre[rr]=ll;//维护好前驱后继
	}
	void Push(int i){
		static int p;
		p=Insert(rt,0,i,0,0);//插入后，被旋转到根
		if(!p) return;
		if(pre[p]&&suf[p]&&sign(Slope(d[suf[p]],d[p])-Slope(d[p],d[pre[p]]))>0){//判断是否在凸壳内，是的话就删除并退出
			Delete(pre[p],suf[p]);
			return;
		}
		t1=t2=0;//以下维护凸壳
		Findpre(ch[rt][0],i);
		Findsuf(ch[rt][1],i);
		if(t1) t1=pre[t1],Delete(t1,p);
		if(t2) t2=suf[t2],Delete(p,t2);
	}
	int Query(double w){
		static int x; x=rt;
		while(x){
			if(pre[x]&&sign(Slope(d[x],d[pre[x]])-w)<0) x=ch[x][0];
			else if(suf[x]&&sign(Slope(d[suf[x]],d[x])-w)>0) x=ch[x][1];
			else break;
		}
		return d[x];
	}
}DT;
int main(){
	freopen("cash.in","r",stdin);
	freopen("cash.out","w",stdout);
	scanf("%d%lf",&N,&DP[1]);
	for(int i=1;i<=N;i++)
		scanf("%lf%lf%lf",&A[i],&B[i],&R[i]);
	Y[1]=DP[1]/(A[1]*R[1]+B[1]); X[1]=Y[1]*R[1];
	DT.Push(1);
	for(int i=2,j;i<=N;i++){
		j=DT.Query(-A[i]/B[i]);
		DP[i]=max(DP[i-1],X[j]*A[i]+Y[j]*B[i]);
		Y[i]=DP[i]/(A[i]*R[i]+B[i]); X[i]=Y[i]*R[i];
		DT.Push(i);
	}
	//for(int i=1;i<=N;i++)
		printf("%.3lf\n",DP[N]);
	return 0;
}