●BZOJ 3551 [ONTAK2010]Peaks(在线)

题链：

http://www.lydsy.com/JudgeOnline/problem.php?id=3551

题解：

最小生成树 Kruskal，主席树，在线

这个做法挺巧妙的。。。
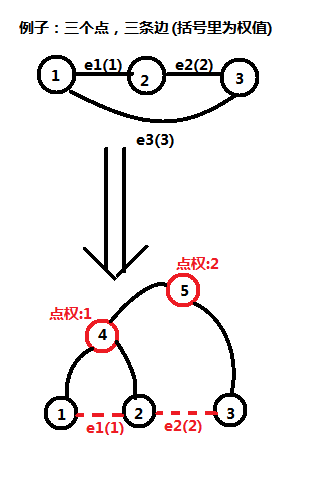
以Kruskal算法为基础，如果在用边 e(u,v,w) 合并 u 和 v 所在的联通块时，
我们新加一个节点 x(同时给它一个权值 w，即边 e 的权值)，
使得 u的联通块和 v的联通块通过这个节点 x 来合并为一个联通块。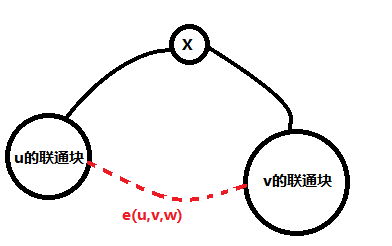

那么当Kruskal算法完成时，那么也就生成了一颗二叉树。

不难发现，这个二叉树非常棒啊：
1).叶子代表原图中的点，共有 N 个叶子
2).对于一个节点 x 来说，如果其点权为 w，
则表明 x 的子树的叶子节点所代表的的那些原图中的点可以通过边权不超过 w 的边互相通达。

所以按照如上方法生成了一颗二叉树后，
dfs一遍计算出每个节点所包含叶子节点的范围
(l[u],r[u]表示 u 这个节点的所包含叶子节点的范围是第 l[u]个叶子到第 R[u]个叶子)
然后按照叶子节点的顺序对原图的点的高度建立主席树。

每次查询v,x,k时，
就在二叉树中从该叶子向上倍增，
找到一个最大的子树使得该子树的根的权值不超过 x
然后得到范围 l[x] r[x]，并在主席树 rt[l[x]-1]~rt[r[x]] 中查询第 k 大就好了。

代码：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 105000 
using namespace std;
int H[MAXN],tmp[MAXN],Ord[MAXN];
int N,M,Q,tnt,Ont;
struct Edge{
	int u,v,w;
	bool operator <(const Edge &rtm)const{
		return w<rtm.w;
	}
}E[MAXN*5];
struct CMT{
	int rt[MAXN],ls[MAXN*20],rs[MAXN*20],cnt[MAXN*20],sz;
	void Insert(int &u,int l,int r,int p){
		sz++; cnt[sz]=cnt[u]; ls[sz]=ls[u]; rs[sz]=rs[u]; 
		u=sz; cnt[u]++;
		if(l==r) return;
		int mid=(l+r)>>1; 
		if(p<=mid) Insert(ls[u],l,mid,p);
		else Insert(rs[u],mid+1,r,p);
	}
	int Query(int v,int u,int l,int r,int K){
		if(l==r) return l;
		int mid=(l+r)>>1,rcnt=cnt[rs[u]]-cnt[rs[v]];
		if(K<=rcnt) return Query(rs[v],rs[u],mid+1,r,K);
		else return Query(ls[v],ls[u],l,mid,K-rcnt);
	}
	void Build(){
		for(int i=1;i<=N;i++){
			rt[i]=rt[i-1];
			Insert(rt[i],1,tnt,H[Ord[i]]);
		}
	}
}DT;//维护成重构的二叉树的底层叶子节点信息的主席树 
struct BT{
	int bel[MAXN*2],ls[MAXN*2],rs[MAXN*2],l[MAXN*2],r[MAXN*2],val[MAXN*2],fa[MAXN*2][20];
	int sz,rt;
	void Newnode(int u,int lson,int rson,int w){
		val[u]=w; bel[lson]=u; bel[rson]=u;
		ls[u]=lson; rs[u]=rson; 
	}
	int Find(int x){
		return x==bel[x]?x:bel[x]=Find(bel[x]);
	}
	void Dfs(int u,int f){
		fa[u][0]=f;
		for(int k=1;k<20;k++){
			if(!fa[u][k-1]||!fa[fa[u][k-1]][k-1]) break;
			fa[u][k]=fa[fa[u][k-1]][k-1];
		}
		if(!ls[u]&&!rs[u]){
			Ord[++Ont]=u; l[u]=r[u]=Ont;
			return; 
		} 
		Dfs(ls[u],u); Dfs(rs[u],u);
		l[u]=l[ls[u]]; r[u]=r[rs[u]];
	}
	void Build(){
		sz=N;
		for(int i=1;i<=2*N;i++) bel[i]=i;
		for(int i=1,fu,fv;i<=M;i++){
			fu=Find(E[i].u); 
			fv=Find(E[i].v);
			if(fu==fv) continue;
			Newnode(++sz,fu,fv,E[i].w);
		}
		rt=sz; Dfs(rt,0);
	}
	int Query(int u,int w,int K){
		for(int k=19;k>=0;k--){
			if(!fa[u][k]||val[fa[u][k]]>w) continue;
			u=fa[u][k];
		}
		int lrt=DT.rt[l[u]-1],rrt=DT.rt[r[u]];
		if(DT.cnt[rrt]-DT.cnt[lrt]<K) return -1;
		return tmp[DT.Query(lrt,rrt,1,tnt,K)];
	}
}GT;//根据Kruskal重构的二叉树 
void read(int &x){
	static int f; static char ch;
	x=0; f=1; ch=getchar();
	while(ch<'0'||'9'<ch){if(ch=='-') f=-1; ch=getchar();}
	while('0'<=ch&&ch<='9'){x=x*10+ch-'0'; ch=getchar();}
	x=x*f;
}
void readin(){
	read(N); read(M); read(Q);
	for(int i=1;i<=N;i++) read(H[i]),tmp[i]=H[i];
	sort(tmp+1,tmp+N+1); 
	tnt=unique(tmp+1,tmp+N+1)-tmp-1;
	for(int i=1;i<=N;i++) 
		H[i]=lower_bound(tmp+1,tmp+tnt+1,H[i])-tmp;
	for(int i=1;i<=M;i++)
		read(E[i].u),read(E[i].v),read(E[i].w);
	sort(E+1,E+M+1);
}
void answer(){
	static int V,X,K,lastANS;
	for(int i=1;i<=Q;i++){
		scanf("%d%d%d",&V,&X,&K);
		if(lastANS!=-1) V^=lastANS,X^=lastANS,K^=lastANS; 
		lastANS=GT.Query(V,X,K);
		printf("%d\n",lastANS);
	}
}
int main(){
	readin();
	GT.Build();
	DT.Build();
	answer();
	return 0;
}