●BZOJ 4559 [JLoi2016]成绩比较(容斥)
题链:
http://www.lydsy.com/JudgeOnline/problem.php?id=4559
题解:
容斥,拉格朗日插值法。
结合网上的另一种方法,以及插值法,可以把本题做到 O(N2)+O(N2+logN),
(本题的 O(N3)以及拉格朗日插值法在本题的用法,本篇目不再赘述。)
定义 f[k]表示至少碾压 k个人的方案数(只考虑分数相对大小关系,不考虑实际分数大小)。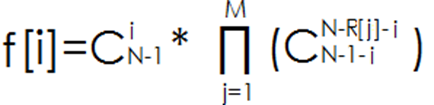
式子的含义是从N-1个人里面选K个人来碾压,然后对于每门科目,
再从没被碾压的人里选一些出来使得B神在本科目的排名为 R。
然后怎样由f[K]得到恰好有K个人被碾压的方案数ANS呢?
套路部分:
容斥系数如下:
f[K] :1
f[K+1] :-C(K+1,K)
f[K+2] :+C(K+2,K)
......
f[k+j] :(-1)^(j)*C(k+j,k)
这些东西加起来就得到 ANS了。
容斥系数怎么推出来的呢? 看看这个题目的解法,一样的套路,一样的味道。
求出了 ANS以后,
如果设 Y[i]表示第i门课程且B神排在第R[i]名时的分数分布方案。
则 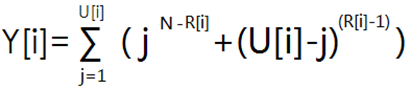
最后的答案就是 ANS*Y[1]*Y[2]*Y[3]*...*Y[M]
而这个 Y[i]可以用拉格朗日插值法求出。
代码:
#include<cstdio>
#include<cstring>
#include<iostream>
#define MAXN 105
#define _ %mod
#define filein(x) freopen(#x".in","r",stdin);
#define fileout(x) freopen(#x".out","w",stdout);
using namespace std;
const int mod=1000000007;
int dp[MAXN],U[MAXN],R[MAXN],C[MAXN][MAXN],Y[MAXN],inv[MAXN];
int N,M,K,ANS;
int pow(int a,int b){
int now=1;
while(b){
if(b&1) now=(1ll*now*a)_;
a=(1ll*a*a)_; b>>=1;
}
return now;
}
int Lagrange(int u,int r){
static int lpi[MAXN],rpi[MAXN],p[MAXN],ans,tmp;
lpi[0]=1; rpi[N+2]=1; ans=0;
for(int i=1;i<=N+1;i++){
p[i]=(1ll*p[i-1]+1ll*pow(i,N-r)*pow(u-i,r-1)_)_;
if(i==u) return p[i];
}
for(int i=1;i<=N+1;i++) lpi[i]=1ll*lpi[i-1]*(u-i)_;
for(int i=N+1;i>=1;i--) rpi[i]=1ll*rpi[i+1]*(u-i)_;
for(int i=1;tmp=1,i<=N+1;i++){
tmp=1ll*tmp*lpi[i-1]_*rpi[i+1]_*inv[i-1]_*inv[N+1-i]_*p[i]_;
tmp=(1ll*tmp*((N+1-i)&1?-1:1)+mod)_;
ans=(1ll*ans+tmp)_;
}
return ans;
}
int main()
{
scanf("%d%d%d",&N,&M,&K);
inv[0]=1; inv[1]=1;
for(int i=2;i<=N+1;i++) inv[i]=((-1ll*(mod/i)*inv[mod%i])_+mod)_;
for(int i=1;i<=N+1;i++) inv[i]=1ll*inv[i]*inv[i-1]_;
for(int i=1;i<=M;i++) scanf("%d",&U[i]);
for(int i=1;i<=M;i++) scanf("%d",&R[i]);
for(int i=0;i<=N;i++){
C[i][0]=1;
for(int j=1;j<=i;j++)
C[i][j]=(1ll*C[i-1][j-1]+C[i-1][j])_;
}
for(int i=1;i<=M;i++) Y[i]=Lagrange(U[i],R[i]);
for(int i=N-1;i>=K;i--)
{
dp[i]=C[N-1][i];
for(int j=1;j<=M;j++) dp[i]=1ll*dp[i]*C[N-i-1][N-R[j]-i]_;
ANS=(1ll*ANS+(((i^K)&1)?-1:1)*1ll*dp[i]*C[i][K]_+mod)_;
}
for(int i=1;i<=M;i++) ANS=1ll*ANS*Y[i]_;
printf("%d",(ANS+mod)_);
return 0;
}Do not go gentle into that good night.
Rage, rage against the dying of the light.
————Dylan Thomas


