17.10.27

上午

模拟考试，（是真的绝望，555。全部记录吧）
Prob.1（WA）太神了，没想出正解，也没打暴力、、、

题解：

代码：

#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
const int mod=998244353;
int ans,n,val=1;
int pow(int a,int b){
	int now=1;
	while(b){
		if(b&1) now=1ll*now*a%mod;
		a=1ll*a*a%mod; b>>=1;
	}
	return now;
}
int main(){
	freopen("A.in","r",stdin);
	freopen("A.out","w",stdout);
	scanf("%d",&n);
	for(int i=1,x;i<=n;i++){
		scanf("%d",&x);
		val=1ll*val*x%mod;
	}
	val=pow(val,mod-2);
	printf("%d",val);
	return 0;
}

他们没看出这个模型的，但是通过小数据化简出来了这个式子了，

我当时居然没有化简出来，好吧，是根本没化简,罪该万死、、、

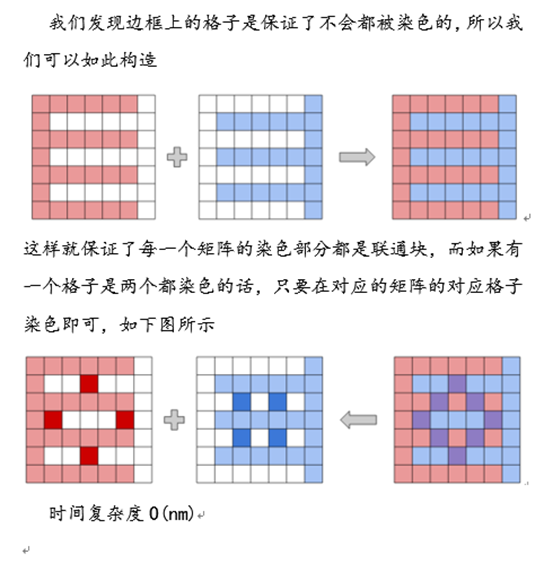
Prob.2（WA4组）构造题，但没构造出来、、、

题解、、、

代码：

#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
char mp1[505][505],mp2[505][505],x;
int n,m;
int main(){
	freopen("B.in","r",stdin);
	freopen("B.out","w",stdout);
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++){
			scanf(" %c",&x);
			if(x=='1') mp1[i][j]=mp2[i][j]='1';
			else mp1[i][j]=mp2[i][j]='0';
		}
	for(int i=1;i<=n;i+=2)
		for(int j=1;j<m;j++) mp1[i][j]='1';
	for(int i=1;i<=n;i++) mp1[i][1]='1';
	for(int i=2;i<=n;i+=2)
		for(int j=2;j<=m;j++) mp2[i][j]='1';
	for(int i=1;i<=n;i++) mp2[i][m]='1';
	for(int i=1;i<=n;i++){ 
		for(int j=1;j<=m;j++)
			printf("%c",mp1[i][j]);
		printf("\n");
	} 
	printf("\n");
	for(int i=1;i<=n;i++){ 
		for(int j=1;j<=m;j++)
			printf("%c",mp2[i][j]);
		printf("\n");
	}
	return 0;
}

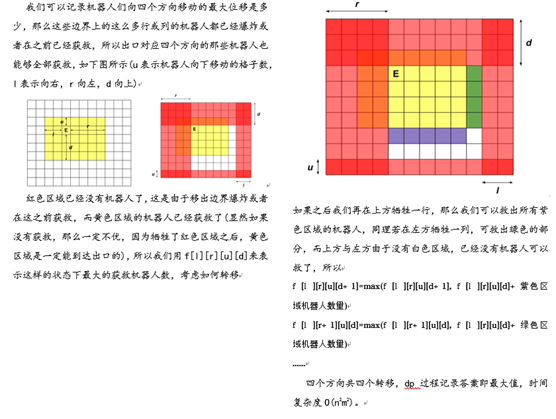
Prob.3（WA6组）神dp，根本没看出来是个dp？！

题解：（神dp，%%%）

代码：

#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
char mp[105][105];
short area[105][105],dp[105][105][105][105];
short sx,sy,n,m,ans;
short query(int x1,int y1,int x2,int y2){
	if(x1>x2||y1>y2) return 0;
	return area[x2][y2]+area[x1-1][y1-1]-area[x2][y1-1]-area[x1-1][y2];
}
int main(){
	freopen("C.in", "r", stdin);
	freopen("C.out", "w", stdout);
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		scanf("%s",mp[i]+1);
		for(int j=1;j<=m;j++){
			if(mp[i][j]=='E') sx=i,sy=j;
			area[i][j]=area[i-1][j]+area[i][j-1]-area[i-1][j-1]+(mp[i][j]=='o');
		}
	}
	short L=sy-1,R=m-sy,U=sx-1,D=n-sx;
	for(int l=0;l<=L;l++)
		for(int r=0;r<=R;r++)
			for(int u=0;u<=U;u++)
				for(int d=0;d<=D;d++){
					ans=max(ans,dp[l][r][u][d]);
					if(l+r<sy-1){
						int x=sx-u,y=sx+d;
						x=max(x,d+1); y=min(y,n-u);
						dp[l+1][r][u][d]=max(dp[l+1][r][u][d],(short)(dp[l][r][u][d]+query(x,sy-l-1,y,sy-l-1)));
					}
					if(l+r<m-sy){
						int x=sx-u,y=sx+d;
						x=max(x,d+1); y=min(y,n-u);
						dp[l][r+1][u][d]=max(dp[l][r+1][u][d],(short)(dp[l][r][u][d]+query(x,sy+r+1,y,sy+r+1)));
					}
					if(u+d<sx-1){
						int x=sy-l,y=sy+r;
						x=max(x,r+1); y=min(y,m-l);
						dp[l][r][u+1][d]=max(dp[l][r][u+1][d],(short)(dp[l][r][u][d]+query(sx-u-1,x,sx-u-1,y)));
					}
					if(u+d<n-sx){
						int x=sy-l,y=sy+r;
						x=max(x,r+1); y=min(y,m-l);
						dp[l][r][u][d+1]=max(dp[l][r][u][d+1],(short)(dp[l][r][u][d]+query(sx+d+1,x,sx+d+1,y)));
					}
				}
	cout<<ans;
	return 0;
}

下午

改错ing、、、
BOZJ 1077 [SCOI2008]天平

好题，差分约束 + 神判断。
定义两个数组：（a[i]表示i号砝码的重量）
dmax[i][j]:表示a[i]-a[j]最大为多少。（在判断时可以理解为使a[i]尽可能大，a[j]尽可能小）
dmin[i][j]:表示a[i]-a[j]最小为多少。（在判断时可以理解为使a[i]尽可能小，a[j]尽可能大）

按照读入数据，给两个数组赋上初值，然后两个floyd跑差分约束，得到正确的dmax数组和dmin数组

判断：（N^2枚举 C，D）
1). A + B > C + D:
    为保证结果唯一，
    我们想要使得等式左边(A + B)尽量小，等式右边(C + D)尽量大：
    表示为 A(小) + B(小) > C(大) + D(大)
    如果左边任然满足大于右边，则第一类答案 ans1++；

    把式子化简为差值的形式，便于使用dmax和dmin数组
     => 1)).A(小) - C(大) > D(大) - B(小)
            =>dmin[A][C] > dmax[D][B]
         2)).A(小) - D(大) > C(大) - B(小)
            =>dmin[A][D] > dmax[C][B]
    所以只要满足上面两个式子中的任意一个，就可以ans1++。
    if(dmin[A][C]>dmax[D][B]||dmin[A][D]>dmax[C][B]) ans1++;
        _____________________________________________________________________
     有一点需要注意：
         两个式子是可以相互化的，为什么需要判断两个？
         因为输入数据给出约束信息不一定完整，
         即我们可能计算出的信息满足第二个式子
         （即计算出 A与D的关系和 C与B的关系满足不等式），
         但是不一定满足第一个式子。
         （即不一定计算出了的 A与C的关系和 B与D的关系）
         所以只要任意一个式子满足就好了。
     另外，还有一点需要细想一下：
         那既然想上面所说的那样，约束信息不一定完整，
         那为什么不判一判 A + B > C + D这个式子还可以化出的另外两个差值不等式呢？
         比如 B(小) - C(大) > D(大) - A(小)这个式子。
         的确不用判，因为上式和 A(小) - D(大) > C(大) - B(小) [p]这个式子的信息是等价的。
         什么意思呢，B(小) - C(大) > D(大) - A(小)可以化为 dmin[B][C] - dmax[D][A]，
         即我们判断的任然是A与D之间的关系和 B与C之间的关系，和那个[p]式子判断的东西相同。

     之前说的“约束信息不一定完整”，就是因为我们可能知道
     AC、AD、BC、BD 这四组关系中的某两组关系，但不一定不知道另外两组的关系,
     所以要判断两个不等式，同时也只需要两个 “判断的信息不同的 ”不等式就好了。
        ______________________________________________________________________
剩下的就差不多了，自己化一化吧。
2).A + B = C + D
   if((dmin[A][C]==dmax[A][C]&&dmin[B][D]==dmax[B][D]&&dmin[A][C]+dmin[B][D]==0)||dmin[A][D]==dmax[A][D]&&dmin[B][C]==dmax[B][C]&&dmin[A][D]+dmin[B][C]==0)) ans2++;
3).C + D > A + B
   if(dmin[C][A]>dmax[B][D]||dmin[C][B]>dmax[A][D]) ans3++;

代码：

#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
int dmax[55][55],dmin[55][55]; 
int n,A,B,ans1,ans2,ans3;
int main(){
	char ch;
	scanf("%d%d%d",&n,&A,&B);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++){
			scanf(" %c",&ch);
			if(i==j||ch=='=') dmax[i][j]=dmin[i][j]=0;
			else if(ch=='+') dmax[i][j]=2,dmin[i][j]=1;
			else if(ch=='-') dmax[i][j]=-1,dmin[i][j]=-2;
			else dmax[i][j]=2,dmin[i][j]=-2;
		}
	for(int k=1;k<=n;k++)
		for(int i=1;i<=n;i++)
			for(int j=1;j<=n;j++)
				dmax[i][j]=min(dmax[i][j],dmax[i][k]+dmax[k][j]);
	for(int k=1;k<=n;k++)
		for(int i=1;i<=n;i++)
			for(int j=1;j<=n;j++)
				dmin[i][j]=max(dmin[i][j],dmin[i][k]+dmin[k][j]);
	for(int C=1;C<=n;C++)
		for(int D=1;D<C;D++){
			if(C==A||C==B||D==A||D==B) continue;
			if(dmin[A][C]>dmax[D][B]||dmin[A][D]>dmax[C][B]) ans1++;
			
			if((dmin[A][C]==dmax[A][C]&&dmin[B][D]==dmax[B][D]&&dmin[A][C]+dmin[B][D]==0)||
			(dmin[A][D]==dmax[A][D]&&dmin[B][C]==dmax[B][C]&&dmin[A][D]+dmin[B][C]==0)) ans2++;
			
			if(dmin[C][A]>dmax[B][D]||dmin[C][B]>dmax[A][D]) ans3++;
		}
	printf("%d %d %d",ans1,ans2,ans3);
	return 0;
}

晚上

BOZJ 1078 [SCOI2008]斜堆

考虑反着来依次撤掉最后一个。
看看最后一个插入的点满足什么性质：
   它是一直向左边插入的，且它没有右子树。[p]
但这种点不止一个。
我们考虑，对于一个满足该性质的点x，如果它的左子树（不是叶子）中还有一个点y也满足该性质，
那x和y到底哪个是最后一个插入的呢。答案是x。
如果是y的话，那按照斜堆的插入方法，y点经过x点时，会swap点x的左右子树，
即表明x在y插入之前，只有右儿子，没有左儿子（因为插入y后x只有左儿子，没有右儿子），
不符合斜堆的性质：任何非叶子节点都不可能单独存在右儿子。

所以对于那么多满足[p]的点，深度最小的点才是最后插入的。

另外如果y是x的左儿子，且y是叶子节点，x和y都可以作为最后插入的点。
为了让字典序最小（小顶堆），所以就让y是最后插入的。

代码：

#include<cstdio>
#include<cstring>
#include<iostream>
#define ls lson[u]
#define rs rson[u]
using namespace std;
int lson[105],rson[105],ans[105];
int n,rt;
void dfs(int u,int fa,int p){
	if((!ls&&!rs)||(!rs&&ls&&lson[ls])){
		lson[fa]=ls;
		ans[p]=u;
		return ;
	}
	dfs(ls,u,p);
	swap(ls,rs);
}
int main(){
	scanf("%d",&n);
	for(int i=2,x;i<=n+1;i++){
		scanf("%d",&x);
		if(x<100) lson[x+1]=i;
		else rson[x-100+1]=i;
	}
	lson[0]=1;
	for(int i=n+1;i>=1;i--) dfs(lson[0],0,i);
	for(int i=1;i<=n+1;i++) printf("%d ",ans[i]-1);
	return 0;
}

BOZJ 1079 [SCOI2008]着色方案

神dp，这个状态定义太强了。
因为每种颜料涂的次数不超过5次，就把这个写入状态，%%%
f[a][b][c][d][e][l]:
    还可以涂1次的有 a 个
    还可以涂2次的有 b 个
    、、、、、、、、、、
    还可以涂5次的有 e 个——的方案数。
（难在状态定义上，转移很简单）
（注意：要及时加 1ll*啊！！！！！int会乘爆的）

代码：

#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
const int mod=1000000007;
bool vis[16][16][16][16][16][6];
int f[16][16][16][16][16][6],t[6];
int n;
int dp(int a,int b,int c,int d,int e,int l){
	long long res=1ll*f[a][b][c][d][e][l];
	if(a+b+c+d+e==0) return 1;
	if(vis[a][b][c][d][e][l]) return res%mod;
	vis[a][b][c][d][e][l]=1;
	if(a) res+=1ll*(a-(l==2))*dp(a-1,b,c,d,e,1);
	if(b) res+=1ll*(b-(l==3))*dp(a+1,b-1,c,d,e,2);
	if(c) res+=1ll*(c-(l==4))*dp(a,b+1,c-1,d,e,3);
	if(d) res+=1ll*(d-(l==5))*dp(a,b,c+1,d-1,e,4);
	if(e) res+=1ll*(    e   )*dp(a,b,c,d+1,e-1,5);
	return f[a][b][c][d][e][l]=res%mod;
} 
int main(){
	scanf("%d",&n);
	for(int i=1,x;i<=n;i++)
		scanf("%d",&x),t[x]++;
	printf("%d",dp(t[1],t[2],t[3],t[4],t[5],0));
	return 0;
}

posted @ 2017-10-27 22:03 *ZJ 阅读(176) 评论(0) 编辑收藏举报

刷新页面返回顶部

*ZJ

有志者自有千计万计，无志者只感千难万难。

17.10.27

公告