面向对象第三单元作业总结

面向对象第三单元作业总结

JML语言和工具链

JML的基本语法

契约式设计或者Design by Contract (DbC)是一种设计计算机软件的方法。这种方法要求软件设计者为软件组件定义正式的，精确的并且可验证的接口，这样，为传统的抽象数据类型又增加了先验条件、后验条件和不变式。这种方法的名字里用到的“契约”或者说“契约”是一种比喻，因为它和商业契约的情况有点类似。

在契约式设计的背景下， JML(java model langauge)为契约式设计提供了支持。
jml的规格放在了注释里， // /* */ 来表示一些规则
\requires子句定义了方法的前置条件， 也就是程序运行前需要满足的条件
\ensures 子句定义了方法的后置条件， 也就是程序运行后需要满足的条件
\result 代表了方法执行的结果
\old(expr) 代表了表达式expr在方法执行前的值
\forall 对于给定范围的元素， 应满足条件
\exist 存在范围内的元素， 满足条件
\signal 用于抛出异常
\constraint用于限制对象转台的变化
\invariant 可见状态下都必须满足的特性

openjml的使用

通过openjml对程序规格进行动态和静态的检查
我采用了命令行的方式

java -jar ./openjml.jar -esc ~/Downloads/computer_science/schoolwork/OO/hw9/src/mycode/MyPath.java

smt solver验证

下载openjml以及使用

openjml是用来检查程序是否符合jml定义的规格的工具， 下载openjml.jar之后， 通过命令行运行， 主要有一下三种检查方式。
-check 仅仅对JML语法进行静态检查
-esc 规格静态检查， 看在代码没有运行的时候， 有没有不符合JML要求的操作。
-rac runtime check给定输入文件， 在代码运行的时候， 判断是否有不符合JML要求的操作。

进行检查

静态检查
在命令行中打入java -jar ./openjml.jar -esc -cp ~/Downloads/computer_science/schoolwork/OO/hw9/specs-homework-1-1.1-raw-jar-with-dependencies.jar ~/Downloads/computer_science/schoolwork/OO/hw9/src/mycode/MyPath.java

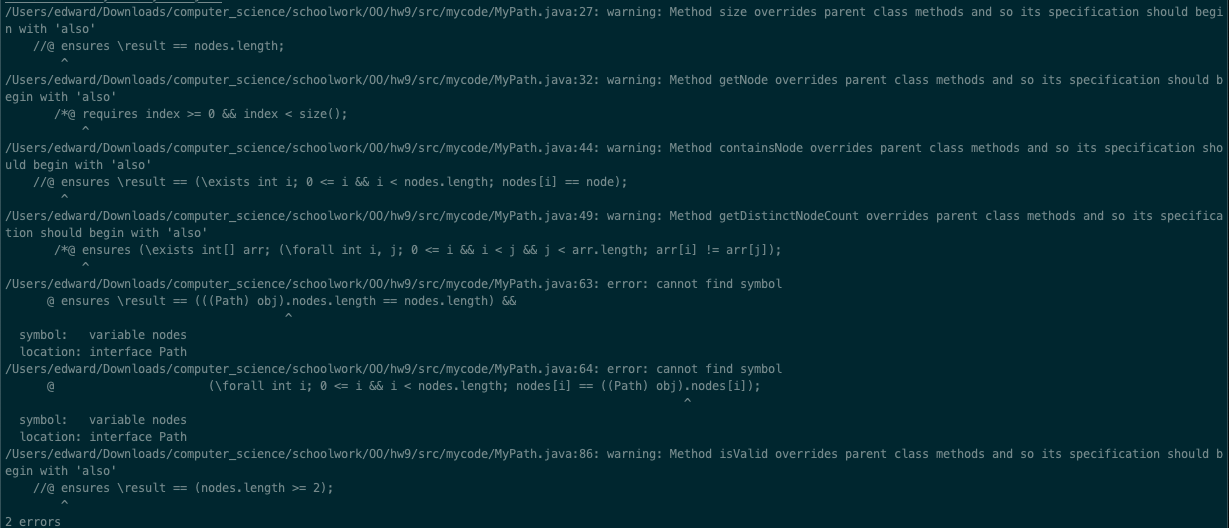
因为没有修改规格， 导致出现了两个错误和五个warning， 需要修改规格来让命名方式符合， 不过我觉得这样检测方法不是很科学， 每个人实现的方式不同， 在真实的软件开发中， 大家都很忙， 如果这么去调bug 的话很浪费时间， 单元测试会比这种方法更合适。

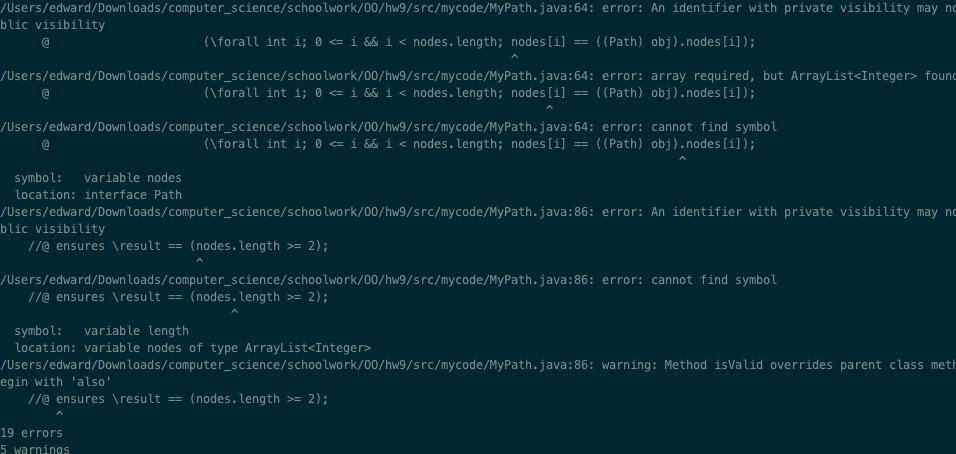
修改规格后出现了更多的报错
因为是通过容器和hashSet实现的代码， 和规格的描述不同。
目前掌握了SMT的用法， 但是由于代码的实现方式不同， 无法合理的用SMT进行测试， 有些为了满足JML语法而刻意去改的意味。 JML是很好的契约式设计的描述语言， 但是如果直接用SMT去进行测试的话， 还不够成熟。

jmlUnitNg

jmlUnitNg的用法

jmlUnitng是一款通过jml语言生成testNg测试数据的工具
首先从官网下载jml-uniting， 得到一个jar包
之后， 对于想要生成数据的java文件， 执行jml uniting
java -jar jmlunitng.jar [OPTIONS] path-list
其中options包括
-d 指定生成测试文件的目录
-cp , --classpath 给定一系列的class path
--public 只对public方法测试
比如

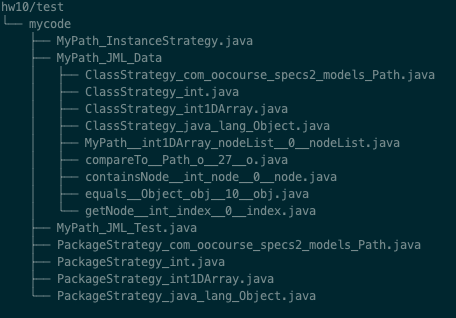
java -jar jmlunitng.jar -cp hw10/src/opensource/specs-homework-2-1.2-raw-jar-with-dependencies.jar hw10/src/mycode/MyPath.java

生成上图所示的目录
之后， 就可以使用testNg进行愉快的测试了

运行

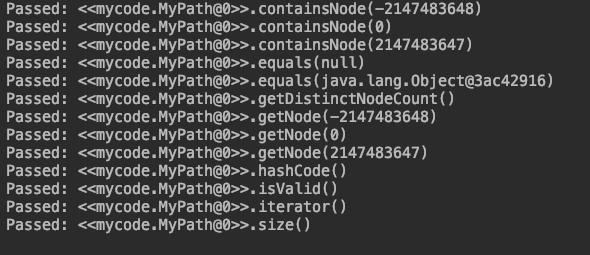
运行结果 通过了测试

架构梳理

第一次作业

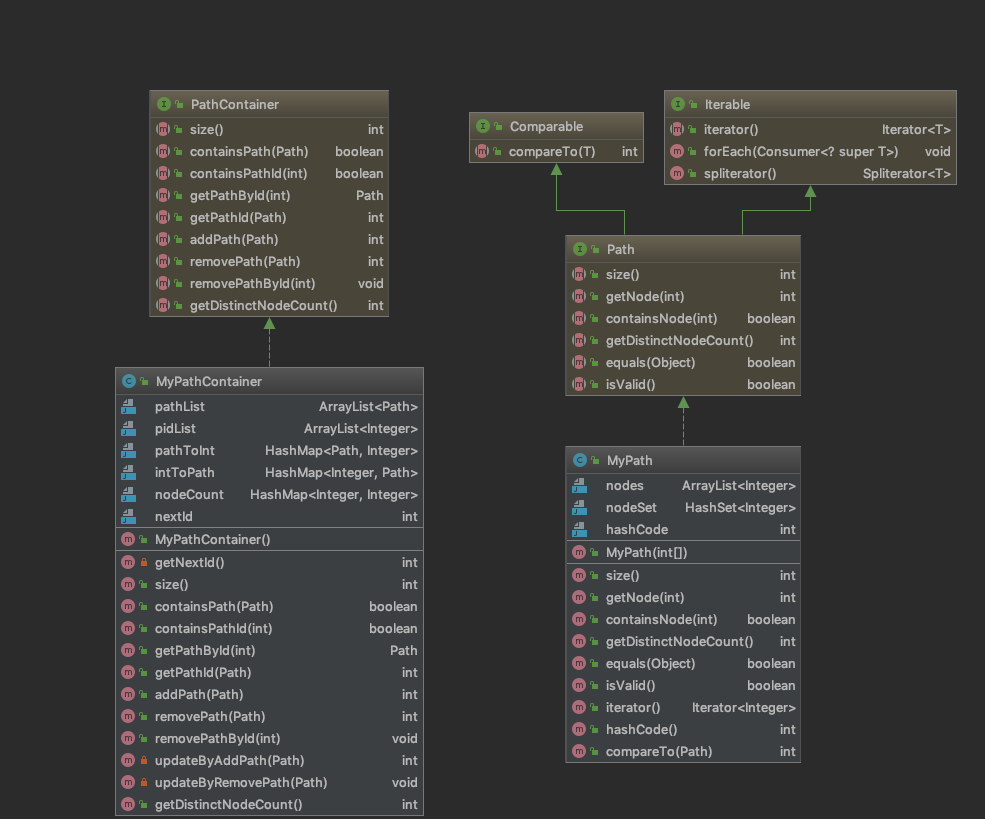
第一次作业整体难度不高， 需要修改MyPathContainer和MyPATH两个类。
架构上MyPathContainer实现了PathContainer接口， 作为路径的容器。
而Path是PathContainer的组成部分。

第二次作业

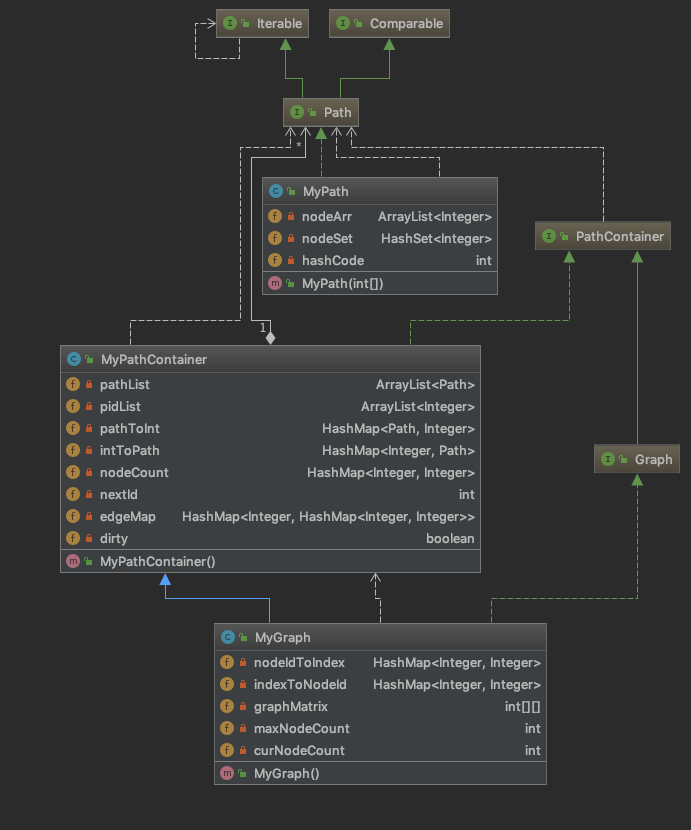
第二次作业利用PATHContainer， 实现了graph， 完成第一次作业的增量式设计。

第三次作业

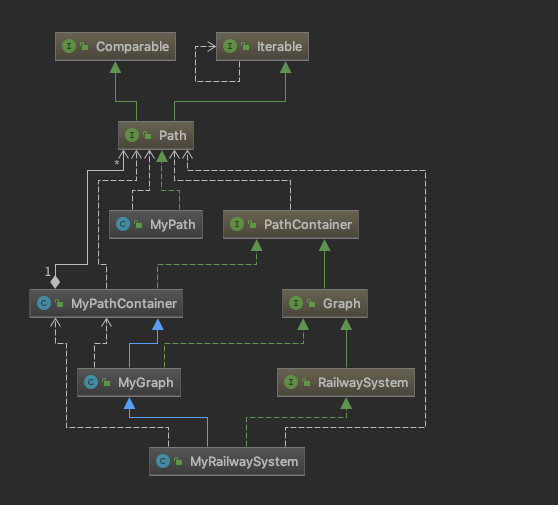
第三次作业在以前的基础上增加了railwaySystem类， 继承了Graph， 完成新的操作。

分析代码

第一次作业

第一次作业主要是增加和删除路径， 我用了三个HashMap来实现

    private HashMap<Path, Integer> pathToInt;
    private HashMap<Integer, Path> intToPath;
    private HashMap<Integer, Integer> nodeCount;

path到id, id到path， 以及一个node有多少个， 让每次查询的复杂度都接近O（1）
path hash值的计算方法如下

        for (int i = 0; i < nodeList.length; i++) {
            nodes.add(nodeList[i]);
            nodeSet.add(nodeList[i]);
            hashCode = hashCode * 31 + nodeList[i];
        }

最后再Container里通过update函数来加减PATH， 完成封装。

    private int updateByAddPath(Path path) {
        int curNextId = getNextId();
        pidList.add(curNextId);
        pathList.add(path);
        pathToInt.put(path, curNextId);
        intToPath.put(curNextId, path);
        for (int e : path) {
            if (nodeCount.containsKey(e)) {
                int oldValue = nodeCount.get(e);
                nodeCount.replace(e, oldValue + 1);
            } else {
                nodeCount.put(e, 1);
            }
        }
        return curNextId;
    }

第二次作业

第二次作业在第一次作业的基础上增加了graph
我用hash表和数组来存储图

    private HashMap<Integer, Integer> nodeIdToIndex;
    private HashMap<Integer, Integer> indexToNodeId;
    private int[][] graphMatrix;
    private int maxNodeCount;
    private int curNodeCount;

最后使用floyd算法来求最短路

    protected void buildMinDistance() {
        for (int mid = 0; mid < curNodeCount; mid++) {
            for (int i = 0; i < curNodeCount; i++) {
                for (int j = 0; j < curNodeCount; j++) {
                    if (checkNewRoad(i, mid, j)) {
                        updateCost(i, j, getNewCost(i, mid, j));
                    }
                }
            }
        }
    }

第三次作业

这次作业， 我采用的是拆点发， 然后dijstra
把三种最短路， 化为一个dijstra方法
type == 1, type2, type3 分别对应最低票价， 最少不满意度， 最少换成次数

    private void dijLeast(int from, int type) {
        for (int i = 0; i < distinctNodeCount; i++) {
            if (i == from) {
                dijMinDis[i] = 0;
                dijVisit[i] = true;
            } else {
                dijMinDis[i] = getGraphValue(from, i, type);
                dijVisit[i] = false;
            }
        }
        for (int i = 1; i < distinctNodeCount; i++) {
            int minCost = 10000000;
            int minPos = -1;
            int newCost;
            for (int j = 0; j < distinctNodeCount; j++) {
                if (!dijVisit[j] && dijMinDis[j] != -1) {
                    if (dijMinDis[j] < minCost) {
                        minCost = dijMinDis[j];
                        minPos = j;
                    }
                }
            }
            if (minPos == -1) {
                break;
            }
            dijVisit[minPos] = true;
            for (int j = 0; j < distinctNodeCount; j++) {
                if (!dijVisit[j] && getGraphValue(minPos, j, type) != -1) {
                    newCost = minCost + getGraphValue(minPos, j, type);
                    if (dijMinDis[j] == -1 || (dijMinDis[j] > newCost)) {
                        dijMinDis[j] = newCost;
                    }
                }
            }
        }
    }

心得体会

这三次作业， 让我体会到了对于一个工程是如何增量设计的。
传统瀑布式开发虽然好， 但是不够灵活， 从这三次作业， 我体会到了敏捷开发，一边设计， 一边写代码， 一边测试的过程， 加深的我对于开发的理解。
开发一个工程如同滚雪球， 开始只有基本的类和方法， 之后一次一次迭代， 继承， 封装， 最后达到要求。