5 分钟理解 Focal Loss 与 GHM——解决样本不平衡利器

Focal Loss for Dense Object Detection 是ICCV2017的Best student paper,文章思路很简单但非常具有开拓性意义，效果也非常令人称赞。

GHM(gradient harmonizing mechanism) 发表于 “Gradient Harmonized Single-stage Detector",AAAI2019，是基于Focal loss的改进，也是个人推荐的一篇深度学习必读文章。

第一部分 Focal Loss

Focal Loss的引入主要是为了解决难易样本数量不平衡（注意，有区别于正负样本数量不平衡）的问题，实际可以使用的范围非常广泛，为了方便解释，还是拿目标检测的应用场景来说明：

单阶段的目标检测器通常会产生高达100k的候选目标，只有极少数是正样本，正负样本数量非常不平衡。我们在计算分类的时候常用的损失——交叉熵的公式如下：

$CE=\left\{ \begin{aligned} -log(p) ,\quad if\quad y=1\\ -log(1-p),\quad if\quad y=0 \end{aligned} \right.$ (1)

为了解决正负样本不平衡的问题，我们通常会在交叉熵损失的前面加上一个参数 $\alpha$ ，即：

$CE=\left\{ \begin{aligned} -\alpha log(p) ,\quad if\quad y=1\\ -(1-\alpha)log(1-p),\quad if\quad y=0 \end{aligned} \right.$ (2)

但这并不能解决全部问题。根据正、负、难、易，样本一共可以分为以下四类：

file

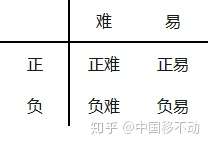
尽管 $\alpha$ 平衡了正负样本，但对难易样本的不平衡没有任何帮助。而实际上，目标检测中大量的候选目标都是像下图一样的易分样本。

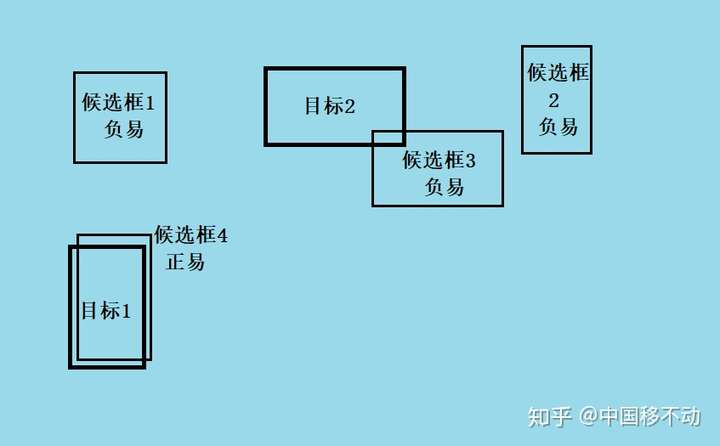
这些样本的损失很低，但是由于数量极不平衡，易分样本的数量相对来讲太多，最终主导了总的损失。而本文的作者认为，易分样本（即，置信度高的样本）对模型的提升效果非常小，模型应该主要关注与那些难分样本（这个假设是有问题的，是GHM的主要改进对象）

这时候，Focal Loss就上场了！

一个简单的思想：把高置信度(p)样本的损失再降低一些不就好了吗！

$FL=\left\{ \begin{aligned} -(1-p)^\gamma log(p) ,\quad if\quad y=1\\ \\ -p^\gamma log(1-p),\quad if\quad y=0 \end{aligned} \right.$ （3）

举个例， $\gamma$ 取2时，如果 $p=0.968$ , $(1-0.968)^2 \approx 0.001$ ，损失衰减了1000倍！

Focal Loss的最终形式结合了上面的公式（2）. 这很好理解，公式(3)解决了难易样本的不平衡，公式(2)解决了正负样本的不平衡，将公式（2）与（3）结合使用，同时解决正负难易2个问题！

最终的Focal Loss形式如下：

$FL=\left\{ \begin{aligned} -\alpha (1-p)^\gamma log(p) ,\quad if\quad y=1\\ -(1-\alpha) p^\gamma log(1-p),\quad if\quad y=0 \end{aligned} \right.$

实验表明 $\gamma$ 取2, $\alpha$ 取0.25的时候效果最佳。

file
这样以来，训练过程关注对象的排序为正难>负难>正易>负易。

这就是Focal Loss，简单明了但特别有用。

def py_sigmoid_focal_loss(pred,
                          target,
                          weight=None,
                          gamma=2.0,
                          alpha=0.25,
                          reduction='mean',
                          avg_factor=None):
    pred_sigmoid = pred.sigmoid()
    target = target.type_as(pred)
    pt = (1 - pred_sigmoid) * target + pred_sigmoid * (1 - target)
    focal_weight = (alpha * target + (1 - alpha) *
                    (1 - target)) * pt.pow(gamma)
    loss = F.binary_cross_entropy_with_logits(
        pred, target, reduction='none') * focal_weight
    loss = weight_reduce_loss(loss, weight, reduction, avg_factor)
    return loss

这个代码很容易理解，

先定义一个pt：

$\mathrm{p}_{t}=\left\{\begin{array}{c}{1-p, \text { tatget }=1} \\ {p, \text { target }=0}\end{array}\right.$

然后计算：

focal_weight = (alpha * target + (1 - alpha) *(1 - target)) * pt.pow(gamma)

也就是这个公式：

$FocalWeight=\left\{ \begin{aligned} \alpha (1-p)^\gamma ,\quad if\quad target=1\\ (1-\alpha) p^\gamma ,\quad if\quad target=0 \end{aligned} \right.$

再把BCE损失*focal_weight就行了

$FL=\left\{ \begin{aligned} -\alpha (1-p)^\gamma log(p) ,\quad if\quad target=1\\ -(1-\alpha) p^\gamma log(1-p),\quad if\quad target=0 \end{aligned} \right.$

代码来自于mmdetection\mmdet\models\losses，这个python版的sigmoid_focal_loss实现就是让你拿去学习的，真正使用的是cuda编程版。真是个人性化的好框架😂

第二部分 GHM

那么，Focal Loss存在什么问题呢？

首先，让模型过多关注那些特别难分的样本肯定是存在问题的，样本中有离群点（outliers），可能模型已经收敛了但是这些离群点还是会被判断错误，让模型去关注这样的样本，怎么可能是最好的呢？

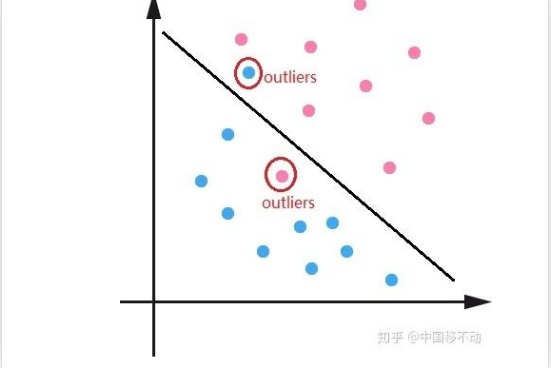
其次， $\alpha$ 与 $\gamma$ 的取值全凭实验得出，且 $\alpha$ 和 $\gamma$ 要联合起来一起实验才行（也就是说， $\alpha$ 和 $\gamma$ 的取值会相互影响）。

GHM(gradient harmonizing mechanism) 解决了上述两个问题。

Focal Loss是从置信度p的角度入手衰减loss，而GHM是一定范围置信度p的样本数量的角度衰减loss。

文章先定义了一个梯度模长g：

$g=|p-p^*|=\left\{ \begin{aligned} 1-p ,\quad if\quad p^*=1\\ p,\quad if\quad p^*=0 \end{aligned} \right.$

代码如下：

g = torch.abs(pred.sigmoid().detach() - target)

其中 $p$ 是模型预测的概率， $p^*$ 是 ground-truth的标签， $p^*$ 的取值为0或1.

g正比于检测的难易程度，g越大则检测难度越大。

至于为什么叫梯度模长，因为g是从交叉熵损失求梯度得来的：

$L_{CE}=\left\{ \begin{aligned} -log(p) ,\quad if\quad p^*=1\\ -log(1-p),\quad if\quad p^*=0 \end{aligned} \right.$

假定 $x$ 是样本的输出 $p = sigmoid(x)$ ,我们知道 $\frac{\partial p}{\partial x}=p(1-p)$ ，

那么 $\frac{\partial L_{C E}}{\partial x}=\frac{\partial L_{C E}}{\partial p}\frac{\partial p}{\partial x}$ ，可以求出

$\frac{\partial L_{CE}}{\partial x}=\left\{ \begin{aligned} p-1 ,\quad if\quad p^*=1\\ p ,\quad if\quad p^*=0 \end{aligned} \right.$ $=p-p^*$

$g=|\frac{\partial L_{CE}}{\partial x}|$

看下图梯度模长与样本数量的关系：

file

可以看到，梯度模长接近于0的样本数量最多，随着梯度模长的增长，样本数量迅速减少，但是在梯度模长接近于1时，样本数量也挺多。

GHM的想法是，我们确实不应该过多关注易分样本，但是特别难分的样本（outliers，离群点）也不该关注啊！

这些离群点的梯度模长d要比一般的样本大很多，如果模型被迫去关注这些样本，反而有可能降低模型的准确度！况且，这些样本的数量也很多！

那怎么同时衰减易分样本和特别难分的样本呢?太简单了，谁的数量多衰减谁呗！那怎么衰减数量多的呢？简单啊，定义一个变量，让这个变量能衡量出一定梯度范围内的样本数量——这不就是物理上密度的概念吗？

于是，作者定义了梯度密度 $GD(g)$ ——本文最重要的公式：

$GD(g)=\frac{1}{l_{\varepsilon}(g)}\sum_{k=1}^{N}{\delta_{\varepsilon}(g_{k},g)}$

$\delta_ {\varepsilon}(g_{k},g)$ 表明了样本1～N中，梯度模长分布在 $\left(g-\frac{\varepsilon}{2}, g+\frac{\varepsilon}{2}\right)$ 范围内的样本个数， $l_{\epsilon}(g)$ 代表了 $\left(g-\frac{\varepsilon}{2}, g+\frac{\varepsilon}{2}\right)$ 区间的长度。

因此梯度密度 $G D(g)$ 的物理含义是：单位梯度模长g部分的样本个数。

接下来就简单了，对于每个样本，把交叉熵CE×该样本梯度密度的倒数即可！

用于分类的GHM损失 $L_{G H M-C}=$ $=\sum_{i=1}^{N} \frac{L_{C E}\left(p_{i}, p_{i}^{*}\right)}{G D\left(g_{i}\right)}$ ， N是总的样本数量。

梯度密度的详细计算过程如下：

首先，把梯度模长范围划分成10个区域，这里要求输入必须经过sigmoid计算，这样梯度模长的范围就限制在0~1之间：

class GHMC(nn.Module):
    def __init__(self, bins=10, ......):
        self.bins = bins
        edges = torch.arange(bins + 1).float() / bins
......

>>> edges = tensor([0.0000, 0.1000, 0.2000, 0.3000, 0.4000, 
                  0.5000, 0.6000, 0.7000, 0.8000,0.9000, 1.0000])

edges是每个区域的边界，有了边界就很容易计算出梯度模长落入哪个区间内。

然后根据网络输出pred和ground true计算loss：

注意，不管是Focal Loss还是GHM其实都是对不同样本赋予不同的权重，所以该代码前面计算的都是样本权重，最后计算GHM Loss就是调用了Pytorch自带的binary_cross_entropy_with_logits，将样本权重填进去。

   # 计算梯度模长
        g = torch.abs(pred.sigmoid().detach() - target)
        # 目标检测中很多框被设置为忽略，因此需要额外考虑。
        # label_weight=1表示不忽略 label_weight=0表示忽略
        valid = label_weight > 0
        # 计算所有有效样本总数
        tot = max(valid.float().sum().item(), 1.0)
        # n 用来统计有效的区间数。
        # 假如某个区间没有落入任何梯度模长，密度为0，需要额外考虑，不然取个倒数就无穷了。
        n = 0  # n valid bins 
        # 通过循环计算落入10个bins的梯度模长数量
        for i in range(self.bins):
            inds = (g >= edges[i]) & (g < edges[i + 1]) & valid
            num_in_bin = inds.sum().item()
            if num_in_bin > 0:
                # 重点，所谓的梯度密度就是1/num_in_bin
                weights[inds] = tot / num_in_bin
                n += 1
        if n > 0:
            weights = weights / n
        # 把上面计算的weights填到binary_cross_entropy_with_logits里就行了
        loss = torch.nn.functional.binary_cross_entropy_with_logits(
            pred, target, weights, reduction='sum') / tot

看看抑制的效果吧，也就是文章开头的这张图片：

file

同样，对于回归损失：

$L_{G H M-R}==\sum_{i=1}^{N} \frac{A S L_{1}\left(d_{i}\right)}{G D\left(g r_{i}\right)}$ ,其中 $A S L_{1}$ 为修正的smooth L1 loss.

End~

因为本文着重论文的理解，很多细节没有写出，大家还是要去看一下原文的。

posted on 2020-03-19 13:53 Hebye 阅读(1816) 评论(1) 编辑收藏举报

刷新页面返回顶部