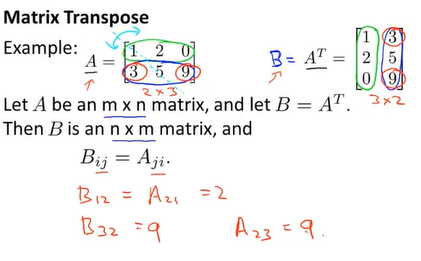吴恩达机器学习003矩阵和向量
吴恩达机器学习003矩阵和向量
标签: 机器学习 算法
##矩阵和向量
###矩阵
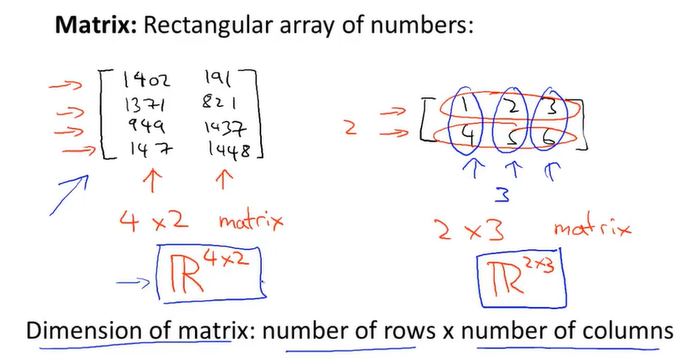
上图为矩阵的例子
表达矩阵的项,用下标来表示,第一个数是行,第二个数是列

###向量
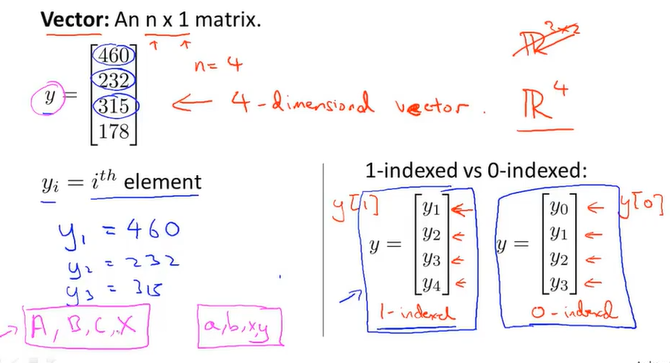
一般的,默认的是以1为下标开始,但有时也会用0作为下标开始,一般用大写字母表示矩阵,小写字母表示向量
##加法和标量乘法
###矩阵加法
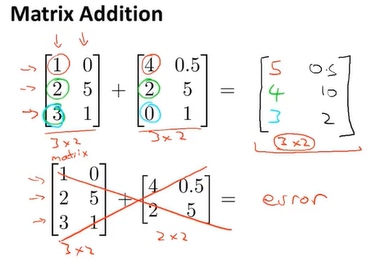
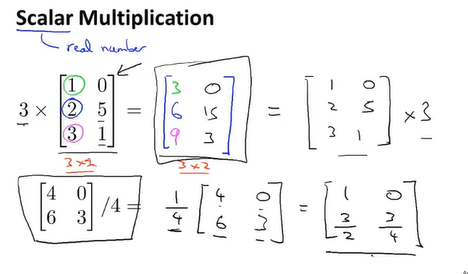
###标量乘法
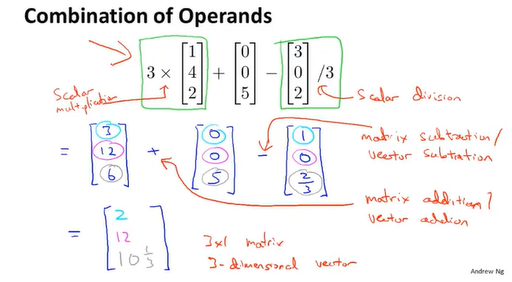
结果可以说是3*1的矩阵,也可以说是个三维列向量
###矩阵向量乘法
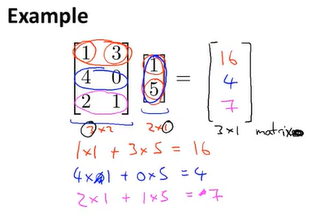
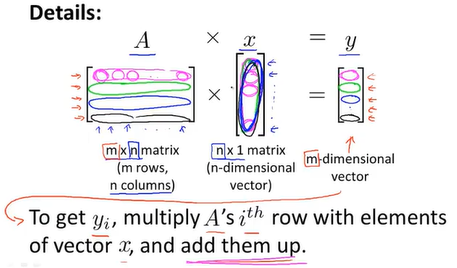
矩阵A乘一个列向量x时,列向量只能放在右边,同时矩阵的列数要和列向量的维度相等,乘得到的结果是一个列向量y,且y的行数和A相等。y从上往下的每一项对应着A的相应行和列向量x的内积。
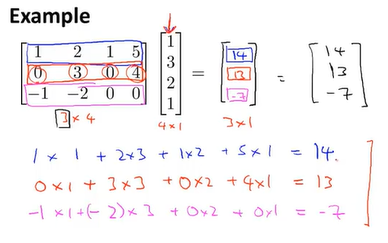
应用矩阵向量乘法于房价模型:可以一次测出一组参数多组预测值
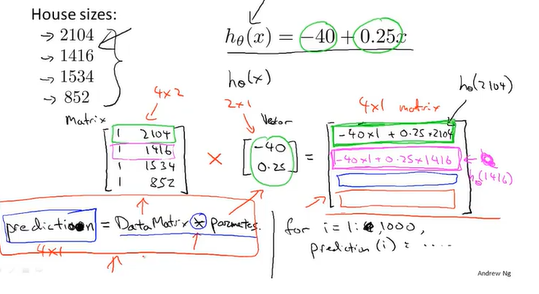
###矩阵乘法
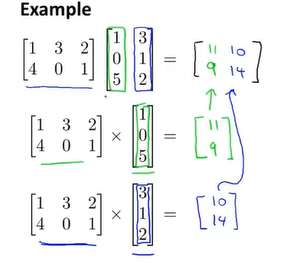

矩阵乘法可以简化为矩阵向量乘法,把B的每一列单独提出来和A相乘,得到了o个列向量,再把o个列向量组合起来得到矩阵乘法结果C。假如是m*n的矩阵乘n*o的矩阵的话,得到的结果是m*o矩阵,就是左边的矩阵行数是结果矩阵的行数,右边矩阵的列数是结果矩阵的列数,但首先左边的列数要和右边的行数相等矩阵才可以做乘法。

运用矩阵乘法于房价模型:可以一次性测试多组参数的多组预测值

##矩阵乘法特征
###矩阵乘法不符合交换律

###矩阵乘法符合结合律
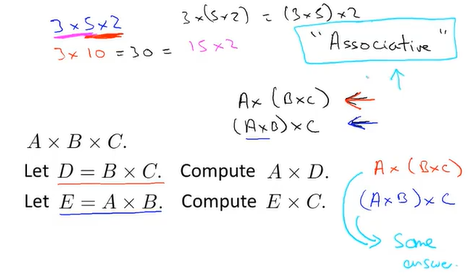
###单位矩阵
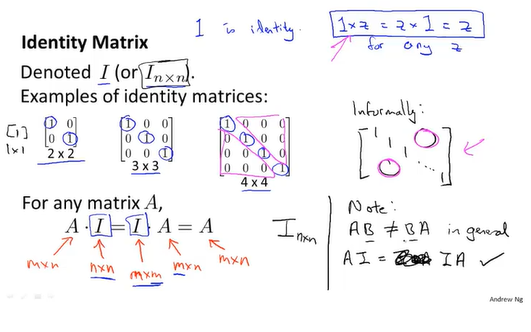
乘法交换律不适用于矩阵,但是当一个矩阵式单位矩阵时则成立,注意单位矩阵在m*n矩阵A左边时应该是m*m矩阵,在右边则是n*n矩阵
##逆和转置
###矩阵的逆

只有方阵才有逆,矩阵和自己的逆相乘得到单位矩阵,存在奇异矩阵或者退化矩阵没有逆
###矩阵的转置