算法设计与分析:分治算法
2-1 众数问题
问题描述
给定含有n个元素的多重集合S,每个元素在S中出现的次数称为该元素的重数。多重集S中重数最大的元素称为众数。例如,S={1,2,2,2,3,5}。多重集S的众数是2,其重数为3。
编程任务:对于给定的由n个自然数组成的多重集S,采用分治算法编程计算S的众数及其重数。
算法描述
- 对数组进行排序(例如利用快速排序,时间复杂度为\(O(NlogN)\))
- 求出中位数的统计信息
- 将数组进行划分,对子数组分别进行递归进行步骤2的求解
关键代码
class Solution {
int mode;/* 众数 */
int val;/* 重数 */
public void solve(int[] a, int l, int r) {
/* 左闭右闭区间 */
if (l > r) {
//区间为空
return;
}
int mid = l + (r - l) / 2;
int i = mid, j = mid;
//找到左侧第一个不等于a[mid]的位置
while (i >= 0 && a[i] == a[mid]) {
i--;
}
//找到右侧第一个不等于a[mid]的位置
while (a[j] == a[mid] && j <= a.length - 1) {
j++;
}
//j-i-1为中位数的重数
if (j - i - 1 > val) {
val = j - i - 1;
mode = a[mid];
}
//左侧可能找到结果
if (i - l + 1 > val) {
solve(a, l, i);
}
//右侧可能找到结果
if (r - j + 1 > val) {
solve(a, j, r);
}
}
}
结果分析

空间复杂度\(O(logN)\)
排序的时间复杂度\(O(NlogN)\),单个子问题的时间复杂度\(O(N)\),子问题的个数为\(O(logN)\)
总的时间复杂度为\(O(NlogN)\)
2-4 半数单集问题
问题描述
给定一个自然数n,由n开始可以依次产生半数集set(n)中的数如下:
(1) n ∈set(n);
(2) 在n的左边加上一个自然数,但该自然数不能超过最近添加的数的一半;
(3) 按此规则进行处理,直到不能再添加自然数为止。
注意,半数单集不是多重集,集合中已经有的元素不再添加到集合中。
算法描述
设\(f(n)\) = 半数集\(set(n)\)中元素的个数
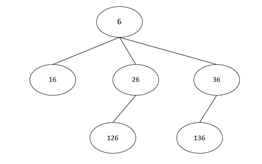
由图可知:\(f(6) = 1 + f(1) + f(2) + f(3)\)
归纳得出:
并且由此也可以发现,递归过程中存在大量的重叠子问题,可以用记忆化的方式进行优化。
同时题目要求的是半数单集(半数单集不是多重集,集合中已经有的元素不再添加到集合中)
在计算中,可能产生重复的元素是两位数
一个两位数\(x\)重复产生的条件是,在1位数\(y=x \% 10\)的半数集中已经产生了\(x\),因此有\(x/10<= y/2\)。
关键代码
class Solution {
int[] memo;
public Solution() {
/* 记忆化存储 */
memo = new int[1000];
}
public int halfSingleSet(int n) {
/* 如果f(n)之前算过,就不必再重复计算 */
if (memo[n] > 0) {
return memo[n];
}
int sum = 1;
for (int i = 1; i <= n / 2; i++) {
sum += halfSingleSet(i);
/* 重复计算的情况 */
if (i > 10 && i / 10 <= ((i % 10) / 2)) {
sum -= halfSingleSet(i / 10);
}
}
memo[n] = sum;
return sum;
}
}
结果分析

对于每个\(n\),\(f(n)\)仅会被计算一次,每次计算的时间复杂度是\(O(N)\)
所以总体的时间复杂度是\(O(N^2)\)
2-7 集合划分问题
问题描述
\(n\) 个元素的集合{1,2,…, \(n\) }可以划分为若干个非空子集。
例如,当 \(n\) = 4 时,集合{1,2, 3,4}可以划分为 15 个不同的非空子集如下:
{{1},{2},{3},{4}},
{{1,2},{3},{4}},
{{1,3},{2},{4}},
{{1,4},{2},{3}},
{{2,3},{1},{4}},
{{2,4},{1},{3}},
{{3,4},{1},{2}},
{{1,2},{3,4}},
{{1,3},{2,4}},
{{1,4},{2,3}},
{{1,2,3},{4}},
{{1,2,4},{3}},
{{1,3,4},{2}},
{{2,3,4},{1}},
给定正整数 n ,计算出 n 个元素的集合{1,2,…, n }可以划分为多少个不同的非空子集
算法描述
观察\(n\) = 4非空子集的划分,所有的划分中非空子集的个数为1,2,3, … , n
设\(f(n,m)\)表示n个元素的集合{1,2,…,\(n\)}可以划分为多少个不同的由m个非空子集组成的集合
针对于第\(n\)个元素,有两种选择:
- 将\(n\)归入第\(m\)个非空子集
- 将\(n\)单个元素直接作为第\(m\)个非空子集
即有递推关系式:
而总体的非空子集划分的个数结果为
关键代码
class Solution {
/* n个元素划分为由m个非空子集组成的集合的划分方法数 */
public int divSet(int n, int m) {
if (m == n || m == 1) {
return 1;
}
return m * divSet(n - 1, m) + divSet(n - 1, m - 1);
}
}
结果分析

递归树规模是指数增长的,子问题个数是\(O(2^N)\)的,而每个子问题都在\(O(1)\)时间内完成
所以总的时间复杂度为\(O(2^N)\)


