连接图算法CGR(二)
前言
第二篇论文研究了连接计划的优化问题。如前一篇博客所述,CGR路由中连接图的生成依赖于连接计划,连接计划指的是导航卫星系统中所有卫星的连接信息,由于在GNSS中,由于卫星平台的资源有限,每颗卫星能建立的星间链路是有限的(例如该篇论文在研究问题的时候令一颗卫星一次只能建立一条星间链路),如何确立这些星间链路的建立,形成一个优化的连接计划,以满足星间通信和星间测距的要求,是导航卫星形成的DTN网络中值得重视的问题。
连接计划
星间链路(ISL)
星间链路的建立能够实现星间测距和星间通信,星间测距使得GNSS能够实现自主导航,提高轨道和原子钟的准确度,减少对地面设施的依赖。星间通信可以将GNSS构建成一个全球性的网络。
受卫星星上资源的限制,每一颗卫星能够建立的星间链路是有限的。卫星与卫星之间的可见性也受卫星拓扑结构的影响。星间测距要求尽可能多的卫星之间建立尽可能多的星间链路,以获取更多的测距信息提高自主导航的准确性,而星间通信则需要考虑到卫星导航系统的时变性,两者实际上对连接计划的设计有着不同的导向。
如何生成一个最优化的连接计划,在星间测距和星间通信的需求之间达到一个均衡,是值得研究的问题。
拓扑应对
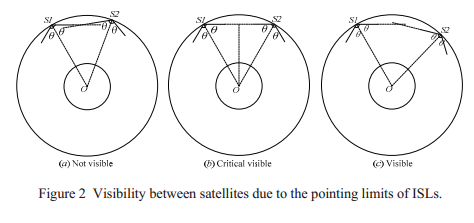
卫星可见性
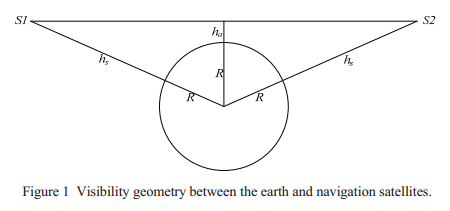
分两方面考虑,一是不被地球遮挡,二是卫星天线角度的限制,如图所示所以有:
2(R+hS)cosθ<d<2(R+hs)2−(R+ha)−−−−−−−−−−−−−−−−−√
基于FSA的拓扑应对
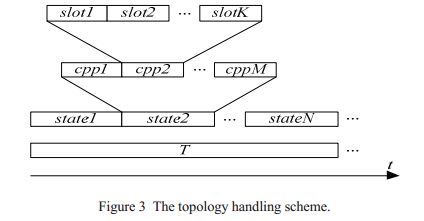
导航卫星周期T分为N个等长的时间间隔,每个时间间隔对应一个FSA状态,当且仅当两个卫星在这个FSA(Finite State Automation)状态一直保持可见状态时,才说这两个卫星在这个FSA状态可见,连接计划的设计基于每个FSA状态的固定可见性。
每个FSA状态分为M个等长的时间间隔,每个时间间隔称为一个连接计划周期cpp(contact plan period),每个cpp又分为K个等长时隙。
导航卫星在不同的时隙中在不同的可见卫星之间建立星间链路。连接计划的设计基于每一个FSA状态,在同一个FSA状态的cpp中,使用的是同一个连接计划。
连接计划设计问题的公式化
将连接计划的设计化为一个多限制条件下的最优解问题。优化目标为导航卫星网络的平均时延,这个平均是针对所有的卫星对和所有的时隙。最短传输路径由CGR路由计算得到。
对约束条件的理解:
(1) 两颗卫星要建立链路,那么它们一定是可见的。
(2)一颗卫星在一个时隙内只能建立一条星间链路
(3)(4)表示对称性约束
(5) 在所有时隙中,一个卫星队只能在一个时隙内建立一次星间链路,或者压根不建立链路。这一条能够确保一颗卫星在不同的时隙内和不同的卫星建立星间链路。来满足星间测距的最大数量。
基于模拟退火的连接计划设计
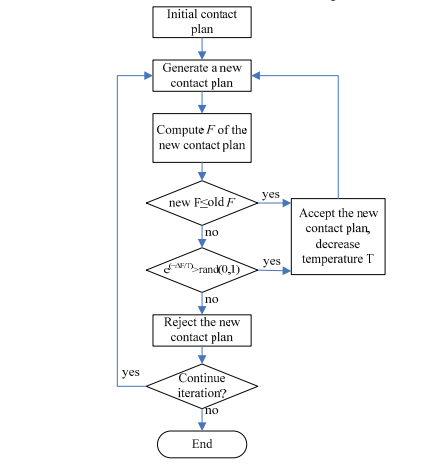
论文中采用了一种基于模拟退火的启发式算法来应对上述优化问题,来求得次优解。
大体思路:先随机生成一个连接计划,在此基础上生成一个新的连接计划,将两者进行计算和对比,若新连接计划的目标函数小于等于旧连接计划的目标函数,则采取新的连接计划,并降低温度系数T。按此思路不停的迭代,直到达到稳定状态为止。