考试杂写2
不知道为什么已经开始卡了，所以考虑再开一个写
编号和那个是连起来的
11.10/07 CSP-S模拟17 T3 三级跳
一道D (x)
一道数据结构 (x)
一道思维题 (√)
一眼想D，那就开D
定义\(f_i\)为终点为\(i\)的最大值，直接\(O(n^3)\)枚举转移点即可，式子显然
因为限定了区间，那么对于每个\(l\)要重新开始D一遍，所以效率极限是\(O(n^4)\)的
考虑优化D
枚举终点，再枚举转移点，我有没有枚举起点的必要？
没有，我们只需要找到一段区间的最大值即可
你想到了什么——线段树
于是我们就将D优化到了\(O(n^3logn)\)
继续优化，既然有了线段树了，那就深刻利用
我们依旧枚举重点，但是直接找这段的最大值，那么分讨这个值是作为起点还是中转点再找一个次大值即可
你猜对不对，不对
因为最大值的位置定了，那么就会限制区间，换句话说，你转移到终点不一定要过最大值，所以是fake的
那打正解吧
你考虑倒着维护一个单调栈，栈里维护的是中转点的可能点
一个数如果既靠左又够大，那么这个数作为中转点一定比更靠右还小的中转点更优秀，因为我可以覆盖住他们的贡献且贡献更大，而值更大的中转点的话不一定会不优，所以只需要维护一个单调栈即可
询问离线下来，倒着扫这个序列，每次弹栈进行区间更新，对每个询问进行区间查询最大值即可
时间复杂度\(O(nlogn)\)
结束
AC代码
#define abhwolxq bailan
#define WWW signed
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#define fre(x) freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define M 500005
#define ll long long
#define int long long
#define rep(i, a, b) for (int (i) = (a); (i) <= (b); (i)++)
#define dwn(i, a, b) for (int (i) = (a); (i) >= (b); (i)--)
using namespace std;
int wrt[20], TP;
inline int Max(int a, int b) { return a > b ? a : b; }
inline int read() {int x = 0;bool f = false;char c = getchar();while(!isdigit(c)) {if (c == '-') f = true;c = getchar();}do {x = (x << 1) + (x << 3) + (c ^ 48);}while(isdigit(c = getchar()));if (f) return -x;return x;}
inline void print(int x, bool op) {TP = 0;if (x < 0) putchar('-'), x = -x;while(x >= 10) wrt[++TP] = x % 10, x /= 10; putchar(x | 48);while(TP) putchar(wrt[TP--] | 48); if (op) putchar('\n'); else putchar(' ');}
int n, m, a[M], ans[M];
struct ASK {
int id, l, r;
friend bool operator< (const ASK &A, const ASK &B) { return A.l < B.l; }
}Q[M];
struct tree { int k, maxn, lz; }e[M << 2];
#define ls (rt << 1)
#define rs ((rt << 1) | 1)
inline void pushup(int rt) { e[rt].maxn = Max(e[ls].maxn, e[rs].maxn); }
inline void pushdown(int rt) {
if (e[rt].lz) {
e[ls].maxn = Max(e[ls].maxn, e[ls].k + e[rt].lz);
e[rs].maxn = Max(e[rs].maxn, e[rs].k + e[rt].lz);
e[ls].lz = Max(e[ls].lz, e[rt].lz);
e[rs].lz = Max(e[rs].lz, e[rt].lz);
e[rt].lz = 0;
}
}
void build(int rt, int l, int r) {
if (l == r) { e[rt].k = e[rt].maxn = a[l]; return; }
int mid = l + r >> 1;
build(ls, l, mid), build(rs, mid + 1, r);
e[rt].maxn = Max(e[ls].maxn, e[rs].maxn); e[rt].k = Max(e[ls].k, e[rs].k);
}
void updata(int rt, int l, int r, int L, int R, int val) {
if (L < 1 || L > R) return;
if (L <= l && r <= R) {
e[rt].maxn = Max(e[rt].maxn, e[rt].k + val);
e[rt].lz = Max(e[rt].lz, val);
return;
}
pushdown(rt); int mid = l + r >> 1;
if (L <= mid) updata(ls, l, mid, L, R, val);
if (R > mid) updata(rs, mid + 1, r, L, R, val);
pushup(rt);
}
int query(int rt, int l, int r, int L, int R) {
if (L <= l && r <= R) return e[rt].maxn;
pushdown(rt); int mid = l + r >> 1, maxn = 0;
if (L <= mid) maxn = query(ls, l, mid, L, R);
if (R > mid) maxn = Max(maxn, query(rs, mid + 1, r, L, R));
return maxn;
}
int stk[M], top;
WWW main() {
n = read();
rep(i, 1, n) a[i] = read();
build(1, 1, n);
m = read();
rep(i, 1, m) { Q[i].l = read(), Q[i].r = read(), Q[i].id = i; }
sort(Q + 1, Q + 1 + m);
int j = m;
dwn(i, n, 1) {
while(top && a[i] > a[stk[top]]) updata(1, 1, n, 2 * stk[top] - i, n, a[i] + a[stk[top]]), top--;
if (top) updata(1, 1, n, 2 * stk[top] - i, n, a[i] + a[stk[top]]);
stk[++top] = i;
while(Q[j].l == i) ans[Q[j].id] = query(1, 1, n, Q[j].l, Q[j].r), j--;
}
rep(i, 1, m) print(ans[i], 1);
return 0;
}
12.9/27 CSP-S模拟13 T2 Xorum
一个非常不错的构造题
先让我对\(\color{black}{K} \color{red}{aguya}\)进行一个拜的膜
假设这个奇数在二进制位下第二位是\(0\)
那么长这个样子
然后我们将其左移移到最高位的1和最低位的1在一个位置
得到了下面这个东西
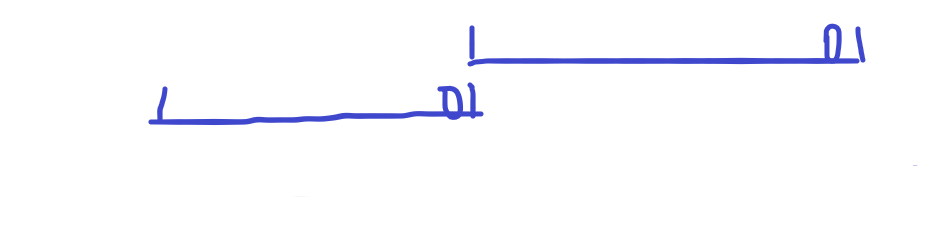
先加一下得到这个
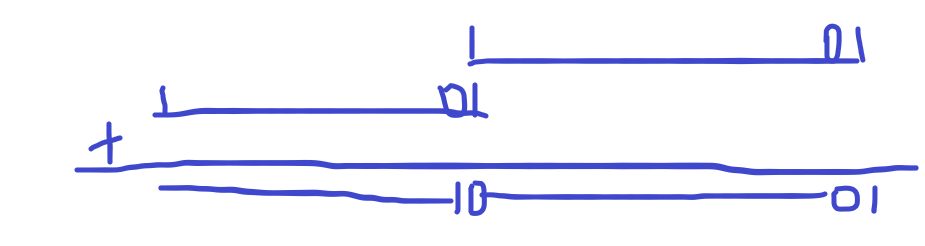
然后再异或一下得到这个
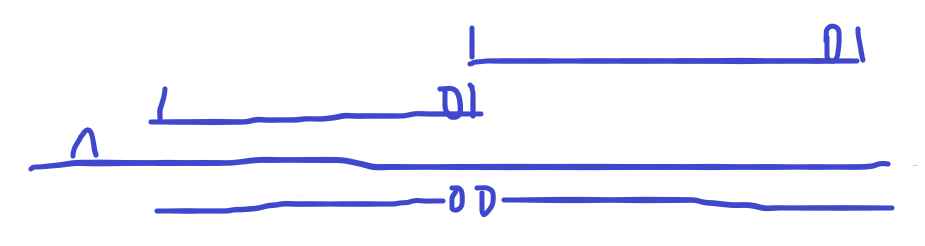
我们将这两个东西异或一下得到一个很好看的东西
其他的位置都是零
这是个什么东西捏，这是比最高位的1更高一位的1
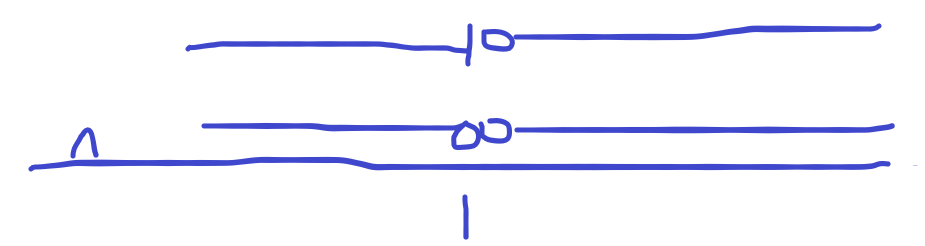
那么我们就将这个东西左移，通过异或的操作把一开始左移得到的那个东西所有高位的1给消掉
那么我就只剩下了原数最高位的1，然后我异或一下就消掉了
于是我们得到了消掉最高位1的办法
效率是\((log^2n)\)的
那么如果第二位不是0，也很好解决，你先把原数左移一位异或一下就好了
结束
AC代码
#define abhwolxq bailan
#define WWW signed
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#define M 100005
#define ll long long
#define int long long
#define fre(x) freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
using namespace std;
int wrt[20], TP;
inline int read() {int x = 0;bool f = false;char c = getchar();while(!isdigit(c)){if(c == '-') f = true;c = getchar();}do {x = (x << 1) + (x << 3) + (c ^ 48);}while(isdigit(c = getchar()));if (f) return -x;return x;}
inline void write(int x) {TP = 0; if (x < 0) putchar('-'), x = -x;while(x >= 10) wrt[++TP] = x % 10, x /= 10; wrt[++TP] = x;while(TP) putchar(wrt[TP--] | 48); putchar('\n');}
int cnt;
struct sb {
int op, k1, k2;
sb() {}
sb(int a, int b, int c) { op = a, k1 = b, k2 = c; }
}ans[M];
void keqing(int x, int cs) { while(cs--) ans[++cnt] = sb(1, x, x), x <<= 1; }
void chao(int x) {
for (int i = 20; i >= 1; i--) {//从高位向低位消去1
if (x & (1 << i)) {
keqing(x, i);
int y = x << i;
int z = x + y; ans[++cnt] = sb(1, x, y);
int f = x ^ y; ans[++cnt] = sb(2, x, y);
int g = z ^ f; ans[++cnt] = sb(2, z, f);
keqing(g, i - 1);
for (int j = i + 1; j <= (i << 1); j++) {
if (y & (1ll << j)) {
ans[++cnt] = sb(2, y, (1ll << j));
y ^= (1ll << j);
}
}
ans[++cnt] = sb(2, x, y);
x ^= y;
}
}
}
WWW main() {
int x = read();
if (x & (1 << 1)) {
ans[++cnt] = sb(1, x, x);
ans[++cnt] = sb(2, x, 2 * x);
x = (x ^ (x << 1));
}
chao(x);
printf("%lld\n", cnt);
for (int i = 1; i <= cnt; i++) printf("%lld %lld %lld\n", ans[i].op, ans[i].k1, ans[i].k2);
return 0;
}
13 10/10多校 T3 序列
一道斜率题
原式子是$$\sum_{l}^{r}{a_i} - k\sum_{l}^{r}{b_i}$$
每次询问给出\(p_j\)和\(k_j\)，要求\(p_j \in [l, r]\)
首先我们可以发现，\(l,r\)是相互独立的，意思就是左右端点的选取互不相干，所以原问题可以拆成两个问题独立处理
其次求和我们可以拆成前缀和，那么这个式子就剩下了四项
\[sa_r - sa_{l-1} - k \times sb_r + k \times sb_{l - 1}
\]
然后换换位置
\[k \times sb_{l - 1} - sa_{l-1} - k \times sb_r + sa_r
\]
所以最后的问题就来到了\(x \in [1,p_j],y \in[p_j+1,n]\)，求
\[max(k \times sb_x-sa_x) - min(k \times sb_y - sa_y)
\]
那么询问离线上李超线段树即可
结束（略微卡常）
AC代码
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize(fast)
#define abhwolxq bailan
#define WWW signed
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#define M 1000005
#define ll long long
#define int long long
#define inf 1000000000000000000
#define fre(x) freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define fin(x) freopen(#x ".in", "r", stdin)
#define rep(i, a, b) for (int (i) = (a); (i) <= (b); (i)++)
#define dwn(i, a, b) for (int (i) = (a); (i) >= (b); (i)--)
using namespace std;
int TP, wrt[20];
inline int Max(int a, int b) { return a > b ? a : b; } inline int Min(int a, int b) { return a < b ? a : b; }
inline int read() {int x = 0;bool f = false;char c = getchar();while(!isdigit(c)) {if (c == '-') f = true;c = getchar();}do {x = (x << 1) + (x << 3) + (c ^ 48);}while(isdigit(c = getchar()));if (f) return -x;return x;}
inline void print(int x, bool op) {TP = 0;if (x < 0) putchar('-'), x = -x;while(x >= 10) wrt[++TP] = x % 10, x /= 10; putchar(x | 48);while(TP) putchar(wrt[TP--] | 48); if (op) putchar('\n'); else putchar(' ');}
int n, m, lsh[M]; ll a[M], b[M], ans[M];
struct ASK {
int id, p, k;
friend bool operator< (const ASK &A, const ASK &B) { return A.p < B.p; }
}Q[M];
inline ll calc(int id, int x) { return b[id] * lsh[x] + a[id]; }
#define ls (rt << 1)
#define rs ((rt << 1) | 1)
int s[M << 2];
void change(int rt, int l, int r, int x) {
if (!s[rt]) { s[rt] = x; return; }
int mid = l + r >> 1, &y = s[rt];
if (calc(x, mid) > calc(y, mid)) swap(x, y);
if (calc(x, l) > calc(y, l)) change(ls, l, mid, x);
if (calc(x, r) > calc(y, r)) change(rs, mid + 1, r, x);
}
ll query(int rt, int l, int r, int pos) {
ll maxn = calc(s[rt], pos);
if (l == r) return maxn;
int mid = l + r >> 1;
if (pos <= mid) maxn = Max(maxn, query(ls, l, mid, pos));
else maxn = Max(maxn, query(rs, mid + 1, r, pos));
return maxn;
}
WWW main() {
n = read(), m = read();
rep(i, 1, n) a[i] = a[i - 1] + read(), b[i] = b[i - 1] + read();
rep(i, 1, m) {
Q[i].p = read(), Q[i].k = read(), Q[i].id = i;
lsh[i] = Q[i].k;
}
sort(Q + 1, Q + 1 + m);
sort(lsh + 1, lsh + 1 + m);
int cnt = unique(lsh + 1, lsh + 1 + m) - lsh - 1;
rep(i, 1, m) Q[i].k = lower_bound(lsh + 1, lsh + 1 + cnt, Q[i].k) - lsh;
int j = 1;
rep(i, 1, n) {
while(Q[j].p == i and j <= m) {
ans[Q[j].id] += query(1, 1, cnt, Q[j].k);
j++;
}
a[i] = -a[i];
change(1, 1, cnt, i);
}
j = m;
memset(s, 0, sizeof(s)); a[0] = -inf;
dwn(i, n, 1) {
a[i] = -a[i], b[i] = -b[i];
change(1, 1, cnt, i);
while(Q[j].p == i and j) {
ans[Q[j].id] += query(1, 1, cnt, Q[j].k);
j--;
}
if (!j) break;
}
rep(i, 1, m) print(ans[i], 1);
return 0;
}
14 9/22 CSP-S模拟9 T4 连续子段
不错的状压D
我们对连续段里已经选到的元素进行一个状的压
设\(f_{i,s}\)为选到了第\(i\)个位置状态为\(s\)的最少操作次数
那么到了第\(i\)个位置有两种情况，我选进去或者作为空位
考虑空位是什么，就是两边是我已经选好的连续段，而中间这个位置我是不要的，我要通过平移把这个玩意搞出去
那么这个空位的贡献就是\(min(l, r)\)，\(l,r\)就是左右两边连续段的大小
设\(len_s\)为状态\(s\)里\(1\)的个数，这个是可以预处理出来的
那么位置\(i\)作为空位的转移式子为
\[f_{i,j} = min(f_{i,j},f_{i-1,j}+min(len_j,len_{S \oplus j}))
\]
其中\(S\)是全集，意义就是我在前面依旧选好的和在后面选到还没选的去一个最小值来转移
再考虑我要选这个位置，则设新的u状态为\(t\)，转移式子为
\[f_{i,t} = min(f_{i,t},f_{i-1,j}+len_{j>>a_i})
\]
不过要求\(j\)还没有这一位，否则会有重复导致计数出错
然后结束
其实还没有
你会发现转移只是从\(i-1\)转移而来，并且都是小的状态更新大的状态，于是我们就可以把第一维压掉并且倒序枚举
在常数上有了巨大的优化
结束
AC代码
#define abhwolxq bailan
#define WWW signed
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#define M 300005
#define fre(x) freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define ll long long
using namespace std;
inline int Max(int a, int b) { return a > b ? a : b; }
inline int Min(int a, int b) { return a < b ? a : b; }
inline ll read() {
ll x = 0;
bool f = false;
char c = getchar();
while(!isdigit(c)) {
if (c == '-') f = true;
c = getchar();
}
do {
x = (x << 1) + (x << 3) + (c ^ 48);
}while(isdigit(c = getchar()));
if (f) return -x;
return x;
}
int n, k, S, a[M], ans = 1919810, len[M], f[100005];
WWW main() {
n = read(); k = read(); S = 1 << k; S--;
for (int i = 1; i <= n; i++) a[i] = read();
for (int i = 1; i <= S; i++) len[i] = len[i >> 1] + (i & 1);
memset(f, 50, sizeof(f));
f[0] = 0;
for (int i = 1; i <= n; i++) {
for (int j = S; j >= 0; j--) {
int t = 1 << a[i] - 1;
if (!(j & t)) f[j | t] = Min(f[j | t], f[j] + len[j >> a[i]]);
f[j] += Min(len[j], len[S ^ j]);
}
}
printf("%d", f[S]);
return 0;
}
15 9/26 CSP-S模拟12 T2 叁仟柒佰万
依旧是一道D
求划分序列且每个区间\(mex\)相同的方案数
先考虑这个\(mex\)是什么，最终的\(mex\)一定是原序列的\(mex\)
证明
假设现在划分好了区间且\(mex_k\)相同并小于原序列的\(mex\)，那么因为必然存在至少一个数为\(mex_k+1\)，且存在于一个区间里面，那么这个区间的\(mex\)增加
故重复这个过程必然会让\(mex_k\)到达区间的\(mex\)
证毕
那么设\(f_i\)为到第\(i\)个位置的方案数，则转移式子为
\[f_i = \sum_{j,mex(j + 1,i)=mex(1,n)}f_j
\]
然后我们可以预处理出所有的\(mex\)进行\(O(n^2)\)的转移
考虑优化
可以发现当\(i\)增大时\(j\)是单调递增的，所以我们可以用桶，双指针和前缀和直接进行\(O(n)\)的转移
结束
AC代码
#define abhwolxq bailan
#define WWW signed
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <random>
#define M 37000005
#define fre(x) freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define ll long long
#define mod 1000000007
using namespace std;
int wrt[20], TP;
inline int Max(int a, int b) { return a > b ? a : b; } inline int Min(int a, int b) { return a < b ? a : b; }
inline int read() {int x = 0;bool f = false;char c = getchar();while(!isdigit(c)){if (c == '-') f = true;c = getchar();}do {x = (x << 1) + (x << 3) + (c ^ 48);}while(isdigit(c = getchar()));if (f) return -x;return x;}
inline void write(int x) {TP = 0;if (x < 0) putchar('-'), x = -x;while(x >= 10) wrt[++TP] = x % 10, x /= 10; wrt[++TP] = x;while(TP) putchar(wrt[TP--] | 48); putchar('\n');}
int n, a[M], f[M], t[M];
bool vis[M];
void lbwnb() {
int x = read(), y = read();
a[1] = 0;
for (int i = 2; i <= n; i++) a[i] = (ll)(a[i - 1] * x + y + i) & 262143;
}
WWW main() {
int T = read();
while(T--) {
n = read();
if (n == 37000000) lbwnb();
else for (int i = 1; i <= n; i++) a[i] = read();
int mex = 0;
for (int i = 1; i <= n; i++) {
vis[a[i]] = 1;
while(vis[mex]) mex++;
}
int l = 1, r = 0, now = 0;
while(now < mex) {
t[a[++r]]++;
while(t[now]) now++;
}
ll sum = 1; f[r] = sum;
for (int i = r + 1; i <= n; i++) {
if (a[i] < mex) t[a[i]]++;
while(l < i) {
if (a[l] > mex) { (sum += f[l++]) %= mod; continue; }
if (t[a[l]] > 1) { t[a[l]]--, (sum += f[l++]) %= mod; continue; }
else break;
}
f[i] = sum;
}
printf("%d\n", f[n]);
for (int i = 0; i <= n; i++) f[i] = vis[i] = t[i] = 0;
}
return 0;
}
16 9/26 CSP-S模拟12 T3 超级加倍
笛卡尔树重构题
具体是个什么东西就不在这说了，这里有
考虑在这个题里面怎么用
对原树进行一个笛卡尔树的重构，一棵大根堆，一棵小根堆
以大根堆为例，重构的方法就是从小到大依次考虑每个点的每条边，如果指向的点比自己小，那么自己向这个点在并查集中的根连边，小根堆反过来就可以了
那么能对答案产生贡献的点对在两棵树上互为祖先
所以先对第一棵树跑\(dfs\)序，记录自己和子树的时间戳
然后对另一棵数一样跑一遍\(dfs\)，到了这个点就在它自己的时间上放到树状数组里，然后查询它子树这段时间内有多少个点即可
结束
AC代码
#define abhwolxq bailan
#define WWW signed
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <random>
#define M 2000005
#define fre(x) freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define ll long long
#define int long long
#define mod 1000000007
using namespace std;
int wrt[20], TP;
inline int Max(int a, int b) { return a > b ? a : b; } inline int Min(int a, int b) { return a < b ? a : b; }
inline int read() {int x = 0;bool f = false;char c = getchar();while(!isdigit(c)){if (c == '-') f = true;c = getchar();}do {x = (x << 1) + (x << 3) + (c ^ 48);}while(isdigit(c = getchar()));if (f) return -x;return x;}
inline void write(int x) {TP = 0;if (x < 0) putchar('-'), x = -x;while(x >= 10) wrt[++TP] = x % 10, x /= 10; wrt[++TP] = x;while(TP) putchar(wrt[TP--] | 48); putchar('\n');}
int n, a[M]; ll ans;
struct Gragh {
struct edge { int v, next; }e[M << 1];
int head[M], tot = 1, rt;
void add(int u, int v) { e[tot].v = v, e[tot].next = head[u], head[u] = tot++; }
}E, B, G;
struct bjc {
int f[M];
void init() { for (int i = 1; i <= n; i++) f[i] = i; }
inline int find(int x) { return f[x] == x ? x : f[x] = find(f[x]); }
void un(int x, int y) { f[find(y)] = find(x); }
}F;
struct treesz {
ll c[M];
#define low_bit (x & -x)
void updata(int x, int val) { while(x <= n) c[x] += val, x += low_bit; }
ll query(int x) { ll res = 0; while(x) res += c[x], x -= low_bit; return res; }
}C;
int mx[M], mn[M], tim;
void dfs1(int x) {
mn[x] = ++tim;
for (int i = B.head[x]; i; i = B.e[i].next) {
int v = B.e[i].v;
dfs1(v);
}
mx[x] = tim;
}
void dfs2(int x) {
C.updata(mn[x], 1);
ans += C.query(mx[x]) - C.query(mn[x]);
for (int i = G.head[x]; i; i = G.e[i].next) {
int v = G.e[i].v;
dfs2(v);
}
C.updata(mn[x], -1);
}
WWW main() {
n = read(); read();
for (int i = 2; i <= n; i++) {
int x = read();
E.add(i, x), E.add(x, i);
}
F.init();
for (int x = 1; x <= n; x++) {
for (int i = E.head[x]; i; i = E.e[i].next) {
int v = E.e[i].v;
if (v > x) continue;//建一棵大根堆的笛卡尔树
B.add(x, F.find(v)); F.un(x, v);
}
}
B.rt = F.find(1); F.init();
for (int x = n; x >= 1; x--) {
for (int i = E.head[x]; i; i = E.e[i].next) {
int v = E.e[i].v;
if (v < x) continue;//小根堆
G.add(x, F.find(v)); F.un(x, v);
}
}
G.rt = F.find(1);
dfs1(B.rt), tim = 0, dfs2(G.rt);
printf("%lld", ans);
return 0;
}
17 10/12 CSP-S模拟18 T2 2A+x
思维题
如果确定了操作次数\(k\)，那么一个数相当与对应了一个区间\([a_i 2^k,s_i 2^k+x(2^k-1)]\)
那么答案就是\(maxl-minr\)
先对原\(a\)排个序，让所有的\(a\)都接近\(maxa\)，如果区间覆盖了\(maxa\)的话，这个数就没有意义了
否则的话记录操作次数和右端点
此时如果\(minr\)与\(maxa\)的差小于\(x\)，则可以通过调整让距离缩掉，答案就是\(0\)
否则分讨：
一种是不再进行操作，答案就是\(maxl-minr\)
一种是考虑进行操作，枚举操作断点，\(1~i\)这一段直接乘\(2\)取\(maxl\)，在\(i+1~n\)这一段取\(minr\)来更新答案
最后一种就是考虑目前最小答案的\(maxl\)和\(minr\)，进行\(minr\times2+x\)，\(maxr\times2\)，如果此时答案缩小了，则我可以通过不断操作让答案最终变成0，否则取\(min\)即可
结束
AC代码
#define abhwolxq bailan
#define WWW signed
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#define M 100005
#define ll long long
#define int long long
#define inf 1000000000000000000
#define fre(x) freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define fin(x) freopen(#x ".in", "r", stdin)
#define rep(i, a, b) for (int (i) = (a); (i) <= (b); (i)++)
#define dwn(i, a, b) for (int (i) = (a); (i) >= (b); (i)--)
using namespace std;
int wrt[20],TP;
inline int Min(int a, int b) { return a < b ? a : b; } inline int Max(int a, int b) { return a > b ? a : b; }
inline int read() {int x = 0;bool f = false;char c = getchar();while(!isdigit(c)) {if (c == '-') f = true;c = getchar();}do {x = (x << 1) + (x << 3) + (c ^ 48); }while(isdigit(c = getchar()));if (f) return -x;return x;}
inline void print(int x, bool op) {TP = 0;if (x < 0) putchar('-'), x = -x;while(x >= 10) wrt[++TP] = x % 10, x /= 10; putchar(x | 48);while(TP) putchar(wrt[TP--] | 48);if (op) putchar('\n'); else putchar(' ');}
int n, x; ll mi[60], ans = inf;
struct node {
int a, k, r;
friend bool operator< (const node &A, const node &B) { return A.a < B.a; }
}a[M];
WWW main() {
mi[0] = 1;
rep(i, 1, 50) mi[i] = mi[i - 1] * 2;
n = read(), x = read();
rep(i, 1, n) a[i].a = read();
sort(a + 1, a + 1 + n);
rep(i, 1, n) {
a[i].k = log2(a[n].a / a[i].a);//不用x需要多少步才能跳到最大的a
a[i].a *= mi[a[i].k];
if (a[i].a + (mi[a[i].k] - 1) * x >= a[n].a) a[i].a = a[n].a, a[i].k = 0;
a[i].r = a[i].a + x * (mi[a[i].k] - 1);
}
sort(a + 1, a + 1 + n);
int maxr = inf;
rep(i, 1, n) maxr = Min(maxr, a[i].r);
if (a[n].a - maxr < x) { print(0, 0); return 0; }
ans = Min(ans, a[n].a - maxr);
maxr = a[n].r;
dwn(i, n, 1) {
ans = Min(ans, 2 * a[i].a - maxr);
maxr = Min(maxr, a[i].r);
}
print(Min(ans, a[n].a - a[1].a), 0);
}
18 10/12 CSP-S模拟18 T3 No Rest for the Wicked
用线段树分治实现D
定义\(f_{x,v}\)为\(c\)为\(x\)经过\(v\)的最大观赏度，然后可以\(O(n^2)\)转移
考虑边\((u,v)\)，当\(x\in[max(c_u, c_v),min(t_u,t_v)]\)时，这条边是可以随便通行的
而设\(c_u < c_v\)，当\(x \in [c_u,min(c_v-1,t_u)]\)时，我只能从\(u\)->\(v\)，所以我在\(u\)点可以直接继承\(v\)点的答案
然后你就可以发现所有的边有了范围，我们就可以进行线段树分治了
结束
AC代码
#define abhwolxq bailan
#define WWW signed
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <vector>
#define M 500005
#define ll long long
#define fre(x) freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define fin(x) freopen(#x ".in", "r", stdin)
#define rep(i, a, b) for (int (i) = (a); (i) <= (b); (i)++)
#define dwn(i, a, b) for (int (i) = (a); (i) >= (b); (i)--)
using namespace std;
int wrt[20],TP;
inline int Min(int a, int b) { return a < b ? a : b; } inline int Max(int a, int b) { return a > b ? a : b; }
inline int read() {int x = 0;bool f = false;char c = getchar();while(!isdigit(c)) {if (c == '-') f = true;c = getchar();}do {x = (x << 1) + (x << 3) + (c ^ 48); }while(isdigit(c = getchar()));if (f) return -x;return x;}
inline void print(int x, bool op) {TP = 0;if (x < 0) putchar('-'), x = -x;while(x >= 10) wrt[++TP] = x % 10, x /= 10; putchar(x | 48);while(TP) putchar(wrt[TP--] | 48);if (op) putchar('\n'); else putchar(' ');}
int n, m, c[M], t[M], f[M], siz[M], val[M], ans[M], top, lsh[M << 1], res;
inline int find(int x) { return f[x] == x ? x : find(f[x]); }
struct node { bool op; int x, fa, val; }stk[M << 3];
struct edge { int u, v; }e[M];
vector<int> ck[M];
vector<int> d[M << 2], s[M << 2];
#define ls (rt << 1)
#define rs ((rt << 1) | 1)
void updata(int rt, int l, int r, int L, int R, int id, bool op) {
if (L <= l and r <= R) { if (op) d[rt].push_back(id); else s[rt].push_back(id); return; }
int mid = l + r >> 1;
if (L <= mid) updata(ls, l, mid, L, R, id, op);
if (R > mid) updata(rs, mid + 1, r, L, R, id, op);
}
void solve(int rt, int l, int r) {
int st = top;
for (int i = 0; i < s[rt].size(); i++) {
int u = e[s[rt][i]].u, v = e[s[rt][i]].v;
int fu = find(u), fv = find(v);
if (fu == fv) continue;
if (siz[fu] < siz[fv]) swap(fu, fv);
stk[++top] = (node){0, fv, fu, val[fu]};
val[fu] = Max(val[fu], val[fv]), siz[fu] += siz[fv], f[fv] = fu;
}
for (int i = 0; i < d[rt].size(); i++) {
int u = e[d[rt][i]].u, v = e[d[rt][i]].v;
int fu = find(u), fv = find(v);
stk[++top] = (node){1, fu, 0, val[fu]};
val[fu] = Max(val[fu], ans[fv]);
}
if (l == r) for (int i = 0; i < ck[l].size(); i++) ans[ck[l][i]] = val[find(ck[l][i])];
else {
int mid = l + r >> 1;
solve(rs, mid + 1, r), solve(ls, l, mid);
}
while(top > st) {
int u = stk[top].x, fa = stk[top].fa;
if (stk[top].op) val[u] = stk[top].val;
else f[u] = u, val[fa] = stk[top].val, siz[fa] -= siz[u];
top--;
}
}
WWW main() {
n = read(), m = read();
rep(i, 1, n) lsh[++res] = c[i] = read(), lsh[++res] = t[i] = read(), ans[i] = val[i] = read();
sort(lsh + 1, lsh + 1 + res);
int cnt = unique(lsh + 1, lsh + 1 + res) - lsh - 1;
rep(i, 1, n) {
f[i] = i; siz[i] = 1;
c[i] = lower_bound(lsh + 1, lsh + 1 + cnt, c[i]) - lsh;
t[i] = lower_bound(lsh + 1, lsh + 1 + cnt, t[i]) - lsh;
ck[c[i]].push_back(i);
}
rep(i, 1, m) {
int u = read(), v = read();
if (c[u] > c[v]) swap(u, v);
updata(1, 1, cnt, c[v], min(t[u], t[v]), i, 0);
if (c[u] <= c[v] - 1) updata(1, 1, cnt, c[u], min(c[v] - 1, t[u]), i, 1);
e[i].u = u, e[i].v = v;
}
solve(1, 1, cnt);
rep(i, 1, n) print(ans[i], 0);
return 0;
}
19 10/12 CSP-S模拟18 T4 暴力题
线段树，但是很狗
原式子为\(\sum_{i=1}^{n}{\lfloor \frac{b_i\times i^k}{w} \rfloor}\)
把向下取整去掉\(\frac{\sum_{i=1}^{n}{b_i\times i^k}-\sum_{i=1}^{n}{b_i\times i^k \% w}}{w}\)
所以我们只需要维护上面这两项最后乘上逆元即可
在权值线段树中维护\(f_i\)和\(cnt_{i,j}\)，\(f_i = \sum_{j=1}^{sum}{b_j \times j^i}\)，\(cnt_{x,y}\)代表了\(b\%w\)为\(x\)，\(i\%w\)为\(y\)的个数
然后合并节点的时候，左儿子贡献不变，而右儿子需要在原有基础上向右推上左儿子的个数
设左儿子有\(a\)个，则右儿子的贡献成为
\[\sum_{i=1}^{sum}{b_i \times (i+a)^k}
\]
用二项式定理进行化简
\[\sum_{i=1}^{sum}{b_i \times \sum_{t=0}^{k} \binom{k}{t} \times i^k \times a^{k-t}}
\]
换一下枚举顺序
\[\sum_{t=0}^{k}{\sum_{i=1}^{sum}b_i \times i^k \times \binom{k}{t} \times a^{k-t}}
\]
\[\sum_{t=0}^{k}{f_k \times \binom{k}{t} \times a^{k-t}}
\]
然后就可以\(O(k^2)\)转移了
而对于\(cnt\)暴力\(O(w^2)\)转移即可
复杂度是\(O((n+q)\times (k^2 + w^2)\times log1e5)\)的
结束
AC代码
#define abhwolxq bailan
#define WWW signed
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#define M 100005
#define ll long long
#define int long long
#define mod 998244353
#define fre(x) freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define fin(x) freopen(#x ".in", "r", stdin)
#define rep(i, a, b) for (int (i) = (a); (i) <= (b); (i)++)
#define dwn(i, a, b) for (int (i) = (a); (i) >= (b); (i)--)
using namespace std;
int wrt[20],TP;
inline int Min(int a, int b) { return a < b ? a : b; } inline int Max(int a, int b) { return a > b ? a : b; }
inline int read() {int x = 0;bool f = false;char c = getchar();while(!isdigit(c)) {if (c == '-') f = true;c = getchar();}do {x = (x << 1) + (x << 3) + (c ^ 48); }while(isdigit(c = getchar()));if (f) return -x;return x;}
inline void print(int x, bool op) {TP = 0;if (x < 0) putchar('-'), x = -x;while(x >= 10) wrt[++TP] = x % 10, x /= 10; putchar(x | 48);while(TP) putchar(wrt[TP--] | 48);if (op) putchar('\n'); else putchar(' ');}
inline int qbow(int a, int b, int p) {int res = 1;while(b) {if (b & 1) res = res * a % p;a = a * a % p;b >>= 1;}return res;}
int n, k, w, a[M], c[6][6];
struct tree {
int sum, cnt[6][6], f[6];
#define ls (rt << 1)
#define rs ((rt << 1) | 1)
}e[M << 2];
void pushup(int rt) {
e[rt].sum = e[ls].sum + e[rs].sum;
rep(i, 0, k) {
e[rt].f[i] = e[ls].f[i];
rep(j, 0, i) (e[rt].f[i] += e[rs].f[j] * c[i][j] % mod * qbow(e[ls].sum, i - j, mod) % mod) %= mod;
}
rep(i, 0, w) rep(j, 0, w) e[rt].cnt[i][j] = e[ls].cnt[i][j];
rep(i, 0, w) rep(j, 0, w) (e[rt].cnt[i][(j + e[ls].sum) % w] += e[rs].cnt[i][j]) %= mod;
}
void updata(int rt, int l, int r, int pos, int val) {
if (l == r) {
e[rt].sum += val;
rep(i, 0, k) (e[rt].f[i] += val * l % mod * qbow(e[rt].sum + (val == -1), i, mod) % mod) %= mod;
e[rt].cnt[l % w][(e[rt].sum + (val == -1)) % w] += val;
return;
}
int mid = l + r >> 1;
if (pos <= mid) updata(ls, l, mid, pos, val);
else updata(rs, mid + 1, r, pos, val);
pushup(rt);
}
WWW main() {
n = read(), k = read(), w = read();
c[0][0] = 1;
rep(i, 1, 5) { c[i][0] = 1; rep(j, 1, i) c[i][j] = c[i - 1][j] + c[i - 1][j - 1]; }
rep(i, 1, n) a[i] = read(), updata(1, 0, 100000, a[i], 1);
int T = read(), ny = qbow(w, mod - 2, mod);
while(T--) {
int pos = read(), x = read();
updata(1, 0, 100000, a[pos], -1);
updata(1, 0, 100000, x, 1);
a[pos] = x;
int ans = e[1].f[k], y = 0;
rep(i, 0, w) rep(j, 0, w) (y += (i * qbow(j, k, w) % w) * e[1].cnt[i][j] % mod) %= mod;
print((ans - y + mod) * ny % mod, 1);
}
return 0;
}
20 10/15 多校 T2 vmefifty
是一道原题，不过当时我不在所以没做
又是一道D
首先考虑因为每次消去两个数且两个数必须不同，所以一个区间可以被完全消掉的条件是区间长度为偶数并且区间不存在绝对众数即众数出现次数不超过区间长度的一半
定义\(qj_{i, j}\)代表区间\([i,j]\)能否被消掉
定义\(f_i\)以第\(i\)个位置为结尾且只剩下\(a_i\)的最长区间长度
那么只要满足了\(a_i = a_j\)和\(qj_{j+1, i-1} = 1\)就能从\(j\)转移到\(i\)
则\(f_i = f_j + 1\)
转移就是\(O(n^2)\)的
统计答案时只要满足\(qj_{i+1,n}=1\)，那么位置\(i\)就是合法的
所以\(ans = max(ans, f_i)\)
结束
点击查看代码
#define abhwolxq bailan
#define WWW signed
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <cstring>
#define M 5005
#define ll long long
#define inf 114514
#define fre(x) freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define fin(x) freopen(#x ".in", "r", stdin)
#define rep(i, a, b) for (int (i) = (a); (i) <= (b); (i)++)
#define dwn(i, a, b) for (int (i) = (a); (i) >= (b); (i)--)
using namespace std;
int wrt[20], TP;
inline int Min(int a, int b) { return a < b ? a : b; } inline int Max(int a, int b) { return a > b ? a : b; }
inline int read() {int x = 0; bool f = false;char c = getchar();while(!isdigit(c)) {if (c == '-') f = true;c = getchar();}do {x = (x << 1) + (x << 3) + (c ^ 48);}while(isdigit(c = getchar()));if (f) return -x;return x;}
inline void print(int x, bool op) {TP = 0; if (x < 0) x = -x, putchar('-');while(x >= 10) wrt[++TP] = x % 10, x /= 10; putchar(x | 48);while(TP) putchar(wrt[TP--] | 48); if (op) putchar('\n'); else putchar(' ');}
int n, a[M], f[M], t[M];
bool qj[M][M];
WWW main() {
int T = read();
while(T--) {
n = read();
rep(i, 1, n) a[i] = read();
rep(i, 0, n) qj[0][i] = 1;
rep(i, 1, n) {
int maxn = 0;
rep(j, 1, n) t[j] = 0;
dwn(j, i - 1, 0) qj[i][j] = 1;
rep(j, i, n) {
t[a[j]]++;
if (t[a[j]] > t[maxn]) maxn = a[j];
if (!((j - i + 1) & 1) and t[maxn] * 2 <= j - i + 1) qj[i][j] = 1;
}
}
int ans = 0;
rep(i, 1, n) {
if (!qj[1][i - 1] and i != 1) f[i] = -inf;
else f[i] = 1;
dwn(j, i - 1, 0) if (qj[j + 1][i - 1] and a[i] == a[j]) f[i] = Max(f[i], f[j] + 1);
if (qj[i + 1][n] or i == n) ans = Max(ans, f[i]);
}
print(n - ans, 1);
if (T) rep(i, 0, n) rep(j, 0, n) qj[i][j] = 0;
}
return 0;
}
