考试杂写1
由于没有写完整题解的时间以及那个毅力
我选择杂写
并非按照时间顺序，只能说是乱jb写
题面挂了链接，不知道的你也进不去
1.10/02多校 T1 二分图排列
个人认为难度大概是T3，赛时断断续续搞了好久（其实全是扯淡）
因为每个逆序对都要连边，所以我会和所有我前面的比我大的连边
那么如果取反，则我直接和在原序列中比我小的连边
又因为要求二分图，所以不能有奇环，所以不能有长度大于2的下降子序列（赛时就到这了）
于是可以得出结论：
构造之后的序列只有能够分成两个上升子序列，才可以构造出合法方案
开D
为了后面方便贪心的构造。我们选择倒序D
定义\(f_{i, 0/1}\)为到\(i\)这个位置，\(0 / 1\)代表\(a_{i}\)取正还是负，另一个序列的最大结尾值
所以转移到\(i\)的时候我考虑四个值\(a_{i+1}, -a_{i+1}, f_{i+1, 0}, f_{i+1, 1}\)能不能接到我\(i\)的后面
只要这四个值大于我的\(a_{i}\)或者\(-a_{i}\)，我就可以对应着将\(f_{i+1, 0}, f_{i+1, 1}, a_{i+1}, -a_{i+1}\)放在另一个序列中，就能转移过来取\(max\)
全部初始化成极小值，如果\(0/1\)两个状态都没有被更新，则无解
考虑在有解情况下贪心构造
维护两个值\(now1\)和\(now2\)代表我两个上升子序列目前值是什么
因为字典序最小，能负就负，不能负就正，配合\(f\)判断能否选
AC代码
#define abhwolxq bailan
#define WWW signed
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <queue>
#define M 505
#define ll long long
#define fre(x) freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define rep(i, a, b) for (int (i) = (a); (i) <= (b); (i)++)
#define dwn(i, a, b) for (int (i) = (a); (i) >= (b); (i)--)
#define inf 2147483647
using namespace std;
int wrt[20], TP;
inline int Min(int a, int b) { return a < b ? a : b; } inline int Max(int a, int b) { return a > b ? a : b; }
inline int read() {int x = 0;bool f = false;char c = getchar();while(!isdigit(c)) {if (c == '-') f = true;c = getchar();}do {x = (x << 1) + (x << 3) + (c ^ 48);}while(isdigit(c = getchar()));if (f) return -x;return x;}
inline void print(int x, bool op) {TP = 0;if (x < 0) putchar('-'), x = -x;while(x >= 10) wrt[++TP] = x % 10, x /= 10; wrt[++TP] = x;while(TP) putchar(wrt[TP--] | 48);if (op) putchar('\n'); else putchar(' ');}
inline int qbow(int a, int b, int p) {int res = 1;while(b) {if (b & 1) res = res * a % p;a = a * a % p;b >>= 1;}return res;}
int n, a[M], f[M][2];
WWW main() {
int T = read();
while(T--) {
n = read(); bool op = true;
rep(i, 1, n) a[i] = read(), f[i][0] = f[i][1] = -inf;
f[n + 1][0] = f[n + 1][1] = a[n + 1] = inf;
dwn(i, n, 1) {
rep(j, 0, 1) {
int x = j ? -a[i] : a[i];
if (a[i + 1] > x) f[i][j] = Max(f[i][j], f[i + 1][0]);
if (-a[i + 1] > x) f[i][j] = Max(f[i][j], f[i + 1][1]);
if (f[i + 1][0] > x) f[i][j] = Max(f[i][j], a[i + 1]);
if (f[i + 1][1] > x) f[i][j] = Max(f[i][j], -a[i + 1]);
}
if (f[i][0] == -inf and f[i][1] == -inf) { op = false; break; }
}
if (!op) { puts("NO"); continue; }
else puts("YES");
int now1 = -inf, now2 = -inf;
rep(i, 1, n) {
if (-a[i] > now1) now1 = -a[i], print(-a[i], 0);
else if (-a[i] > now2 && -a[i] < f[i][1]) now2 = -a[i], print(-a[i], 0);
else now1 = a[i], print(a[i], 0);
if (now1 < now2) swap(now1, now2);
}
putchar('\n');
}
return 0;
}
2. 10/02多校 T2 最短路问题 V3
这个题不难，放在T1比较合适（没切的我是彩笔）
观察数据范围 $$ n - 1 \le m \le n + 20 $$
这个很奇特，令人不由自主的就觉得有问题
那么我们由此入手
对原图跑一棵生成树出来，顺便剖掉
那么在树上询问两点距离直接\(lca\)即可
但是由于非树边的存在导致最短路可能更短
那么我们对每条非树边的两点进行一个\(dij\)的跑
因为非树边很少，最多\(42\)个，所以没问题
每个询问的时候再遍历每个特殊点和\(ans\)取\(min\)即可
写个题的原因就是好好看数据范围，知道有不对劲的东西就尽力深挖
正解大概率相关
3. 10/01 国庆のsurprise T2 Su_Zipei is always here
呃呃
无事发生
一道根号分治，似乎暑假的时候有一道，不过忘掉了
为了方便描述，我们定义出现次数多于\(\sqrt{n}\)的元素为重要元素
而少于\(\sqrt{n}\)次的元素为普遍元素
可以发现，重要元素的数量一定少于\(\sqrt{n}\)个，而普遍元素的数量虽然多于\(\sqrt{n}\)个，但是单种元素的数量少于\(\sqrt{n}\)个
于是我们针对两个少于\(\sqrt{n}\)的特性进行分治
在时间和空间上达到\(O(n\sqrt{n})\)的效率
AC代码
#define abhwolxq bailan
#define WWW signed
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#define M 100005
#define fre(x) freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define ll long long
#define rep(i, a, b) for (int (i) = (a); (i) <= (b); (i)++)
#define dwn(i, a, b) for (int (i) = (a); (i) >= (b); (i)--)
using namespace std;
int wrt[20], TP;
inline int Min(int a, int b) { return a < b ? a : b; } inline int Max(int a, int b) { return a > b? a : b; }
inline int read() {int x = 0;bool f = false;char c = getchar();while(!isdigit(c)) {if (c == '-') f = true;c = getchar();}do {x = (x << 1) + (x << 3) + (c ^ 48);}while(isdigit(c = getchar()));if (f) return -x;return x;}
inline void print(int x, bool op) {TP = 0;if (x < 0) x = -x, putchar('-');while(x >= 10) wrt[++TP] = x % 10, x /= 10;wrt[++TP] = x; while(TP) putchar(wrt[TP--] | 48); if (op) putchar('\n'); else putchar(' ');}
int n, m, q, opt, a[M], st[M], ed[M], bl[M];
int pos[320][M], bh[M], num;//第i种重要元素在前j个位置有多少个
int sum[320][M];//前i块元素为j的数量
int tot[320][320][320];//[i， j]块内出现大于等于k次的元素数量
int cnt[M];//桶
void fk() {
rep(i, 1, q) st[i] = ed[i - 1] + 1, ed[i] = n / q * i;
if (ed[q] != n) st[q + 1] = ed[q] + 1, ed[++q] = n;
rep(i, 1, q) rep(j, st[i], ed[i]) bl[j] = i;
rep(i, 1, n) cnt[a[i]]++;
rep(i, 1, n) if (cnt[i] > q) bh[i] = ++num;
rep(i, 1, n) cnt[a[i]] = 0;
rep(i, 1, n) if (bh[a[i]]) pos[bh[a[i]]][i]++;
rep(i, 1, num) rep(j, 1, n) pos[i][j] += pos[i][j - 1];//对重要元素的处理,O(nsqrtn)
rep(i, 1, q) {
rep(j, st[i], ed[i]) if (!bh[a[j]]) sum[i][a[j]]++;
rep(j, 1, n) sum[i][j] += sum[i - 1][j];
}
rep(i, 1, q) {
rep(j, i, q) {
rep(k, 1, q) tot[i][j][k] = tot[i][j - 1][k];
rep(k, st[j], ed[j]) {
if (!bh[a[k]]) {
tot[i][j][cnt[a[k]]]--;
tot[i][j][++cnt[a[k]]]++;
}
}
}
rep(k, 1, n) cnt[k] = 0;
}
rep(i, 1, q) rep(j, i, q) dwn(k, q, 1) tot[i][j][k] += tot[i][j][k + 1];//对普遍元素的处理,O(nsqrtn)
}
inline int query(int l, int r, int k) {
int res = 0;
if (bl[r] - bl[l] < 2) {
rep(i, l, r) {
cnt[a[i]]++;
if (cnt[a[i]] == k) res++;
}
rep(i, l, r) cnt[a[i]] = 0;
}else {
if (k <= q) res = tot[bl[l] + 1][bl[r] - 1][k];//小于根号直接先统计一把
rep(i, l, ed[bl[l]]) {
if (!bh[a[i]]) {
cnt[a[i]]++;
if (cnt[a[i]] + sum[bl[r] - 1][a[i]] - sum[bl[l]][a[i]] == k) res++;
}
}
rep(i, st[bl[r]], r) {
if (!bh[a[i]]) {
cnt[a[i]]++;
if (cnt[a[i]] + sum[bl[r] - 1][a[i]] - sum[bl[l]][a[i]] == k) res++;
}
}
rep(i, l, ed[bl[l]]) cnt[a[i]] = 0; rep(i, st[bl[r]], r) cnt[a[i]] = 0;
rep(i, 1, num) if (pos[i][r] - pos[i][l - 1] >= k) res++;
}
return res;
}
WWW main() {
n = read(), m = read(), opt = read(); q = sqrt(n);
rep(i, 1, n) a[i] = read();
fk();
int ans = 0;
while(m--) {
int f = ans * opt - 1;
int l = (read() + f) % n + 1, r = (read() + f) % n + 1, k = (read() + f) % n + 1;
if(l > r) swap(l, r);
ans = query(l, r, k);
print(ans, 1);
}
return 0;
}
4. 9/30 CSP-S模拟15 T3 追逐
当我们固定一个起点后，把起点作为整个树的根，那么这时每个节点选不选的价值就是它所有儿子的铁球数量加和。
首先，树形dp还是比较好想且显然的
定义\(f_{u, i}\)代表我以\(u\)为根的子树中用过了\(i\)块磁铁的最大价值
考虑当前节点则转移为
而\(sum_{u}\)是\(u\)所有儿子的价值和
这样每个点作为树根跑一边\(dfs\)是\(O(n^2k)\)的，不过已经可以拿到\(70pts\)的好成绩了
(见到\(dp\)想都不想的我是屑)
所以我们考虑换根\(dp\)
在原\(dp\)数组的定义上，我们再加上一维\(0/1\)代表我当前节点有没有用磁铁
然后就有了\(g\)数组的定义：从非\(u\)的子树中转移而来的最大价值
只是转移路径变了，定义不变
通俗点的理解就是你把\(v\)节点当成根的话，除了他自己的子树，其余都会成为\(u\)的子树，\(v\)的儿子就是\(u\)，所以\(v\)节点更新答案的时候要考虑\(u\)这棵子树的贡献
看图
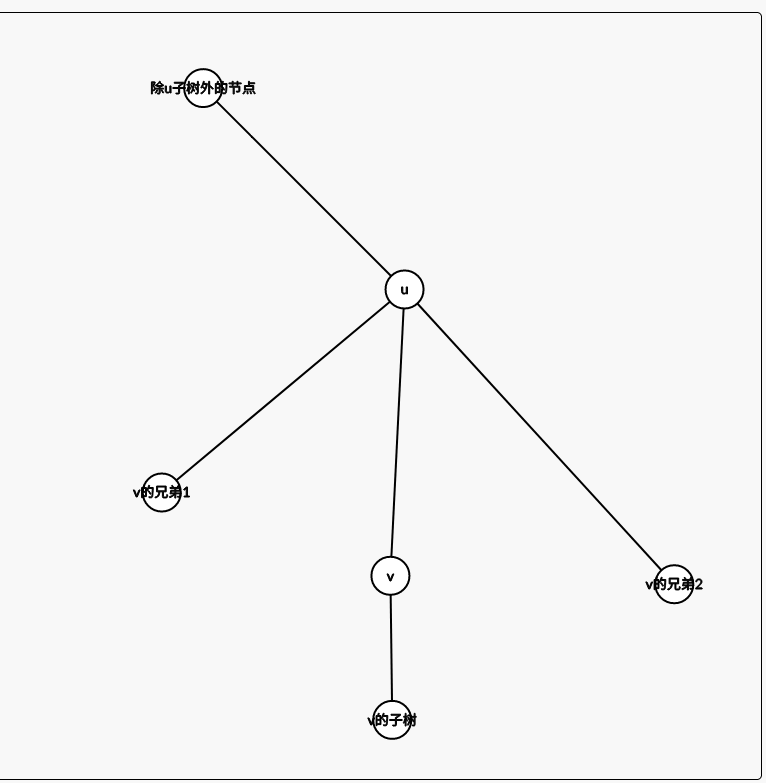
然后变成这样
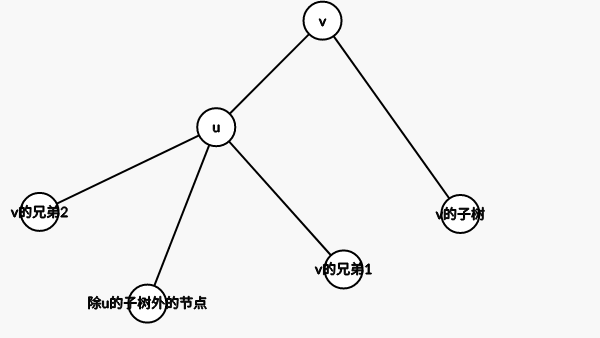
所以你相当就是用\(u\)节点的\(g\)数组更新\(v\)节点的\(g\)数组，更新方式和\(f\)一样，不过本来你\(u\)节点的\(f\)可能就是\(v\)转移而来的最大值，那么你就不能再用这个最大值更新\(v\)，这显然很扯淡
所以在第一次统计\(f\)数组的时候再维护一个转移来最大值和非严格次大值的节点，然后判断转移即可
结束
AC代码
#define abhwolxq bailan
#define WWW signed
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#define M 100005
#define fre(x) freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define ll long long
#define int long long
#define rep(i, a, b) for (int (i) = (a); (i) <= (b); (i)++)
#define dwn(i, a, b) for (int (i) = (a); (i) >= (b); (i)--)
using namespace std;
int wrt[20], TP;
inline ll Max(ll a, ll b) { return a > b ? a : b; }
inline int read() {int x = 0;bool f = false;char c = getchar();while(!isdigit(c)) {if (c == '-') f = true;c = getchar();}do {x = (x << 1) + (x << 3) + (c ^ 48);}while(isdigit(c = getchar()));if (f) return -x;return x;}
inline void print(int x, bool op) {TP = 0;if (x < 0) x = -x, putchar('-');while(x >= 10) wrt[++TP] = x % 10, x /= 10;wrt[++TP] = x; while(TP) putchar(wrt[TP--] | 48); if (op) putchar('\n'); else putchar(' ');}
int n, m, a[M]; ll sum[M], ans;
struct egde { int v, next; }e[M << 1];
int head[M], tot = 1;
void add(int u, int v) { e[tot].v = v, e[tot].next = head[u], head[u] = tot++; }
ll f[M][101][2], g[M][101][2];//原dp数组和换根dp数组
int mx[M][101][2], mn[M][101][2];//贡献最大值和次大值所在的节点
inline void updata(int rt, int v, int j, int op) {//记录最大值和次大值
if (f[mx[rt][j][op]][j][op] <= f[v][j][op]) mn[rt][j][op] = mx[rt][j][op], mx[rt][j][op] = v;
else if (f[mn[rt][j][op]][j][op] < f[v][j][op]) mn[rt][j][op] = v;
}
inline int query(int rt, int v, int j, int op) {
if (mx[rt][j][op] == v) return mn[rt][j][op];
return mx[rt][j][op];
}
void dfs1(int x, int fa) {
sum[x] = 0;
for (int i = head[x]; i; i = e[i].next) {
int v = e[i].v;
if (v == fa) continue;
dfs1(v, x); sum[x] += a[v];
}
rep(j, 0, m) {//枚举数量
for (int i = head[x]; i; i = e[i].next) {
int v = e[i].v;
if (v == fa) continue;
updata(x, v, j, 0), updata(x, v, j, 1);
f[x][j][0] = Max(f[x][j][0], Max(f[v][j][0], f[v][j][1]));
if (j) f[x][j][1] = Max(f[x][j][1], Max(f[v][j - 1][0], f[v][j - 1][1]) + sum[x]);
}
}
}
void dfs2(int x, int fa) {
ll mx0 = 0, mx1 = 0;
rep(j, 0, m) {//换根，考虑我如果以当前节点为根，那么也要考虑父亲一方的贡献
mx0 = Max(Max(g[fa][j][0], g[fa][j][1]), Max(f[mx[x][j][0]][j][0], f[mx[x][j][1]][j][1]));//当前节点不选
if (j) mx1 = Max(Max(g[fa][j - 1][0], g[fa][j - 1][1]), Max(f[mx[x][j - 1][0]][j - 1][0], f[mx[x][j - 1][1]][j - 1][1])) + sum[x] + a[fa];//当前节点选
ans = Max(ans, Max(mx0, mx1));
}
for (int i = head[x]; i; i = e[i].next) {
int v = e[i].v;
if (v == fa) continue;
rep(j, 0, m) {
mx0 = query(x, v, j, 0), mx1 = query(x, v, j, 1);
g[x][j][0] = Max(Max(g[fa][j][0], g[fa][j][1]), Max(f[mx0][j][0], f[mx1][j][1]));
if (j) {
mx0 = query(x, v, j - 1, 0), mx1 = query(x, v, j - 1, 1);
g[x][j][1] = Max(Max(g[fa][j - 1][0], g[fa][j - 1][1]), Max(f[mx0][j - 1][0], f[mx1][j - 1][1])) + sum[x] + a[fa] - a[v];
}
}
dfs2(v, x);
}
}
WWW main() {
n = read(), m = read();
rep(i, 1, n) a[i] = read();
rep(i, 2, n) { int u = read(), v = read(); add(u, v), add(v, u); }
dfs1(1, 0); dfs2(1, 0);
print(ans, 0);
return 0;
}
5. 9/29 CSP-S模拟14 T2 尽梨了
一个一眼看上去就很奇怪且不可做题
结论是一道组合数学，考虑怎么算贡献
因为一个\(a\)数组对行贡献，一个\(b\)数组对列贡献
并且属于只要有一个合法即可，所以我们考虑固定一位来算另一位的贡献
考虑枚举我有几列放\(1\),这个枚举是\(1 - n\)的
对于一行来讲，1的个数是一定的且可以预处理的
那么设\(sum_{i}\)表示第\(i\)行\(1\)的个数，\(s\)表示列中\(1\)的 个数
那么分成了三种情况：
对于\(sum_{i} < s\)的行，所有是\(1\)的列必须是\(1\)，这些状态与起来表示为\(pre_{s}\)
对于\(sum_{i} > s\)的行，所有是\(0\)的列必须是\(0\)，这些状态或起来表示为\(suf_{s}\)
那么显然只有\(pre_{s}\)&\(suf_{s} = pre_{s}\)且\(pre_{s} | suf_{s} = suf_{s}\)时，\(s\)才是合法的
那么考虑是否有\(sum_{i} = s\)的行考虑贡献
如果存在，那么就要满足每行状态一样，对答案的贡献就是\(2^{行数}\)
如果不存在，设\(cnt_{1}\)为\(pre_{s}\)中的\(1\)的个数，设\(cnt_{2}\)为\(suf_{s}\)中的\(1\)的个数 那么贡献是\((^{cnt_{2}-cnt_{1}} _ {s - cnt_{1}})\)
这个组合数的意义就是我目前要求放\(s\)列\(1\)，已经放了\(cnt_{1}\)个\(1\)，有\(cnt_{2}\)个位置能放\(1\)
然后用\(bitset\)维护即可
结束
AC代码
#define abhwolxq bailan
#define WWW signed
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <bitset>
#include <vector>
#define M 5005
#define fre(x) freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define ll long long
#define int long long
#define mod 998244353
#define rep(i, a, b) for (int (i) = (a); (i) <= (b); i++)
#define dwn(i, a, b) for (int (i) = (a); (i) >= (b); i--)
using namespace std;
int wrt[20], TP;
inline int Max(int a, int b) { return a > b ? a : b; } inline int Min(int a, int b) { return a < b ? a : b; }
inline int read() {int x = 0;bool f = false;char c = getchar();while(!isdigit(c)){if (c == '-') f = true;c = getchar();}do {x = (x << 1) + (x << 3) + (c ^ 48);}while(isdigit(c = getchar()));if (f) return -x;return x;}
inline void print(int x, int op) {TP = 0;if (x < 0) x = -x, putchar('-');while(x >= 10) wrt[++TP] = x % 10, x /= 10; wrt[++TP] = x;while(TP) putchar(wrt[TP--] | 48); if (op) putchar('\n'); else putchar(' ');}
inline int qbow(int a, int b, int p) {ll res = 1;while(b) {if (b & 1) res = res * a % p;a = a * a % p;b >>= 1;}return res;}
int n, res[M]; char s[M]; ll jc[M], inv[M], ans;
bitset<M> bt[M], b1[M], b2[M];
vector<int> v[M];
inline int C(int n, int m) {
if (n < m || n < 0 || m < 0) return 0;
return jc[n] * inv[n - m] % mod * inv[m] % mod;
}
WWW main() {
n = read(); jc[0] = inv[0] = 1;
rep(i, 1, n) jc[i] = jc[i - 1] * i % mod;
inv[n] = qbow(jc[n], mod - 2, mod);
dwn(i, n - 1, 1) inv[i] = inv[i + 1] * (i + 1) % mod;
rep(i, 1, n) {
scanf("%s", s + 1);
rep(j, 1, n) {
bt[i][j] = s[j] == '1' ? 1 : 0;
if (bt[i][j]) res[i]++;
}
v[res[i]].push_back(i);
}
rep(i, 1, n) {
b1[i] = b1[i - 1];
for (auto j : v[i]) b1[i] |= bt[j];
}
rep(i, 1, n) b2[n + 1][i] = 1;
dwn(i, n, 1) {
b2[i] = b2[i + 1];
for (auto j : v[i]) b2[i] &= bt[j];
}
rep(s, 0, n) {
if ((b1[s] | b2[s]) == b2[s]) {//b2选0的位置依旧是0代表没有冲突
if (v[s].size()) { (ans += qbow(2, v[s].size(), mod)) %= mod; continue; }
int k1 = b1[s].count(), k2 = b2[s].count();
(ans += C(k2 - k1, s - k1)) %= mod;
}
}
print(ans, 0);
return 0;
}
6. 9/22 CSP-S模拟9 T1 最长上升子序列
一道贪心的构造
考虑已经给出来的这个上升序列不变，我们往里面塞数
对于原序列
两个数中间的数不能放在两个数中间
并且要求了字典序最小，那么我们考虑贪心的进行构造
第一个数显然不能放比给出的第一个数更小的数，又要求字典序最小，那第一个数就放给出的第一个数
考虑第二个数要怎么放，如果放原序列第二个数肯定没问题，但为了字典序最小，我们决定放一个更小的数，越小越好，所以我们拿出一个还没有放过的最小且比上一个数要小的数放在这个位置，这样这个数不会被夹在两个数中间就不会有贡献
下一个数就再放我原序列的数即可
但是如果没有小的你就不放，因为你放了还不如不放（这片题解怎么这么多屁话）
因为你放了字典序肯定更大，所以就不放
最后所有剩下的数倒序甩到后面就行
结束
AC代码
#define abhwolxq bailan
#define WWW signed
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#define M 200005
#define fre(x) freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define ll long long
using namespace std;
inline int Max(int a, int b) {return a > b ? a : b;}
inline int read() {
int x = 0;
bool f = false;
char c = getchar();
while(!isdigit(c)) {
if (c == '-') f = true;
c = getchar();
}
do {
x = (x << 1) + (x << 3) + (c ^ 48);
}while(isdigit(c = getchar()));
if (f) return -x;
return x;
}
int n, k, a[M], v[M];
WWW main() {
n = read(); k = read();
for (int i = 1; i <= k; i++) a[i] = read(), v[a[i]] = i;
int j = 1;
for (int i = 1; i < k; i++) {
printf("%d ", a[i]);
while(v[j]) j++;
if (j < a[i]) {
printf("%d ", j);
v[j] = n + 1;
}
}
for (int i = n; !v[i]; i--) printf("%d ", i), v[i] = n + 1;
printf("%d ", a[k]);
for (int i = n; i >= 1; i--) if (!v[i]) printf("%d ", i);
return 0;
}
7. 9/22 CSP-S模拟9 T2 独特序列
一道D，求所有不重复子序列的方案
定义\(f_i\)为我目前放的序列以\(a_i\)结尾的方案数
那么转移就是\(f_i = \sum_{j=lst_{a_i}}^{i}{f_j} + [lst_i = 0]\)，而\(lst_i\)为\(i\)上一次出现的位置
意义很好理解，\(lst_i\)之前的我已经在\(lst_i\)接过一次了，再转移就重复了
用链表和树状数组维护即可
结束
AC代码
#define abhwolxq bailan
#define WWW signed
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#define M 200005
#define fre(x) freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define ll long long
#define mod 998244353
using namespace std;
inline int Max(int a, int b) {return a > b ? a : b;}
inline int read() {
int x = 0;
bool f = false;
char c = getchar();
while(!isdigit(c)) {
if (c == '-') f = true;
c = getchar();
}
do {
x = (x << 1) + (x << 3) + (c ^ 48);
}while(isdigit(c = getchar()));
if (f) return -x;
return x;
}
int n, a[M], lst[M], nxt[M], pre[M];//lst维护了最后一个位置，pre，nxt是指向了上下一个本元素的位置
ll c[M], f[M], ans;
#define low_bit (x & -x)
void updata(int x, ll val) { while(x <= n) (c[x] += val) %= mod, x += low_bit; }
ll getsum(int x) {
if (x <= 0) return 0;
ll res = 0;
while(x) (res += c[x]) %= mod, x -= low_bit;
return res;
}
WWW main() {
n = read();
for (int i = 1; i <= n; i++) {
a[i] = read();
if (lst[a[i]]) nxt[lst[a[i]]] = i, pre[i] = lst[a[i]];
lst[a[i]] = i;
}
updata(1, 1);
f[1] = 1;
if (!nxt[1]) ans++;
for (int i = 2; i <= n; i++) {
f[i] = (getsum(i - 1) - getsum(pre[i] - 1) + mod) % mod;
if (pre[i]) updata(pre[i], -f[pre[i]]); else f[i]++;
if (!nxt[i]) (ans += f[i]) %= mod;//这个元素结尾的所有贡献
updata(i, f[i]);
}
printf("%lld\n", ans);
return 0;
}
8. 9/22 CSP-S模拟9 T3 最大GCD
一个还算有意思的题
\(gcd \le max{a_i}\) 是显然的
如果\(K\)值允许我将\(a_i\)全都加到一个值，那么之后我就能让整个序列保持在一个数一起增加，这样\(gcd\)是最大的
那我们考虑如果不行捏，那不行的话，就很烦
我们先想一个暴力，暴力枚举\(gcd\)然后判断是否合法
\(\lfloor \frac{K + \sum{a_i}}{n} \rfloor\) 是\(gcd\)的上界
那么只要满足 \(\sum a_{i} \% gcd\le K\) 即可
此时你觉得数论分块可做，但是交上去T掉了
考虑一点数学知识，现在的复杂度凝固在了 \(\lceil\frac{a_i}{gcd} \rceil\) 上，这个东西和数论分块差不多，就是对于一段连续的值域上，这个式子的值是相同的
即在\(((k - 1) \times d, k \times d]\) 这一段区间内的值都是\(k\)
那么我们可以对\(a_i\)处理一个桶及桶的前缀和，这样就可以以\(O(\frac{maxn}{gcd})\)的效率完成每次验证
结束
AC代码
#define abhwolxq bailan
#define WWW signed
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#define M 300005
#define fre(x) freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define ll long long
using namespace std;
inline ll read() {
ll x = 0;
bool f = false;
char c = getchar();
while(!isdigit(c)) {
if (c == '-') f = true;
c = getchar();
}
do {
x = (x << 1) + (x << 3) + (c ^ 48);
}while(isdigit(c = getchar()));
if (f) return -x;
return x;
}
int n;
ll sum, avr, k, a[M];
WWW main() {
n = read(), sum = k = read();
for (int i = 1; i <= n; i++) a[i] = read(), sum += a[i];
avr = sum / n;
cerr << avr;
sort(a + 1, a + 1 + n);
for (ll s = avr; s >= 2; s--) {
ll f = 0; bool op = true;
for (int i = 1; i <= n; i++) {
f += (ll)ceil(1.0 * a[i] / s) * s - a[i];
if (f > k) { op = false; break; }
}
if (op) { printf("%lld", s); return 0; }
}
printf("1");
return 0;
}
9.10/08多校 T2 天☆堂
先想暴力，把所有的子串取出来按照字典序赋一个值，于是我们得到一个\(O(n^2)\)的序列，跑一个最长上升子序列即可
那么这个实在是太暴力了，虽然分并不少，但我们考虑优化
时间复杂度必须保证在\(O(n^2)\)之内，一个\(log\)也加不了（题解原话
我们先考虑一些事情，如果我选中了一个\(l\)作为左端点，那么随着我的\(r\)的增长字典序递增
所以对于一个固定的\(l\)选中的\(r\)一定是连续的，显然
考虑另外一个事情，我对于一个\(l\)一定选到\(n\)更优
证明这个东西也不难，如果后面有一个位置\(l'\)，如果它代表的串比\(l\)字典序大，那么我把\(l\)选满不会对后面选他造成影响，否则有一位字典序更小，或者就是\(l\)的前缀，因为我\(l\)靠前选的位置更多，所以选到\(n\)是最优的
最后一个事情，我比较两个串的字典序比较的到底是什么
是两个字符串的LCP后的第一个字符
那么只要我们处理出任意两个串的\(LCP\)就可以\(O(n^2)\)的转移了
设\(f_{i, j}\)为以\(i\)和\(j\)为起点的字串的\(LCP\)长度
那么我们倒序枚举，转移就很显然了
那么状态数从\(O(n^2)\)减少到了\(O(n)\)，暴力的转移即可
时间复杂度O(n^2)
结束
AC代码
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#define abhwolxq bailan
#define WWW signed
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#define M 5005
#define ll long long
#define fre(x) freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define fin(x) freopen(#x ".in", "r", stdin)
#define rep(i, a, b) for (register int (i) = (a); (i) <= (b); (i)++)
#define dwn(i, a, b) for (register int (i) = (a); (i) >= (b); (i)--)
using namespace std;
int wrt[20], TP;
inline int Max(int a, int b) { return a > b ? a : b; }
inline int read() {int x = 0;bool f = false;char c = getchar();while(!isdigit(c)) {if (c == '-') f = true;c = getchar();}do {x = (x << 1) + (x << 3) + (c ^ 48);}while(isdigit(c = getchar()));if (f) return -x;return x;}
inline void print(int x, bool op) {TP = 0;if (x < 0) x = -x, putchar('-');while(x >= 10) wrt[++TP] = x % 10, x /= 10; putchar(x | 48);while(TP) putchar(wrt[TP--] | 48); if (op) putchar('\n'); else putchar(' ');}
int n, f[M], pos[M][M]; char s[M];
WWW main() {
int T = read();
while(T--) {
n = read();
scanf("%s", s + 1);
dwn(i, n, 1) dwn(j, n, i) {
pos[i][j] = 0;
if (s[i] == s[j]) pos[i][j] = pos[i + 1][j + 1] + 1;
}
int ans = 0;
rep(i, 1, n) {
f[i] = n - i + 1;
rep(j, 1, i - 1) {
int zi = i + pos[j][i], zj = j + pos[j][i];
if (zi <= n and s[zi] > s[zj]) f[i] = Max(f[i], f[j] + n - zi + 1);
}
ans = Max(ans, f[i]);
}
print(ans, 1);
}
return 0;
}
10. 10/06多校 T4 D
期望D
评价是不想写高斯，所以我们选择递推
设\(f_n = 0\), \(f_i\)为有了前\(i-1\)位，第一次出现第\(i\)位的期望，则$$f_i = \frac{1}{2} f_{i + 1} + \frac{1}{2}f_{v_i} + 1$$
很好理解，就是有\(\frac{1}{2}\)第\(i\)为放对或者放错
而\(v_i\)的定义就是在\(i\)位置失配后回到的长度
考虑配合\(kmp\)求出\(v\)数组
对于第\(i\)位，考虑原串内我这位是否和我\(nxt_i\)相同
如果不同，此时如果\(i\)失配，那么正好和我\(nxt_i + 1\)配上，所以$$v_i = nxt_i + 1$$
如果相同，那么失配的话我就接不到这个位置，所以不能直接转移
但是我既然相同，那么我正好接到我\(nxt_i\)的\(v\)的位置即可，所以$$v_i = v_{nxt_i}$$
但是实际处理为了第二个式子我们好转移，所以在第一个式子里我们不加那个\(1\)，最后转移的时候加就可以了
结束
AC代码
#define abhwolxq bailan
#define WWW signed
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#define M 1000005
#define ll long long
#define int long long
#define mod 1000000007
#define fre(x) freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define rep(i, a, b) for(int (i) = (a); (i) <= (b); (i)++)
#define dwn(i, a, b) for(int (i) = (a); (i) >= (b); (i)--)
using namespace std;
int wrt[20], TP;
inline int read() {int x = 0;bool f = false;char c = getchar();while(!isdigit(c)) {if (c == '-') f = true;c = getchar();}do {x = (x << 1) + (x << 3) + (c ^ 48);}while(isdigit(c = getchar()));if (f) return -x;return x;}
inline void print(int x, bool op) {TP = 0;if (x < 0) putchar('-'), x = -x;while(x >= 10) wrt[++TP] = x % 10, x /= 10;putchar(x | 48);while(TP) putchar(wrt[TP--] | 48); if (op) putchar('\n'); else putchar(' ');}
inline int qbow(int a, int b, int p) { int res = 1; while(b) { if (b & 1) res = res * a % p; a = a * a % p; b >>= 1;} return res; }
int n, nxt[M], f[M], v[M]; char c[M];
WWW main() {
scanf("%s", c + 1); n = strlen(c + 1);
int j = 0;
rep(i, 2, n) {
while(j && c[j + 1] != c[i]) j = nxt[j];
if (c[j + 1] == c[i]) j++;
nxt[i] = j;
if (i != n) {
if (c[i + 1] != c[j + 1]) v[i] = j;
else v[i] = v[j];
}
}
int inv = qbow(2, mod - 2, mod);
rep(i, 1, n) {
int len = 0;
if (c[v[i - 1] + 1] != c[i]) len = v[i - 1] + 1;
f[i] = ((f[i - 1] * 2 - f[len] - 2) % mod + mod) % mod;
}
print(mod - f[n], 0);
return 0;
}
1313
(别问我什么含义，我也不知道)
