K-means + PCA + T-SNE 实现高维数据的聚类与可视化

使用matlab完成高维数据的聚类与可视化

[idx,Centers]=kmeans(qy,3)
[COEFF,SCORE,latent] = pca(qy);
SCORE = SCORE(:,1:30);
mappedX = tsne(SCORE,'Algorithm','exact','NumDimensions',3);
c=zeros(211,3);
for i = 1 : 211
    c(i,idx(i)) = 1;
end
scatter3(mappedX(:,1),mappedX(:,2),mappedX(:,3),15,c,'fill')

%     数据qy为211个，48维。
%     K-means:  [idx,Centers]=kmeans(data,k)
%     将数据分为k类，idx为每个数据的类别标号，centers为k个中心的坐标，

%     PCA：  [COEFF SCORE latent]=princomp(X)
%     现在已经改名为pca而非princomp
%     参数说明：
%     1）COEFF 是主成分分量，即样本协方差矩阵的特征向量；
%     2）SCORE主成分，是样本X在低维空间的表示形式，即样本X在主成份分量COEFF上的投影 ，若需要降k维，则只需要取前k列主成分分量即可
%     3）latent：一个包含样本协方差矩阵特征值的向量；


% T-SNE：    mappedX = tsne(X, labels, no_dims, init_dims, perplexity)
%    tsne 是无监督降维技术，labels 选项可选；
%    X∈RN×D，N 个样本，每个样本由 D 维数据构成；
%    no_dims 的默认值为 2；（压缩后的维度） 
%    tsne 函数实现，X∈RN×D⇒RN×no_dimes（mappedX）
%    init_dims：注意，在运行 tsne 函数之前，需要使用 PCA 对数据预处理，将原始样本集的维度降低至 init_dims 维度（默认为 30）。
%    perplexity：高斯分布的perplexity，默认为 30；

 

 

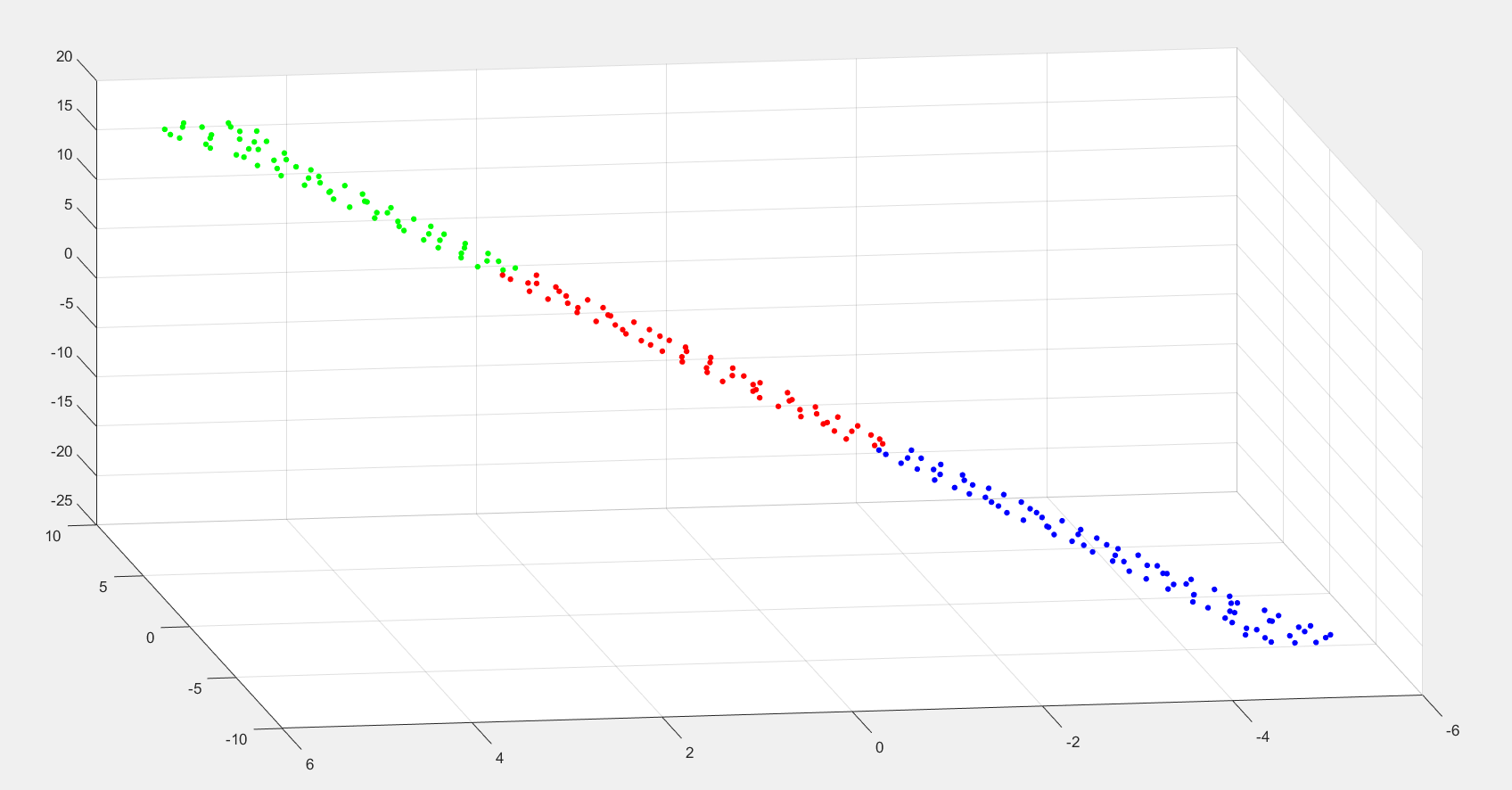
最终效果：