讲题泛做
431D Random Task
A Trick
数位 dp 答案怎么统计?用记忆化搜索的时候不用单独处理?要写好多参数啊,咋办啊,有没有不用记忆化搜索的方案啊?
当然有,从网上看到一个绝妙的统计方法可以直接统计。(例子是在网上抄的,进行了部分拓展和详解。)
比方统计数字和,拿 \(3229\) 来讲,你可以分成统计这部分的答案:\(0000-0999, 1000-1999, 2000-2999, 3000-3099, 3100-3199, 3200-3209, 3210-3219, 3220 - 3229\) 的答案。
对应到已经计算好的 dp 数组上,就是 \(f(4, 0) + f(4, 1) + f(4, 2) + 100 \times 3 + f(3, 0) + 100 \times 3 + f(3, 1) + \cdots\)(后面都是类似的)
像这样爆草数位 dp 的统计答案环节即可。
*2000,考察对题意所求值单调性的观察和证明能力,以及数位 dp 的应用
给定 \(m, k\),找到一个最小的 \(n\) 使得 \(\displaystyle\sum_{i = n + 1} ^ {2n}[\operatorname{popcount}(i) = k] = m\)。
\(m \le 10 ^ {18}, k \le 64, 1 \le ans \le 10 ^ {18}\)。
dp 好说,可是之前不是很会统计答案,因此为做一个题现场去学了数位 dp……(见上方 A Trick 部分)
考虑两个相邻的整数 \(n - 1\) 和 \(n\),发现这两个数对应需要统计 \(\operatorname{popcount}\) 的集合的不重合部分只有 \(\{n\}\) 和 \(\{2n - 1, 2n\}\),而 \(\operatorname{popcount}(n) = \operatorname{popcount}(2n)\),因此 \(\displaystyle\sum_{i = n + 1} ^ {2n}[\operatorname{popcount}(i) = k]\) 是单调不降的,二分答案即可。计算这个东西就是个比较平凡的数位 dp 了。
486D Valid Sets
*2000,考察简单树形 dp 有变化的应用。
给一棵树,点有点权,求树上有多少个子连通块满足极差不超过 \(d\)。
\(n, d, a_i\le 2 \times 10^3\)。
先考虑如何计算一棵树上的子连通块个数,考虑 dp,设 \(f(u)\) 为以 \(u\) 为根的子连通块个数:
原理也很好想,无非就是每个子节点为根的连通块要么一个都不选,要么任选一个。
另一个需要注意的问题是如何去重,发现只要限制选择连通块中的最小点权,每次统计答案的时候只统计包含最小点权的连通块,即可保证不重不漏,因此枚举最小点权,每次做一个 dp 并统计答案。
设 \(f(u, 0/1)\) 表示以 \(u\) 为根的子连通块的总个数/选中了最小点权的子连通块个数,那么 \(f(u, 0)\) 的转移同上文 \(f(u)\),\(f(u, 1)\) 可以考虑这样求得:(\(l, r\) 表示当前值域,其中 \(l\) 为最小值)
第二个转移式考虑计算每个子节点中都不包含最小点权的方案数,然后再用总方案数减去。
总的复杂度为 \(O(nw)\),其中 \(w\) 为值域,也可以通过一开始先对点权排序,只取有效点权做到 \(O(n^2)\)。
1004D Sonya and Matrix
*2300,无关键性算法,主要考察思维。
萌萌题,草可是我的实现怎么就是比大家的复杂……
给定 \(t\) 个 \(t\) 个数,问你能否用这些数构造出一个 \(n \times m\) 的矩阵,满足 \(n \times m = t\),每个数都使用一次,且在这个矩阵中能找到唯一的一个点,满足其余所有数到这个点的曼哈顿距离都等于这个数。构造一种方案,只输出 \(n, m\) 和这个点的位置即可。
先统计每个数的个数 \(c_i\)。
考虑从 \(0\) 开始一圈一圈往外加,在顶到矩阵的边界之前,一定有 \(c_i = 4i\),这里不作证明,设 \(x_1\) 为第一个满足 \(c_i < 4i\) 的 \(i\);
类似的定义 \(x_2\) 为第二次顶到边界的数,稍加分析可得 \(x_2\) 为第一个满足 \(c_i < 2(i + x_1) - 1\) 的 \(i\)。
这时取 \(x_1\) 作为零点的横坐标,\(x_2\) 作为零点的纵坐标,枚举 \(t\) 的所有因数,然后 \(O(nm) = O(t)\) bfs 推一下每个点的曼哈顿距离判断一下就行了,做到了 \(O(t\sigma_0\left(t\right))\) 的复杂度,已经可以通过。
但是这样有的时候找不到答案,比如只存在唯一解而且 \(n \ll m\) 的情况,两次顶到的边界分别是矩阵的对边,因此需要打个补丁:
考虑求出第三次顶到边界的数 \(x_3\),这里可以只考虑 \(n \ll m\) 的情况,因为哪怕求出来的不合法因为接下来会再 check 一遍因此不用担心输出不合法解。注意到一旦出现了顶到对边的情况,接下来顶到边界第三次之前一定有 \(c_i = c_{x_2}\)。因此 \(x_3\) 就是第一个满足 \(c_i < c_{x_2}\) 的 \(i\)。
p.s:根本就不用 bfs 推曼哈顿距离,可以直接枚举点然后计算曼哈顿距离,是我菜了……
762D Maximum path
*2300,思路不难但主要考验码力(?)的 dp。
给定一个 \(3 \times n\) 的棋盘每个位置上有一个权值,求从 \((1, 1)\) 走到 \((3, n)\) 的所有简单路径上的权值和的最大值。
注意到 \(3\) 很小,因此读完题就有了大致思路:
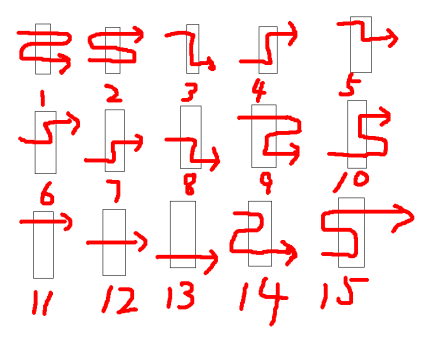
考虑按经过这三个点的顺序,分上图这十五种情况讨论(((
感觉应该是正确的,但是以有限的码力实现后可能忽略了几种状态或者转移仍旧 WA on 16(
按三个点讨论太繁琐啦!有没有什么更好的替代方案呢?
当然有,考虑每条分界线的通过状态,这样就只有五种不同情况啦:
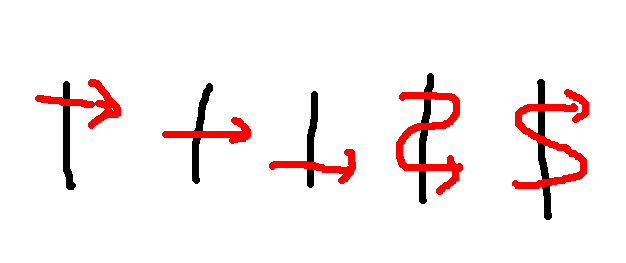
比上面那种写法好写一万倍
723F st-Spanning Tree
*2300,考察代码能力(?)。
给定一个无向图和两个点 \(s, t\) 和两个值 \(d_s, d_t\),构造一个生成树满足 \(deg(s) \le d_s, deg(t) \le d_t\)。
个人感觉思维难度偏低,最多也就 *1500 的样子,差不多读完题就能切吧(?)。
显然首先跟 \(s, t\) 都不着边的边都能一开始能加上全加上,把连成一个联通块的点缩起来之后肯定是一个这样的图:
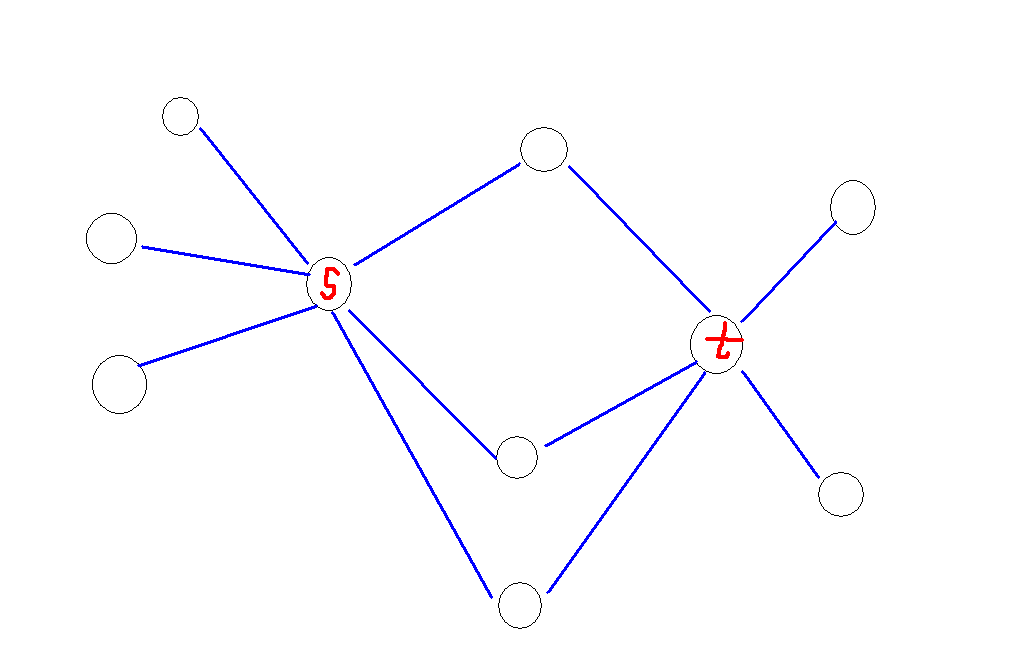
只和 \(s\) 或 \(t\) 中一个相连的点肯定得全连上,对于中间的点,把 \(s\) 或 \(t\) 其中一个的度数连满,然后再判断一下剩下的那个度数是否超过限制就行了。
可能要注意一些特殊情况比如 \((s, t) \in E\) 是割边或者图根本就不连通的情况。
这题不写了……
677D Vanya and Treasure
*2300,考察复杂度平衡及证明,代码码力。
给定一个 \(n \times m\) 的矩阵和一个参数 \(p\),每个矩阵上有一个数 \(a_{i, j} \in [1, p]\cap\mathbb Z\),要求找到一条 \(1 \sim p\) 的路径满足这条路径上所有相邻两个数的曼哈顿距离之和最短。
首先肯定得按数分层从某一层转移到下一层没的说,考虑根号分治。
- 对于出现次数 \(> \sqrt {nm}\) 的数,显然这样的数只会有 \(O(\sqrt{nm})\) 种,因此只要两层中有一层是这样的数,考虑在上一层进行多源 bfs 处理每个位置到上一个数的最短距离,复杂度显然为 \(O(nm\sqrt{nm})\)。
- 对于出现次数 \(\le \sqrt {nm}\) 的数,注意到 \(\displaystyle\sum_{c_i \le \sqrt{nm}}c_i = O(nm)\),因此直接暴力枚举相邻两层的数进行转移,考虑其中最大的 \(c_i\) 也是 \(O(\sqrt{nm})\) 的,因此即便转移发生在所有的数和出现次数最大的这个数之间,总的转移数也是 \(O(nm\sqrt{nm})\) 的。
这个题也不写了……
1342E Placing Rooks
*2300(?),考察第二类斯特林数和组合数的意义应用
在 \(n \times n\) 的棋盘上放 \(n\) 个车,
这题真的有 2300 吗……
因为只有 \(n\) 个,所以所有的格子都被占领,当且仅当每行都有或者每列都有一个车。
不妨先假设每行都有且仅有一个车。这时如果有 \(x\) 列没有车,那么就意味着有 \(x\) 个车跑到了别的车的正下方,这时这对车就能互相攻击到,可以证明这个条件是充要的。
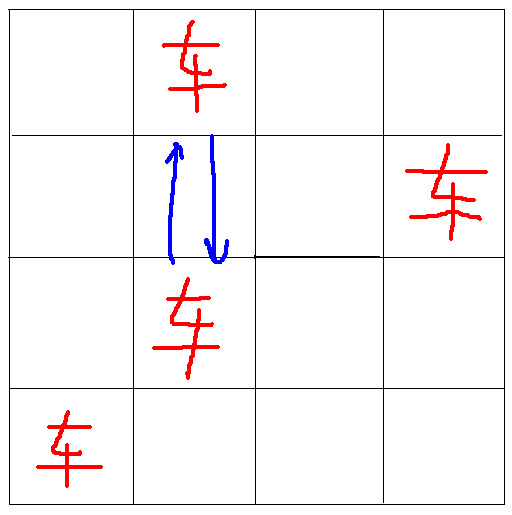
(\(x = 1\) 的情况)
因此有 \(k\) 对车互相攻击到,也就意味着有 \(k\) 列是空的,故有 \(n - k\) 列有车。
那么划分方案数就是把 \(n\) 个车划分到 \(n - k\) 个无区分集合内的方案数,然后选 \(n - k\) 列随意位置、随意顺序放置这 \(n - k\) 个集合。
故答案为 \(\displaystyle{n \brace n - k}{n \choose n - k}(n - k)!\)
uoj #246 破坏发射台
给定一个长为 \(n\) 的环,有 \(m\) 种颜色,要求相邻两个位置、相对两个位置(\(n\) 为奇数的时候视为没有相对的位置)不能同色,求染色方案数。
之前我研究过没有相对两个位置的限制时候的问题,还出过完全一致的题,是一个裸的矩阵快速幂:
考虑先固定第一种颜色,然后设 \(f(i, 0/1)\) 表示第 \(i\) 个位置与第一种颜色相同/不同的方案总数,于是有:
也可以多做一步把上面的式子代入下边做成一个广义斐波那契数列,最后的答案就是 \(mf(n, 1)\)。
有了奇数的大方向,偶数考虑在这个基础上魔改一下。
好在只是状态总数的线性增长而不是加维数,考虑同时处理位置相对的颜色对的染色方案数。
固定 \(1\) 号位置和 \(\dfrac{n}{2} + 1\) 号位置的颜色,设 \(f(i, 0/1/2, 0/1/2)\) 表示前半部分颜色与 \(1\) 号相同/与 \(\dfrac{n}{2} + 1\) 号相同/都不同,后半部分与 \(1\) 号相同/与 \(\dfrac{n}{2} + 1\) 号相同/都不同的方案数。
用与奇数完全相似的方式进行矩阵快速幂即可,就是转移麻烦了亿点点(除去不合法的 \(f(i, 0, 0)\) 和 \(f(i, 1, 1)\),还有 \(7\) 种状态,加油勇士!((()。



