【图论】网络流
文章相关
写在前面
一开始的时候,学习网络流只是因为想做 bzoj 1001。学习了 dinic 算法之后,顺便写了这么一篇学习笔记,争取能够帮到更多的同学理解网络流。
因此如果对这篇文章有什么不理解的地方,请在评论区留言,博主会尽量修改,如果能够提出改进意见,不胜感激。
概念
这些概念可能是在下文中才用得到的,因此可以先不阅读此部分。如有不理解的再回到目录部分查阅,这些概念大致按照在文章中出现的顺序排列。
网络流是图论中的一类经典问题,也是一种博大精深的问题,也是 OI 中非常有意思的一种问题。
网络
什么是网络?
可以理解为一张有向图,记这张有向图为 \(G(V, E)\)
在这张有向图的点集 \(V\) 中,有且只有一个源点 \(s\),一个汇点 \(t\) 和若干个中转点。
在边集 \(E\) 中,每条边都有一个容量 \(c\)。
这样的有向图被称为网络。
注意:网络并不是一个 DAG,也不保证 \(s\) 入度为 \(0\) 和 \(t\) 出度为 \(0\)。
流
形象的说,源点就是现实中网络上的发送站,汇点就是接收站。
发送站向接收站传输一些文件,传输的文件就是一个流。
这个流的大小称为流量 \(f\)。
显然这个流必须是从源点出发,然后经过某些中转点和边,最后到达汇点的。
这个流量不能够超过任何一条边的容量,因此若经过这些边,那么这个流的流量最大为经过的所有边的最小容量。
注意:如果一条边有 \(f\) 的流量,那么这条边的反边就有 \(-f\) 的流量。当一条边的流量增加 \(f\) 的时候,其对应的反边流量减少 \(f\)
最大流
最大流是网络流中最简单的一类问题,也是最适合新手入门的一类问题。
在网络中,类型不同的节点对流量有不同的性质,其中:
- 源点,拥有无限流量,但是不接收流量,但因为边的容量限制,真正输出的流量也有限。
- 汇点,可以无限接受流量,但是不输出流量,但因为容量限制,真正接受的流量也有限。
- 中转点,接收多少流量就输出多少流量,经过中转点既不会增加流量,也不会减少流量。
在满足所有边的容量限制的情况下,充分利用整个网络的节点,从源点出发,最后在汇点接受的最大流量,称为这个网络的最大流。
费用流
费用流的一类经典问题是“最小费用最大流”。
对于每条边,除了有容量限制之外,还有一个单位流量的花费。
“最小费用最大流”即在满足整张图取到最大流的情况下,最小化花费。
当前流
当前状态下的流被称为当前流,当前流在增广操作中会被修改,不断增广之后就会得到最大流。
可行流
一个能够到达汇点的有流量的流被称为可行流。
残余容量
对于一条边,在已经有一部分流量的基础上,剩余可用的容量被称为残余容量。
残量网络
对于整张图,在已经形成若干的流之后,由节点和所有有残余容量的边及其残余容量构成的网络被称为残量网络。
增广路
如果在网络中,能够再找到一条路径,使得整个网络依据这条路径修改当前流后能够使得整个网络的流量增加,那么这条路被称为增广路,按照增广路修改当前流的操作被称为增广。
因此,显然当前流是最大流的充要条件是在当前流下不存在任何一条增广路。
特别的,增广路在残量网络上的体现即为在残量网络上,从源点能够找到一条到达汇点的路径。
所以,当前流是最大流的充要条件等价于在残量网络上,源点和汇点不连通。
分层
一种有效给搜索节点的顺序进行排布的方式。保证只搜下一层节点可以实现在增广之后不会再影响反边。被分层处理之后的图被称为分层图。
封锁
给一个节点打上标识,使得接下来的搜索过程中无法再搜到这个节点。
割
在一个网络中,选取边集 \(E'\subseteq E\),使得断掉这些边之后 \(s\) 和 \(t\) 不连通,这样的一个边集 \(V'\) 被称为这个网络的一个割。
最小割
在一个网络中,每条边都有一个代价 \(p\),定义一个割的代价为 \(\sum_{(u, v)\in E'} p_{(u, v)}\),这个网络中代价最小的割被称为最小割。
最大流
算法
修改当前流的方法
发现若要在原图中找到一个可行流,很容易。
但是如果想要修改当前流,不是那么好实现,可能需要对当前流的某些边进行一个“反悔”。
但是,如果对于每一条初始边 \((u, v, c)\in E\),建一条反向边 \((v, u, 0)\),就可以很好的解答这个问题。
用边的权表示当前边的残余容量。
那么当在一条边上进行增广之后,这条边的流量就 \(+f\), 而反边的流量会 \(-f\)。体现为残余容量,就是正向边的残余容量 \(-f\) 而反向边的残余容量 \(+f\)。
举个例子表示一下:
图中 \(s = 1, t = 4\),蓝色数字表示容量,红色线表示当前流,红色数字表示流量。
那么此图中对应的残量网络就是:

图中绿色表示残余容量,只要有残余容量的边都标出了,包括之前的反边。
注意:在原图中形成了一个 \((1, 2, 2)\to(2, 3, 2)\to(3, 4, 2)\) 的当前流也就意味着它们边 \((2, 1),(3, 2),(4, 3)\) 的残余容量分别增加了 \(2\)。
根据在残量网络上 \(s\) 和 \(t\) 仍然连通,得出在当前流下,仍然存在增广路。
为了演示修改当前流的“反悔”过程,这里先不考虑最优性,单纯地参考当前的残量网络,按照 \((1, 3)\to(3, 2)\to(2, 4)\) 这样一条可行路径进行增广,增加的流量为 \(2\),那么,这次增广之后残量网络就变成了:

这样一次操作之后对应的当前流变成了什么样呢?这个也不难想象。
可以发现,在这样一次增广过程中,因为经过了 \((2, 3)\) 这条边的反边,所以这条边上原来形成的流就被自然的“反悔”了。
而原本的流量,没有受到任何影响,这样和直接从 \((1, 2)\to(2, 4)\) 和 \((1, 3)\to(3, 4)\) 进行增广没有任何区别。
因此,只要不断在残量网络上进行增广,就可以代替在原图修改当前流的反悔过程。
暴力算法
经过刚才的分析,我们就得到了一种非常简单且易理解的暴力算法,称为 Ford-Fulkerson 算法。
具体实现就是:
-
在残量网络上找到一条增广路。
-
对当前流进行增广。
-
重复 1, 2 过程直到 \(s, t\) 不连通为止,这时就找到了最大流。
求解最大流更高效的算法 - dinic
Ford-Fulkerson 算法易与理解,但是复杂度爆炸。我们需要更高效的算法。
简单求解网络最大流一般采用 dinic 算法。
dinic 算法的基本思想是:按照残量网络通过 bfs 对当前的节点进行分层,在得出的分层图上进行多路增广,并且及时封锁不再会对答案产生贡献的节点。
多路增广的可行性?过程中因为已经对节点进行分层,只搜索下一层的节点就不会对之前的操作产生任何影响。
多路增广和封锁无用节点是 dinic 效率高的重要原因。
实现过程:
-
通过 bfs 在残量网络上最节点进行分层,同时判断图是否连通。是,进行增广;否,直接返回,已经找到最大流。
-
通过 dfs 在分层之后的图上进行增广。每次搜索的时候强制让其只能抵达下一层的节点。如果搜到汇点,就返回当前有的流量;否则则继续往深处搜,如果回溯回来之后发现没有可行流,那么就说明在残量网络上达不到汇点,这时把这个点封锁即可。
-
重复 1, 2 过程。
扔张图理解一下,挺形象的。
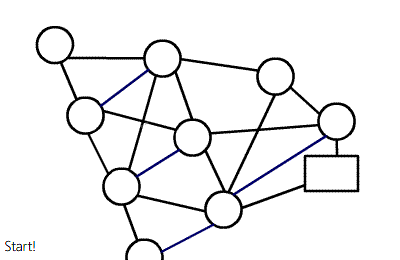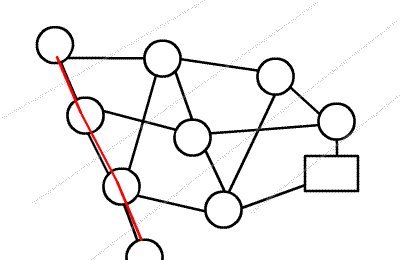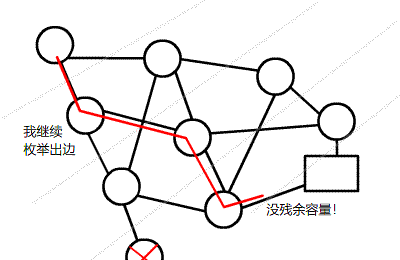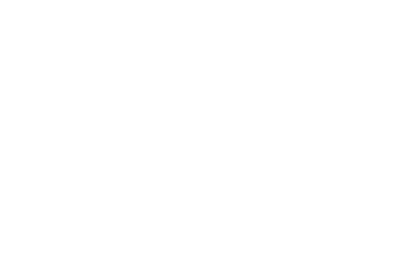
(图片来源:https://www.luogu.com.cn/blog/cicos/Dinic,侵权删)
dinic 的时间复杂度为 \(\mathcal O(n^2m)\),且大多时候跑不满,在一般处理问题中已经足够优秀。
dinic 的当前弧优化
dinic 在实际运行中的效率已经足够优秀,而且它还可以优化,这就是当前弧优化。
当前弧优化的原理是:因为 dinic 实现的是多路增广,那么可以简单理解为之前枚举过的出边都已有效增广,因此当一个点被枚举到的时候,只需要从之前枚举完的出边继续枚举就可以了。
这样,虽然渐进时间复杂度上界没有改变,但是实际上运行效率可以提升不少。
代码
定理、推论和应用
最大流 = 最小割
对于任意一个可行流 \(f\left(s, t\right)\) 的割 \(\left(S, T\right)\),我们可以得到:
如果我们求出了最大流 \(f\),那么残余网络中一定不存在 \(s\) 到 \(t\) 的増广路经,也就是 \(S\) 的出边一定是满流,\(S\) 的入边一定是零流,于是有:
(证明过程来自 OI-wiki)
二分图最大匹配
转化一下,很容易发现,一个二分图的最大匹配,就等同与分别用源点和汇点连接左右子图,然后跑最大流。
例题
最大流最小割定理:bzoj1001 [ICPC - Beijing2006] 狼抓兔子
二分图最大匹配:【网络流 24 题】飞行员配对方案
费用流
算法
ZKW 费用流
按照最短路进行分层跑的 dinic。
费用流将 bfs 改为 spfa 寻找最短路。
dijkstra 固然也是可以的,加上奇怪的处理负权边的方式就好了。




