题解：LCM

题意：

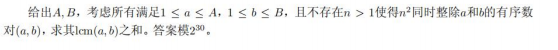
推式子

我们考虑把这个式子的形式转变一下

首先，分别整除可以转变成他们的 $gcd$ 整除

其次，考虑整除一个平方项，我们可以联想到一个欧拉函数 $\mu$

于是，我们要求的式子就变成了

$$\sum_{a=1}^A \sum_{b=1}^B [\mu(gcd(a,b))\neq 0] \frac{a*b}{gcd[a,b]}$$

很明显这里就是一个莫比乌斯反演的式子，然后按照套路把 $gcd$ 提出来

$$\sum_{\mu(k) \ neq 0 } \frac{1}{k} \sum_{a=1}^A \sum_{b=1}^B [gcd(a,b)==k] \frac{a*b}{gcd[a,b]}$$

$$\sum_{\mu(k) \ neq 0 } k \sum_{a=1}^{\frac{A}{k}} \sum_{b=1}^{\frac{A}{k}} [gcd(a,b)==k] a*b$$

然后接下来的一部分和简单数学题一样，把后面的部分进行莫比乌斯反演，然后带回来，得到

$$Ans=\sum_{\mu(k) \ neq 0 } k \sum_{d=1}^{\frac{A}{k}} \mu(d) S\Big( \Big\lfloor \frac{n}{kd} \Big\rfloor \Big)^2$$

按照套路 $T=kd$

$$Ans=\sum_{T=1}^A S\Big(\Big\lfloor \frac{A}{T} \Big\rfloor \Big)^2 \sum_{d|T \mu(k) \neq 0 } \mu \Big(\frac{T}{d}\Big) \Big(\frac{T}{d}\Big)^2 d$$

到了这一步，我们已经基本上可以做了，打一个简单的 $nlogn$ 的筛加上整除分块，复杂度就变成了 $nlogn+T\sqrt{n}$ ，常数优秀一点就可以切掉了，但是我们还有更优秀的线性筛

考虑可以把式子的后半部分表示成为

$$g(T)=\sum_{d|T} \Big(\frac{T}{d}\Big) \Big(\frac{T}{d}\Big)^2 d *f(d)$$

当$T$ 是质数的时候

$$g(T) = \mu(1) * 1 * x * f(x) + \mu(x) * x^2 * f(x)=x-x^2$$

对于不是质数的部分，我们考虑因式分解

$$x=p_1^{q_1} p_2^{q_2} ....... p_k^{q_k}$$

我们发现，当 $q_i >3$ $f(x)=0$

那么，我们假设插入一个数 $p_1$

这时候，当 $q_1>1~~ f(p_1*x)=0$

否则 ，就可以表示成为：

$$g(x*p_1)=g(p_i^2)*g(p_2^{q_2}......p_k^{q_k})$$

这两个式子一定是互质的，于是，我们就可以得到

$$g(p_1^2)=\mu(p_1)*p_1^2*p_1*f(p_1)=-p_1^3$$

然后我们就可以线性筛了

#include <bits/stdc++.h>

using namespace std;
#define re register
#define gc getchar()
inline int read() 
{
    re int x=0,f(1);re char ch=gc;
    while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=gc;}
    while(ch>='0'&&ch<='9') x=(x<<1)+(x<<3)+(ch^48),ch=gc;
    return x*f;
}
#define ll long long

const int N=4e6+10,mod=1<<30;
ll n,cn[N],pri[N],vis[N],cnt;
ll s[N],po[N];

void get(int n)
{
    s[1]=cn[1]=1;
    for(int i=2;i<=n;++i)
    {
        if (!vis[i]) po[i]=pri[++cnt]=i,s[i]=i-i*i,cn[i]=1;
        for(int j=1;j<=cnt&&i*pri[j]<=n;++j)
        {
            vis[i*pri[j]]=1;
            if(i%pri[j]==0)
            {
				cn[i*pri[j]]=cn[i]+1;
                po[i*pri[j]]=po[i];//*pri[j];
                if (cn[i]==1)
					s[i*pri[j]]=-(ll)pri[j]*pri[j]*pri[j]*s[i/po[i]];
                else s[i*pri[j]]=0;
                break;
            }
            else
            {
                s[i*pri[j]]=s[i]*s[pri[j]];
                po[i*pri[j]]=pri[j];
                cn[i*pri[j]]=1;
            }
        }
    }
    for(int i=2;i<=n;++i)
    	s[i]+=s[i-1];
}


ll ans;

inline ll S(ll x) {return x*(x+1)/2;}

int main()
{
	int T=read();
	get(N-10);
	while(T--)
	{
		ans=0;
		int a=read(),b=read();
		for(int l=1,r;l<=min(a,b);l=r+1)
		{
	    	r=min(a/(a/l),b/(b/l));
		    ans+=(1LL*S(a/l)*S(b/l)*(s[r]-s[l-1]));
		}
		cout<<(ans%mod+mod)%mod<<endl;
	}
	return 0;
}