CF 484E - Sign on Fence

E. Sign on Fence

time limit per test

4 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Bizon the Champion has recently finished painting his wood fence. The fence consists of a sequence of n panels of 1 meter width and of arbitrary height. The i-th panel's height is hi meters. The adjacent planks follow without a gap between them.

After Bizon painted the fence he decided to put a "for sale" sign on it. The sign will be drawn on a rectangular piece of paper and placed on the fence so that the sides of the sign are parallel to the fence panels and are also aligned with the edges of some panels. Bizon the Champion introduced the following constraints for the sign position:

1. The width of the sign should be exactly w meters.
2. The sign must fit into the segment of the fence from the l-th to the r-th panels, inclusive (also, it can't exceed the fence's bound in vertical direction).

The sign will be really pretty, So Bizon the Champion wants the sign's height to be as large as possible.

You are given the description of the fence and several queries for placing sign. For each query print the maximum possible height of the sign that can be placed on the corresponding segment of the fence with the given fixed width of the sign.

Input

The first line of the input contains integer n — the number of panels in the fence (1 ≤ n ≤ 105).

The second line contains n space-separated integers hi, — the heights of the panels (1 ≤ hi ≤ 109).

The third line contains an integer m — the number of the queries (1 ≤ m ≤ 105).

The next m lines contain the descriptions of the queries, each query is represented by three integers l, r and w (1 ≤ l ≤ r ≤ n,1 ≤ w ≤ r - l + 1) — the segment of the fence and the width of the sign respectively.

Output

For each query print the answer on a separate line — the maximum height of the sign that can be put in the corresponding segment of the fence with all the conditions being satisfied.

Sample test(s)

input

5
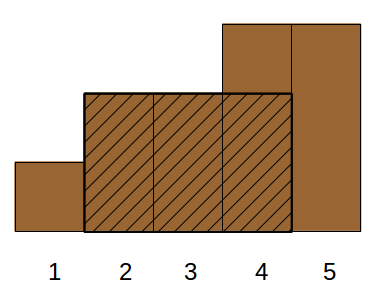
1 2 2 3 3
3
2 5 3
2 5 2
1 5 5

output

2
3
1

Note

The fence described in the sample looks as follows:

The possible positions for the signs for all queries are given below.

The optimal position of the sign for the first query.The optimal position of the sign for the second query.

 CF上的一道题，给你若干个高度不一的木板，高度为h1...hn，回答m次询问，每次询问(l,r,w)表示l...r区间内，用宽度不小于w的长条覆盖木板，长条的最大高度是多少。

CF给的题解是用函数式线段树，维护各个区间内木板高度的线段树，二分答案然后查询函数式线段树中最大的连续“1”的长度，进行比较。

可以用函数式线段树做的题，一般也可以用整体二分做。相当于一个是在线二分，一个是离线二分。

整体二分的思路是：

二分答案，把高度>mid的木板插入到线段树中，某位置有木板为1，没有为0。

对于询问，统计最大的连续“1”的长度，然后和w比较，长度>=w就往[mid+1,r]区间划分，<w就往[l,mid]区间划分。

这样二分到底层，所有询问的答案也就确定了。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <vector>
#define inf 1000000007
#define maxn 420000
#define maxm 420000

using namespace std;

int n,m,tot,cnt;
int a[maxn], ans[maxm];

struct query
{
    int id,x,y,z,cur;
    query(){}
    query(int id,int x,int y,int z,int cur):
        id(id),x(x),y(y),z(z),cur(cur){}
}q[maxm],q1[maxm],q2[maxm];

struct segtree
{
    int mx[maxn*8], lmx[maxn*8], rmx[maxn*8], size[maxn*8];
    void update(int x)
    {
        mx[x]=max(max(mx[x*2],mx[x*2+1]),rmx[x*2]+lmx[x*2+1]);
        if (lmx[x*2]==size[x*2]) lmx[x]=size[x*2]+lmx[x*2+1];
        else lmx[x]=lmx[x*2];
        if (rmx[x*2+1]==size[x*2+1]) rmx[x]=size[x*2+1]+rmx[x*2];
        else rmx[x]=rmx[x*2+1];
    }
    void build(int x,int l,int r)
    {
        if (l==r)
        {
            size[x]=1;
            return ;
        }
        int mid=(l+r)>>1;
        build(x*2,l,mid);
        build(x*2+1,mid+1,r);
        size[x]=size[x*2]+size[x*2+1];
    }
    void add(int x, int l, int r, int pos, int z)
    {
        if (l==r)
        {
            mx[x]=lmx[x]=rmx[x]=z;
            return ;
        }
        int mid=(l+r)>>1;
        if (pos<=mid) add(x*2, l, mid, pos, z);
        else add(x*2+1, mid+1, r, pos, z);
        update(x);
    }
    int ask(int x, int l, int r, int ll, int rr, int &res)
    {
        if (ll<=l && r<=rr)
        {
            int tmp=max(res+lmx[x], mx[x]);
            if (rmx[x]==size[x]) res+=size[x];
            else res=rmx[x];
            return tmp;
        }
        int mid=(l+r)>>1, tmp=0;
        if (ll<=mid) tmp=max(tmp,ask(x*2, l, mid, ll, rr, res));
        if (rr>mid) tmp=max(tmp,ask(x*2+1, mid+1, r, ll, rr, res));
        return tmp;
    }
    void init()
    {
        memset(mx,0,sizeof(mx));
        memset(lmx,0,sizeof(lmx));
        memset(rmx,0,sizeof(rmx));
    }
}tree;

void solve(int st,int ed,int l,int r)
{
    if (st>ed) return ;
    if (l>=r)
    {
        for (int i=st;i<=ed;i++) ans[q[i].id]=l;
        return ;
    }
    int mid=(l+r)>>1, n1=0, n2=0;
    for (int i=st;i<=ed;i++)
    {
        if (q[i].id==0)
        {
            if (q[i].y>mid)
            {
                tree.add(1, 1, n, q[i].x, 1);
                q2[n2++]=q[i];
            }
            else
                q1[n1++]=q[i];
        }
        else
        {
            int res=0;
            int tmp=tree.ask(1, 1, n, q[i].x, q[i].y, res);
            if (tmp>=q[i].z) 
                q2[n2++]=q[i];
            else 
                q1[n1++]=q[i];
        }
    }
    for (int i=0;i<n1;i++) q[st+i]=q1[i];
    for (int i=0;i<n2;i++) q[st+n1+i]=q2[i];
    solve(st,st+n1-1,l,mid);
    for (int i=st;i<=ed;i++)
        if (q[i].id==0 && q[i].y>mid) tree.add(1, 1, n, q[i].x, 0);
    solve(st+n1,ed,mid+1,r);
}

int main()
{
    scanf("%d",&n);
    tot=0;
    for (int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        q[tot++]=query(0,i,a[i],0,0);
    }
    scanf("%d",&m);
    int x,y,z;
    for (int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&x,&y,&z);
        q[tot++]=query(i,x,y,z,0);
    }
    tree.init();
    tree.build(1,1,n);
    solve(0,tot-1,0,inf);
    for (int i=1;i<=m;i++) printf("%d\n",ans[i]);
    return 0;
}