『STA - R3』高维立方体 题解

这题的部分分比较好拿，就不细讲了。

Subtask 3 经过简单的推导可以发现这个式子的值一定是偶数，直接输出 \(0\) 即可。

Subtask 4 求出这个式子的循环节。

Subtask 5 可以用一个大矩阵快速幂做，比较麻烦。

先考虑怎么求 \(\sum_{i=1}^{n}\operatorname{fib}^2(i)\)。如图，我们可以用若干个正方形的面积和来表示：

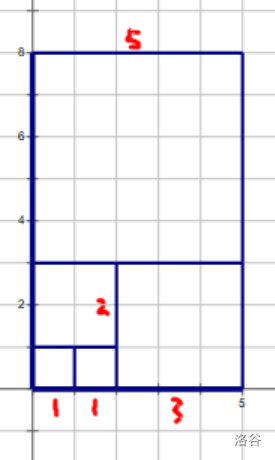
可以发现这个长方形的长是 \(\operatorname{fib}(n+1)\)，宽是 \(\operatorname{fib}(n)\)，得到：

\[\sum_{i=1}^{n}\operatorname{fib}^2(i)=\operatorname{fib}(n)\operatorname{fib}(n+1) \]

看到三个数的乘积我们可以想到立方体，上图（可能画得比较丑）：

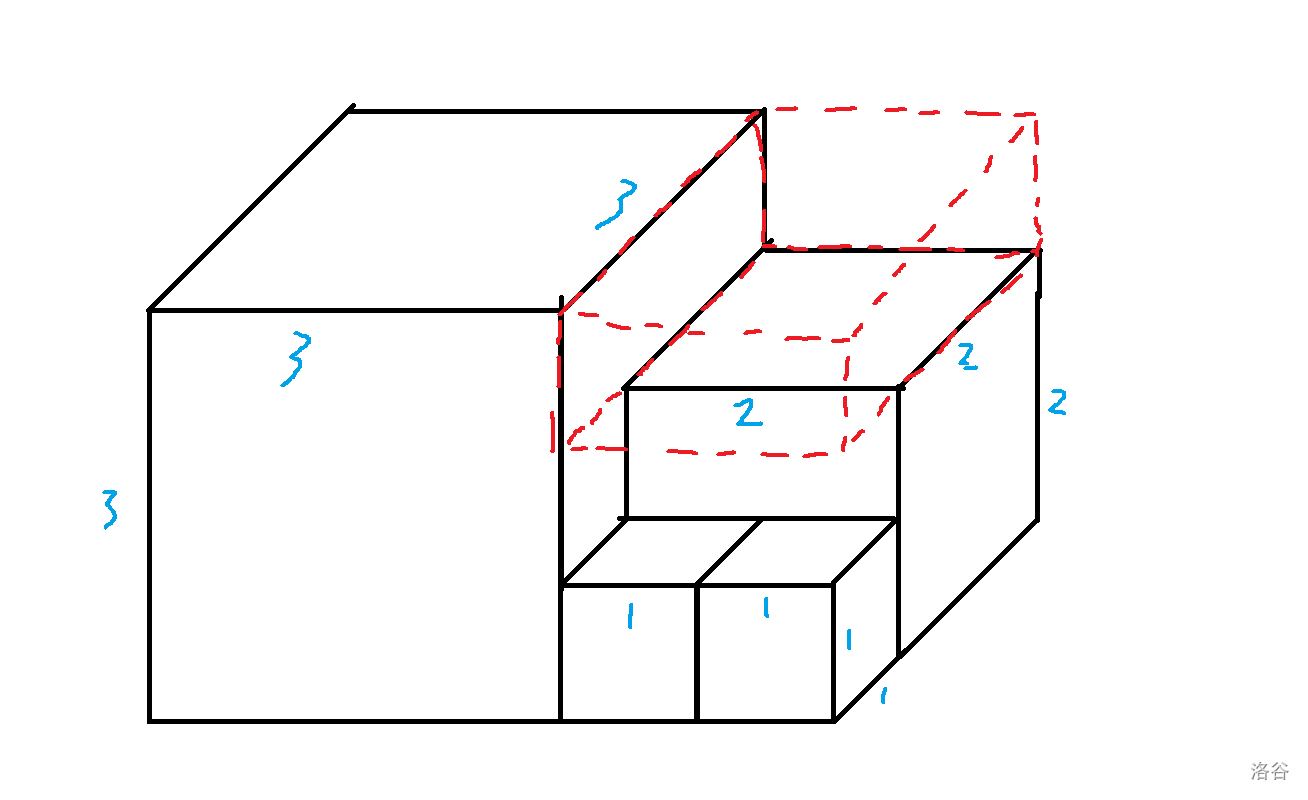
如果最大的立方体边长是 \(\operatorname{fib}(n)\)，那么红色部份的体积就是 \(\operatorname{fib}(n)\operatorname{fib}(n-1)\operatorname{fib}(n-2)\)，于是：

\[\begin{aligned} \sum_{i=1}^n\operatorname{fib}(i)\cdot(f(i-2)+\operatorname{fib}^2(i)+\operatorname{fib}(i))&= \left(\sum_{i=1}^n\operatorname{fib}(i)f(i-2)+\operatorname{fib}^3(i)\right)+\sum_{i=1}^n\operatorname{fib}^2(i)\\&= \operatorname{fib}^2(n)\operatorname{fib}(n+1)+\operatorname{fib}(n)\operatorname{fib}(n+1) \end{aligned} \]

矩阵快速幂即可，代码：

#include<bits/stdc++.h>
#define ll long long
#define rep(i,a,b) for(int i=a;i<=b;++i)
#define rept(i,a,b) for(int i=a;i<b;++i)
using namespace std;
inline ll read(){
	ll x=0;char ch=getchar();
	while(!isdigit(ch))ch=getchar();
	while(isdigit(ch))x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
	return x;
}
int t,md;
ll n,a,b,ans[3][3],l[3][3],d[3][3];
inline void mul(ll x[3][3],const ll y[3][3]){
    ll a=x[0][0],b=x[0][1],c=x[1][0],d=x[1][1];
    x[0][0]=(a*y[0][0]+b*y[1][0])%md;
    x[0][1]=(a*y[0][1]+b*y[1][1])%md;
    x[1][0]=(c*y[0][0]+d*y[1][0])%md;
    x[1][1]=(c*y[0][1]+d*y[1][1])%md;
}
inline void initd(){
	d[0][0]=0,d[0][1]=d[1][0]=d[1][1]=1;
}
void power(ll x){
    ans[0][0]=ans[1][1]=1;
    ans[0][1]=ans[1][0]=0;
    initd(); 
    for(;x;x>>=1){
        l[0][0]=d[0][0],l[0][1]=d[0][1];
        l[1][0]=d[1][0],l[1][1]=d[1][1];
        if(x&1)mul(ans,l);
        mul(d,l);
    }
}
signed main(){
	scanf("%d",&t);
	while(t--){
		n=read(),md=read();
		power(n-1);
		a=(ans[0][0]+ans[1][0])%md;
		b=(ans[0][1]+ans[1][1])%md;
		printf("%lld\n",(a*a+a)%md*b%md);
	}
	return 0;
}