[ABC286Ex] Don't Swim 题解

我们首先求出线段与多边形的交点，如果交点个数 \(<2\) 或者有无数个交点，则可以直接输出 \(S\) 到 \(T\) 之间的距离。

接下来我们考虑交点个数为 \(2\) 的情况。

为了方便，我们记距离 \(S\) 最近的那个交点为 \(P_1\)，远的为 \(P_2\)。

举个例子：

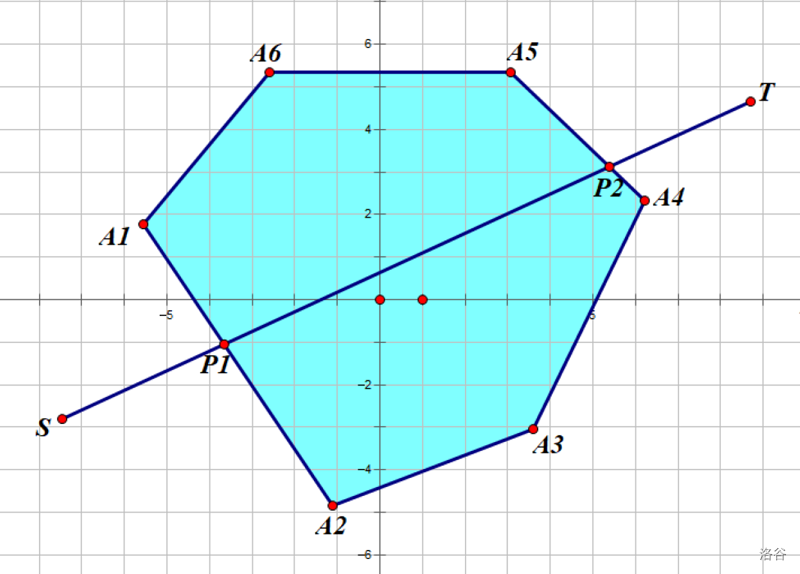
在这个例子中，直线 \(ST\) 将整个多边形分成了两个凸壳，我们可以从多边形下面过去也可以从上面过去。考虑对于两部份分别求出一条最短路径再取一个最小值。（这里上半部分指的是向量 \(\overrightarrow{ST}\) 的左半平面）

我们先考虑上半部分的一条路径 \(S\rightarrow P_1 \rightarrow A_1\rightarrow A_6 \rightarrow A_5 \rightarrow P_2 \rightarrow T\)，可以发现这条路径的一个前缀 \(S\rightarrow P_1 \rightarrow A_1\) 没有 \(S\rightarrow A_1\) 更优（三角形的性质）。

考虑按到 \(S\) 的距离的顺序枚举上半部分的所有点。我们维护一个栈，每次新加入一个点时，如果栈的大小 \(<2\)，就直接入栈。

对于其它情况，我们记当前这个点为 \(P\)，栈顶的两个点分别为 \(A,B\)（\(A\) 比 \(B\) 先入栈），考虑向量 \(\overrightarrow{AB}\) 与向量 \(\overrightarrow{BP}\) 的叉积，如果符号不为负则将 \(B\) 弹出栈，重复这个操作直到符号不为负或者栈的大小 \(<2\)。最后再将 \(P\) 入栈。

那么路径的长度就是最后的栈中相邻两个点的距离的和。对于下半部分也是类似的操作，但是在判断叉积的符号时如果符号不为正才将 \(B\) 弹出栈。

那么剩下的问题就是如何求出两半部份的点了。我们记 \(P_1\) 所在的线段的两个端点分别是 \(A_i,A_{(i+1)\mod n}\)（如果存在多条线段则任取一个），\(P_2\) 所在的线段的两个端点分别是 \(A_j,A_{(j+1)\mod n}\)，那么点 \(A_{i+1},A_{i+2},\dots,A_{n-1},A_0,A_1,\dots A_j\) 属于下半部分，剩下的就属于上半部分。

代码：

#include<bits/stdc++.h>
#define ll long long
#define mxn 100003
#define md 1000000007
#define pb push_back
#define mkp make_pair
#define ld long double
#define umap unordered_map
#define rep(i,a,b) for(int i=a;i<=b;++i)
#define rept(i,a,b) for(int i=a;i<b;++i)
#define drep(i,a,b) for(int i=a;i>=b;--i)
#define pq priority_queue
using namespace std;
struct point{
	ld x,y;
	inline void in(){
		scanf("%Lf%Lf",&x,&y);
	}
}s,t,a[mxn],q[mxn+10];
struct line{
	ld k,b;
	line(point x,point y){
		k=(y.y-x.y)/(y.x-x.x);
		b=x.y-x.x*k;
	}
	inline ld at(ld x){
		return x*k+b;
	}
};
const ld esp=1e-8;
inline point operator-(point x,point y){
	return {x.x-y.x,x.y-y.y};
}
inline bool operator==(point x,point y){
	return fabs(x.x-y.x)<esp&&fabs(x.y-y.y)<esp;
}
inline bool operator==(line x,line y){
	return fabs(x.k-y.k)<esp&&fabs(x.b-y.b)<esp;
}
inline point operator&(line a,line b){
	ld x=(b.b-a.b)/(a.k-b.k);
	return {x,a.k*x+a.b};
}
inline ld operator*(point x,point y){
	return x.x*y.y-x.y*y.x;
}
inline int cmp(ld x){
	if(fabs(x)<esp)return 0;
	return x<0?-1:1;
}
inline ld len(point x){
	return sqrt(x.x*x.x+x.y*x.y);
}
int n,m;
vector<pair<point,int> >st,d1;
ld ans1,ans2;
inline void add1(point x){
	while(m>1&&(x==q[m]||cmp((q[m]-q[m-1])*(x-q[m]))!=1))m--;
	q[++m]=x;
}
inline void add2(point x){
	while(m>1&&(x==q[m]||cmp((q[m]-q[m-1])*(x-q[m]))!=-1))m--;
	q[++m]=x;
}
signed main(){
	scanf("%d",&n);
	rept(i,0,n)a[i].in();
	s.in(),t.in();
	line d(s,t);
	rept(i,0,n){
		line x(a[i],a[(i+1)%n]);
		if(s.x==t.x&&a[i].x==a[(i+1)%n].x){
			if(s.x==a[i].x){
				printf("%.10Lf",len(s-t));
				return 0;
			}
			continue;
		}
		if(s.x!=t.x&&x.k==d.k){
			if(x.b==d.b){
				printf("%.10Lf",len(s-t));
				return 0;
			}
			continue;
		}
		point p;
		if(s.x==t.x){
			p={s.x,x.at(s.x)};
		}else if(a[i].x==a[(i+1)%n].x){
			p={a[i].x,d.at(a[i].x)};
		}else p=x&d;
		if(p.x>=min(a[i].x,a[(i+1)%n].x)&&p.x<=max(a[i].x,a[(i+1)%n].x)&&p.x>=min(s.x,t.x)&&p.x<=max(s.x,t.x)&&p.y>=min(a[i].y,a[(i+1)%n].y)&&p.y<=max(a[i].y,a[(i+1)%n].y)&&p.y>=min(s.y,t.y)&&p.y<=max(s.y,t.y)){
			d1.pb(mkp(p,i));
		}
	}
	for(auto i:d1){
		for(auto j:st)if(i.first==j.first)goto next;
		st.pb(i);
		next:;
	}
	if(st.size()!=2){
		printf("%.10Lf",len(s-t));
		return 0;
	}
	if(len(s-st[0].first)>len(s-st[1].first))swap(st[0],st[1]);
	add1(s),add1(st[0].first);
	int i=(st[0].second+1)%n;
	while(1){
		add1(a[i]);
		if(i==st[1].second)break;
		i=(i+1)%n;
	}
	add1(st[1].first),add1(t);
	rep(i,2,m)ans1+=len(q[i]-q[i-1]);
	m=0;
	add2(s),add2(st[0].first);
	i=st[0].second;
	while(1){
		add2(a[i]);
		if(i==(st[1].second+1)%n)break;
		i=(i+n-1)%n;
	}
	add2(st[1].first),add2(t);
	rep(i,2,m)ans2+=len(q[i]-q[i-1]);
	printf("%.10Lf",min(ans1,ans2));
	return 0;
}