优化算法
一、总概
优化算法主要分为两大阵营:梯度下降学派和牛顿法学派。

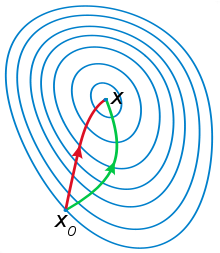
这两者的区别[1]:比如你想找一条最短的路径走到一个盆地的最底部,梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步,牛顿法在选择方向时,不仅会考虑坡度是否够大,还会考虑你走了一步之后,坡度是否会变得更大。所以,可以说牛顿法比梯度下降法看得更远一点,能更快地走到最底部。也就是说梯度下降法只考虑了一阶,而牛顿法则考虑了二阶。
二、梯度下降法
1. 最速梯度下降法和梯度下降法区别及联系[3]
1.1 原理
最速梯度下降法解决的问题是无约束优化问题,而所谓的无约束优化问题就是对目标函数的求解,没有任何的约束限制的优化问题。
最速梯度下降法的求解步骤如下:

由以上计算步骤可知,最速下降法迭代终止时,求得的是目标函数驻点的一个近似点。其中确定最优步长 的方法如下:

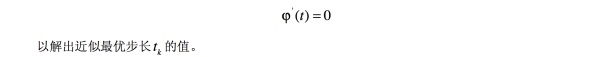
1.2 优势
1.2.1 在优化初始阶段,目标函数下降较快。
1.3 劣势
1.3.1 在接近极值点时,收敛速度较慢。因此在实用中常用最速下降法和其他方法联合应用,在前期使用最速下降法,而在接近极小值点时,可改用收敛较快的其他方法。
1.4 区别
最速梯度下降法和梯度下降法最大的区别就是:步长(学习率)。梯度下降法的α是预先设定好,而最速梯度下降法的步长是自己学习得到。

2.梯度下降法(GD)、随机梯度下降法(SGD)以及小批量梯度下降法(MBGD)区别及联系
2.1 GD
GD(Gradient Descent)是最常用的方法之一,原理:在整个训练集中计算当前的梯度,选定一个步长进行更新。
优点:
a) 基于整个数据集,梯度更加准确,更新更准确。
缺点:
a) 当训练集较大时,GD梯度计算较为耗时。
b) DL的网络loss function往往非凸,最终收敛点很容易落在初始点附近的local minima,不太容易达到较好收敛性能。
2.2 SGD
SGD(Stochastic Gradient Descent)与GD的差异是每次只计算一个样本。
优点:
a) 计算快
b) 适合online-learning 数据流式到达的场景。
缺点:
a) 单个sample产生梯度往往很不准,所以得用很小的学习率。
b) cpu/gpu 支持多线程,单个很难占满使用,浪费资源。
2.3 MBGD
MBGD(Mini-Batch Gradient Descent) 是介于两者之间的一种折中做法,一次采用batch_size的样本来计算梯度,比SGD准且充分利用资源,而且能有适当的梯度噪音,一定程度缓解GD直接进入初始点附近local minima导致收敛不好问题,所以最为常用。
mini-batch 过程中,一个epoch会分多个batch,每个batch随机抽样一批数据,更新参数,直至所有的数都被遍历一遍,一次epoch结束。batch_size为一个batch中含有样本的数量,nb_epoch为epoch次数。
2.4 备注
补充一个这三者区别解释很好的博客[4]:http://www.cnblogs.com/maybe2030/p/5089753.html
三、
四、
五、参考文献
[1]. https://zhuanlan.zhihu.com/p/22461594
[2].https://www.zhihu.com/question/32675289
[3].https://zhuanlan.zhihu.com/p/32709034
[4].http://www.cnblogs.com/maybe2030/p/5089753.html


