L2R 一：基础知识介绍

一、背景

　　l2r可以说是搜索推荐里面很常用的知识了，一直处于一知半解的地步，今天开个博客准备把这些零散的东西系统性整理好，一版就粗糙点了。

 

二、粗概

　　前段时间的项目主要和搜索引擎相关，记录下搜索引擎的主题思路，大致就是：召回 --> 粗排 ---> 精排。

　　一般情况下，召回和粗排会并在一起，例如LUCENE。召回的方法有很多种，常见的有：BM25，TF-IDF等，但不限于这些，用LDA也未尝不可。因为这一阶段是海选，涉及大量数据计算，为了保证时效，这部分的算法一般会选用快捷有效且相对简单的，重头戏都会放在精排阶段，也就是我们要说的L2R(Learning to Rank)。

　　

　　L2R按照方法类型，主要分为以下三种：pointwise, pairwise以及listwise。具体算法以及相应的类型，可参见wiki中的标记[1]。pointwise更适用于ordinal regression，而后两者更适用于L2R[2]。

 

三、基本知识

　　1. bagging 、boosting及stacking 区别[3][8]

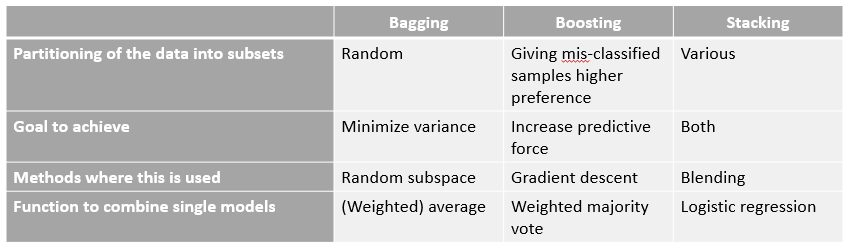
　　　　1.1 bagging方法也称为自举汇聚法（bootstrap aggregating，bootstraps:名字来自成语“pull up by your own bootstraps”，意思是依靠你自己的资源，它是一种有放回的抽样方法），是在原始数据集中选择S次后（有放回）得到S个新数据集的一种技术，新数据集和原数据集的大小相等，新数据集中可以有重复值出现，也有可能原始数据集中的某些值在新数据集中不会出现。然后利用S个新数据集，将某个学习算法分别作用于每个数据集就得到了S个分类器，最终将这S个分类器ensemble起来就得到最终的结果。算法如：随机森林（random forest）。

　　　　1.2 boosting是一种与bagging类似的技术，两者所使用的多个分类器的类型都是一致的，主要的区别就是，boosting的分类器之间是串行训练获得的，每个新分类器都是根据已训练出的分类器的性能来训练，通过几种关注被错分的数据来获得新的分类器。boosting分类的结果是基于所有分类器的加权求和的结果，所以它中分类器的权重并不相等，每个权重代表的是其对应分类器在上一轮迭代中的成功度，而bagging中，每个分类器的权重是相等的。算法如：Adaboost(adaptive boosting).

　　　　1.3 stacking是一种meta_calssifier，分两步，第一步的做法类似于bagging，首先训练集再划分出两部分（子训练集+子测试集），然后是常用的做法，得到一个弱模型，求得这个弱模型在子预测集及预测集上的预测结果（这个很重要，作为第二步的输入）。利用cross_validation，迭代几次，将每个子集作为测试集得到一遍测试结果，这个作为新训练集的X，Y保持不变。再利用每个弱模型预测测试集的结果，平均后作为新测试集的X，Y保持不变。第二步，更新训练集和测试集的X，重新学习一个分类器。[6]以上就是stacking的第一层，在第二层中，我们以第一层的输出train再结合其他的特征集再做一层stacking。不同的层数之间有各种交互，还有将经过不同的 Preprocessing 和不同的 Feature Engineering 的数据用 Ensemble 组合起来的做法。 

 　　 [7]

 

 

　　2. 分类树和回归树

　　决策树主要分为两类：分类树和回归树。

　　　　2.1 分类树常用来解决分类问题，比如用户性别、网页是否是垃圾页面、用户是不是作弊等。

　　　　2.2 而回归树一般用来预测真实数值，比如用户的年龄、用户点击的概率、网页相关程度等等。

　　　　2.3 回归树总体流程类似于分类树，区别在于，回归树的每一个节点都会得到一个预测值，以年龄为例，该预测值等于属于这个节点的所有人年龄的平均值。分枝时穷举每一个feature的每个阈值寻找最优切分变量和最优切分点，但衡量的准则不再是分类树中的基尼系数，而是平方误差最小化。也就是被预测错误的人数越多，平方误差就越大，通过最小化平方误差找到最可靠的分枝依据。分枝直到每个叶子节点上人的年龄都唯一或者达到预设的终止条件(如叶子个数上限)，若最终叶子节点上人的年龄不唯一，则以该节点上所有人的平均年龄做为该叶子节点的预测年龄。

 

　　3. bias 和variance

　　　　

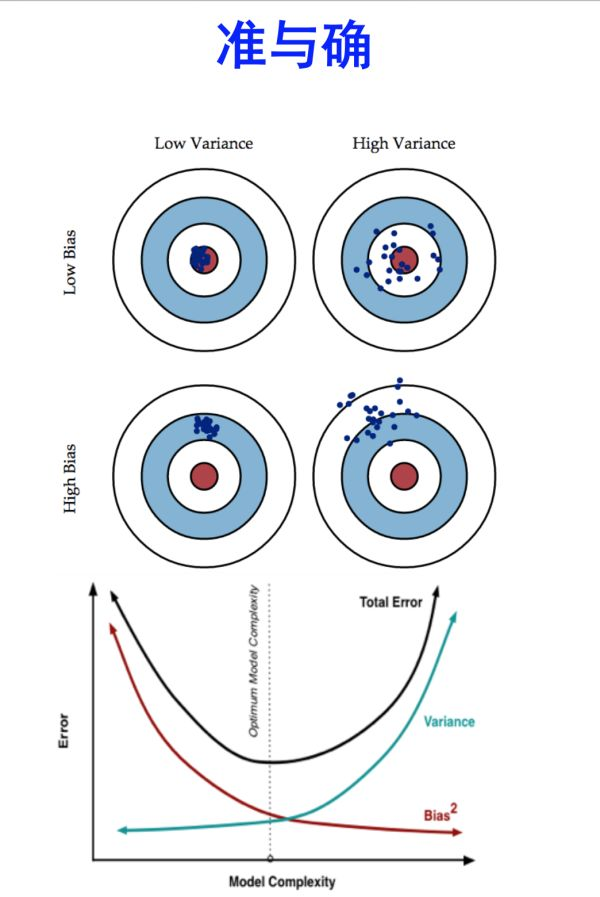
　　　　链接中说明，bias 相当于模型训练的评价指标，variance则表示了模型的泛化能力[4]。

　　　　3.1 bagging 减少 variance, boosting 减少bias，bagging对样本进行不断重新采样和聚合，减少了单个样本对于模型的影响，增加了模型本身的抗干扰能力，所以降低了variance。而boosting是串行叠加训练，不断增加每个样本的影响，对样本的依赖也比较大，这样虽然能很好的拟合训练集，bias就降低了，但是当训练集出现问题时，模型的波动也会比较大，高variance。　　　　

 

四、评价指标

　　1. NDCG[5]

 

 

 

 

五、参考文献

　　1.https://en.wikipedia.org/wiki/Learning_to_rank

　　2.Hang Li, Learning to Rank, ACML 2009Tutorial.

　　3.机器学习实战[M].第七章，利用AdaBoost元算法提高分类性能。

　　4.https://zhuanlan.zhihu.com/p/28769940   https://www.zhihu.com/question/27068705/answer/137487142 http://scott.fortmann-roe.com/docs/BiasVariance.html

　　5.https://en.wikipedia.org/wiki/Discounted_cumulative_gain

　　6.https://blog.csdn.net/Mr_tyting/article/details/72957853

　　7.https://stats.stackexchange.com/questions/18891/bagging-boosting-and-stacking-in-machine-learning

　　8. Comparison of Bagging, Boosting and Stacking Ensembles Applied to Real Estate Appraisal