机器学习-----笔记
花了2个星期看完了《机器学习实战》这本书,感觉好像入门算法了,特此做个看书总结。
本书大致包括3个部分:
第一部分:监督学习:分类+利用回归预测数值型数据
这部分包括分类算法:k-近邻算法,决策树,朴素贝叶斯,Logistic回归,支持向量机,AdaBoost元算法;回归算法:树回归;
1.k-近邻分类算法
概述:采用测量不同特征值之间的距离方法进行分类。
工作原理:现在有一个样本数据集合,其中每个数据都存在标签,换言之,我们知道数据集中每一数据于所属分类的对应关系。
之后输入没有标签的新数据后,将新数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本集中特征最相似数据(最近邻)的分类标签。
(注:一般只取数据集中前k个最相似的数据)
2.决策树
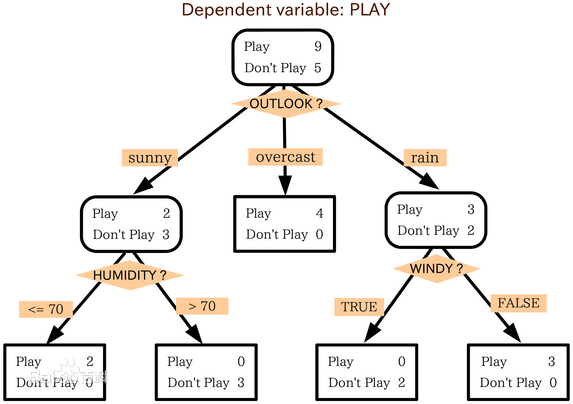
概念:如上图所示,上图是一个根据天气情况来决定是否出去玩的人数的决策树,决策树的任务就是为了数据中所蕴含的知识信息,我们从决策树中提取出一系列规则,这就是机器学习的过程。
3.朴素贝叶斯
本节介绍了基于概率论的分类器,之所以称之为‘朴素’,是因为整个形式化过程只做最原始、最简单的假设;

看上图,首先我们设p1(x,y)表示数据点(x,y)属于类别1(图中圆点表示的类别)的概率,p2(x,y)表示数据点(x,y)属于类别2(图中三角形表示的类别)的概率,
现在有2种情况:
① p1(x,y)>p2(x,y) 那么类别为1
②p1(x,y)<p2(x,y) 那么类别为2
最终我们会选择高概率对应的类别,这就是贝叶斯理论的核心思想。
4.Logistic回归
本节介绍了Logisitc回归,它的思想是根据现有的数据对分类边界线建立回归公式,以此来分类。
这里的‘回归’意思是最佳拟合,换言之,就是要找到最佳拟合参数集。
5.支持向量机(SVM)
SVM支持向量机是一种分类器,之所以称之为‘机’是因为它会产生一个二值决策的结果,即它是一种决策机,支持向量机的泛化错误率较低,具有良好的学习能力和推广性,是监督学习中最好的定式算法。
SVM尝试通过求解一个二次优化问题来最大化分类间隔。
6.AdaBoost元算法
本节介绍了2种集成方法是bagging和boosting,其中介绍了boosting方法中较为流行的算法-----AdaBoost算法,AdaBoost算法以弱学习器作为基分类器,输入数据,使其通过权重向量进行加权,在第一次迭代中,所有数据都等权重,
但在后续的迭代中,前次迭代中分错的数据权重会增大,这种针对错误的调节能力正是AdaBoost的长处。
7.回归
回归与分类一样,也是预测目标值的过程,回归与分类的不同点在于,前者是预测连续型变量,而后者是预测离散型变量;
我们可以利用回归方程,求得特征对应的最佳回归系数-----最小化误差的平方和;
接下来介绍树节点,对于具有复杂相互关系的数据集,一般采用树结构来对这种数据建模,若叶节点使用的模型是分段常数则称为回归树,若叶节点使用的模型是线性回归方程则称为模型树,同时介绍一种算法-----CART算法,它可以
用于构建二元树,并处理离散型或连续型数据的切分,CRAT算法构建出的数会倾向于对数据过拟合,为了解决这个问题,我们需要采用剪枝技术------预剪枝(在树的构建过程中就进行剪枝)和后剪枝。
第二部分:无监督学习
这部分包括:K-均值聚类算法,Apriori算法,FP-growth算法
1.K-均值聚类算法
k是用户指定的要创建的簇的数目,该算法以k个随机质心开始,计算每个点到质心的距离,每个点会被分配到距其最近的簇质心,然后紧接着基于新分配到簇的点更新簇质心,然后重复数次以上过程,
直到簇质心不再改变;该算法简单,但是容易受到初始簇质心的影响,为了获得更好的聚类效果,它的一种优化算法-----二分K均值聚类算法,该算法首先将所有点作为一个簇,然后使用k均值算法对其划分,下一次迭代时,选择有最大误差的簇进行划分,重复该过程直到k个簇创建成功为止;
2.Apriori算法
该算法主要用于关联分析,换言之,就是发现大数据集之间的关系,通常来说,我们从两个方面入手,第一种方式是使用频繁项集,它会给出经常一起出现的元素项,第二种方式就是发现关联规则;
而该算法就是采取第一中发现来进行关联分析,Apriori算法原理是说如果一个元素项是不频繁的,那么那些包含该元素的超集也是不频繁的;所以该算法从单元素项集开始,通过组合满足最小支持度的项集来形成更大的集合;
3.FP-growth算法
同上一个算法,FP-growth算法也是用于发现数据集中频繁项集,在该算法中,数据集存储在一个称为FP数的结构中,FP数构建完成后,可以通过查找元素项的条件基及构建条件FP数来发现频繁项集,本过程可以不断以更多元素作为条件重复进行,知道FP数只包含一个元素为止;
第三部分:其他工具
这部分包括:PCA(主成分分析),SVD(奇异值分解),MapReduce(规约)
1.主成分分析(PCA)
主要采取的是降维技术,目标是去除数据中的噪声,PCA可以从数据中识别其主要特征,它是通过沿着数据最大方差方向旋转坐标轴来实现的,选择方差最大的方向作为第一条坐标轴,后续坐标轴则与前面的坐标轴正交。协方差矩阵上的特征值分析可以用一系列的正交坐标轴来获取。
2.奇异值分解(SVD)
SVD也是采取降维技术,我们可以利用SVD来逼近矩阵并从中提取重要特征,还有就是SVD在推荐引擎上应用较多,其中的核心技术是协同过滤,也是一种相似度计算方法,可以用于计算物品或者用户之间的相似度,SVD通过在低维空间下计算相似度,SVD可以提高推荐系统的效果。
3.规约(MapReduce)
Map阶段并行处理数据,之后这些数据在Reduce阶段合并;(两个阶段采取的是key/value键值对形式)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号