B-Spline

B-Spline

注：
本文只是作者自己对B样条的理解和实现，如有错误欢迎指出，谢谢。
作者邮箱：zhywyt@hdu.edu.cn
B-Spline 是图形学中非常基础的一个曲线，我的导师徐岗徐老师，让我们从 B样条的绘制开始，无疑是一个很好的开始。

同 Bezier 曲线，B样条也是一个由伯恩斯坦基函数加权得到的曲线，因此它和 Bezier 曲线有这很多的相似点，这里我们把 Bezier 曲线和 B 样条放在一起来研究。

贝塞尔曲线：

\[\vec{P(t)}=\sum_{i=0}^{n-1}\vec{p_i}B_{i,n}(t),t \in [0, 1] \]

B 样条曲线：

\[\vec{P(t)}=\sum_{i=0}^{n-1}\vec{p_i}B_{i,d}(t)，其中 t_{min}\leq t \leq t_{max}，2\leq d \leq n \]

可以看到两个曲线的区别就在于基函数的定义：Bezier 曲线的基函数只与曲线的控制点数有关，曲线的控制点数就确定了曲线的阶数；而 B 样条的基函数中，n 换成了 d ，这也意味着曲线的控制点数不再决定曲线的阶数，而是独立的一个自由度。

下面是我的一些符号规定：

\[\begin{array} {cll} \hline 参数名 & 符号 \\ \hline 参数 & t\\ 顶点数 & n+1 \\ 曲线阶数 & p \ \&\ d \\ 控制顶点 & P_i \\ 下标为\ i \ 的节点向量 & u_i \\ 基函数的次数 & p-1\\ 第\ i+1\ 个控制顶点的\ j\ 阶基函数 & B(i,j)\\ 头节点重数 & h \\ 节点向量个数 & n+p \\ 自由度 & n,p,h\\ \hline \end{array} \]

解释：曲线阶数在数学中我一般使用\(d\)，而在代码中我喜欢使用\(p\)

为什么要修改基函数？

众所周知，Bezier 曲线的一大缺陷就是曲线的定义是全局的，移动一个控制点就会影响整条曲线，但是设计上往往希望能够局部修改。于是产生了分段 Bezier 曲线，但是新的问题出现了：分段 Bezier 曲线的连续性很难保证，不能达到很好的效果。B 样条因此诞生，以修改基函数的方式达到目的。

为什么修改基函数可以达到这个效果？

B 样条曲线：

\[\vec{P(t)}=\sum_{i=0}^{n-1}\vec{p_i}B_{i,d}(t)，其中 t_{min}\leq t \leq t_{max}，2\leq d \leq n \]

再来理解一下曲线的定义，每个控制点，在参数 t 处的对曲线影响的权值由基函数控制。要控制每个点的影响范围，就需要定义基函数的非零区间，在非零区间里，该控制点就对曲线有影响，而在零区间，就没有任何影响。这样的话，就能控制每个点对曲线影响的范围了。
在此之前，先介绍一下节点向量的概念。

B样条的节点向量

节点向量描述了B样条曲线上某一参数 t对应基函数的哪一部分。你可以把它想象成一部电影的时间线，给定一个时间就能得到相应的画面，而B样条就是给定一个参数 t就能得到对应的坐标。
下面是一个例子：

• \(P_i:\) 第 i 个控制点
• \(u_i:\) 下标为 i 的节点向量的值
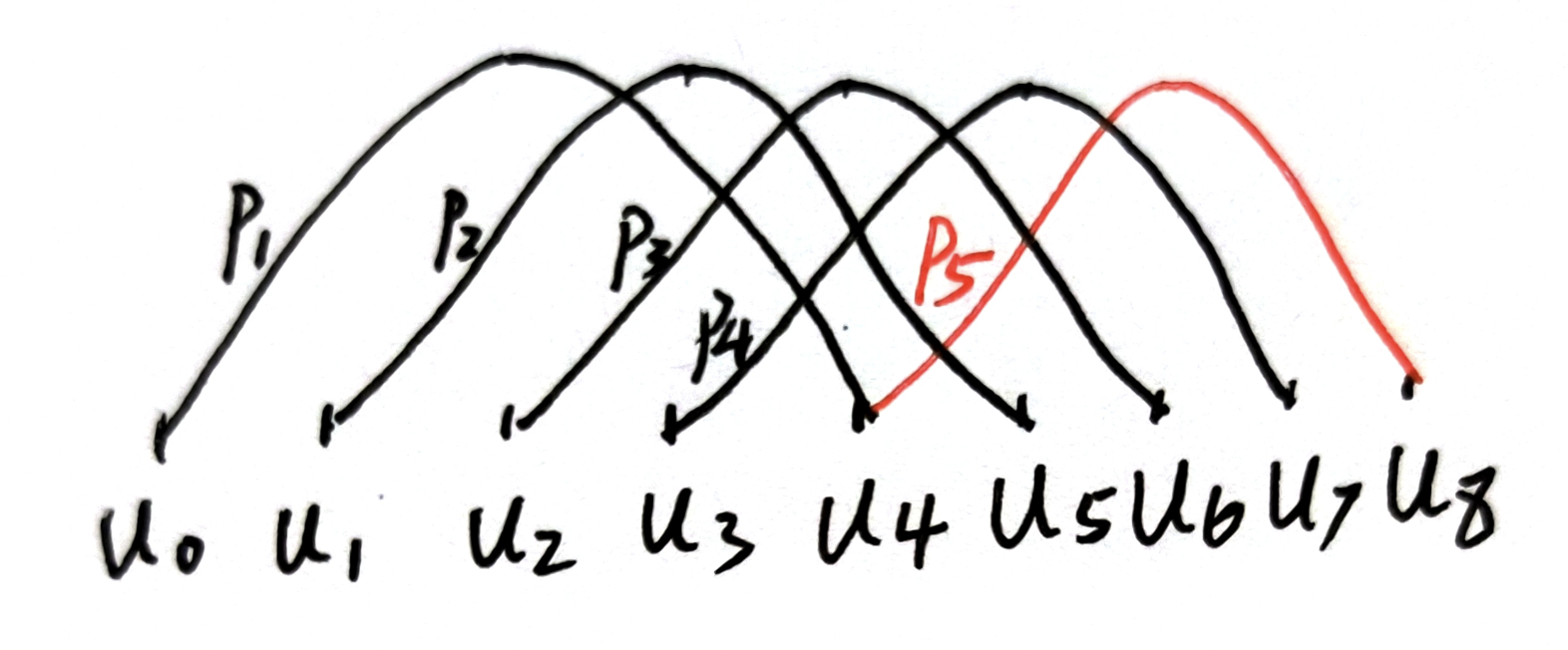
  下图是一个有五个控制顶点的(\(n+1=5\))，四阶B样条(\(p=4\))。\([u_0 , u_8]\)就是节点向量了，而上面画的曲线则是某个控制点对下面的区间的参数的权值。给定一个节点向量，就能唯一确定一个基函数的对应关系，比如最简单的，\(u_0\)对应参数的点，只被\(P_1\)这个点所影响，而\(u_3\)却被\(P_1，P_2，P_3，P_4\)四个点所影响。当然，你会发现区间\([u_0 , u_3]\)其实是被小于曲线阶数的顶点所影响的，它的权值和不等于一，这不满足B样条曲线的性质，实际上B样条的定义不从\(u_0\)开始，\(u_0\)的存在仅仅是为了其他区间的计算权值。这也就反映了B样条参数的定义域了。不是\([0,1]\)而是根据节点向量的\([u_{p-1},u_{n+1}]\)在下面这个例子中是区间\([u_3 , u_5]\)。
  
  可以很清楚的看到，\(P_1\)控制点不会影响到\(u_5\)及以后的曲线。每一段曲线比如\([u_3, u_4]\)只由\(P_1 - P_4\)四个控制点所影响，实现了曲线的局部控制。

这样的基函数如何定义？

从一个简单的一阶基函数定义看起：

\[B_{k,1}(u) \begin{cases} 1 , u[k]\leq u\leq u[k+1]\\ 0 , else \end{cases} \]

它只有在自己的定义区间内才有值 1，其余部分都为 0。
画出来也非常的清晰：

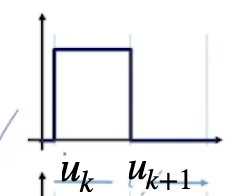
那么如果要进行升阶，我们就需要使用两个定义在相邻区间的一阶基函数：

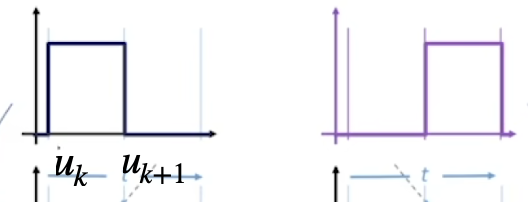
通过一个简单的线性组合就能得到二阶的基函数：

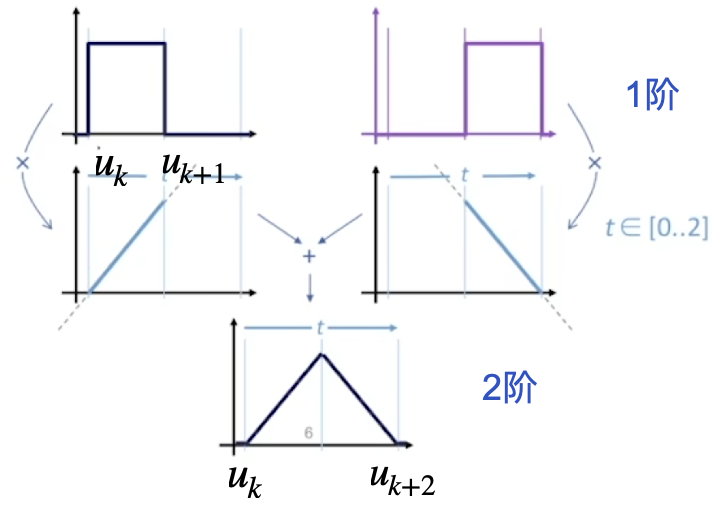
可以看到这个基函数的定义域成为了两个低阶基函数定义域的并集，从定义上看这个线性组合就是：

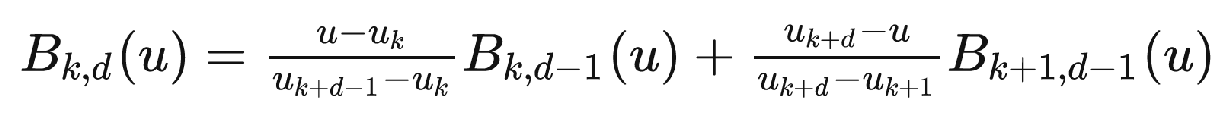
先不要害怕两个奇怪的权值，观察上面的一阶到二阶的加权不难发现，这两个权值其实是曲线在参数为 u 处的简单加权。也就是上面出现过的一次加权直线的函数取值。但是你可能会觉得奇怪，当\(u\leq u_{k+1}\)的时候，第二项的权值好像大于一了？！这不对吧？

实际上在\(u\leq u_{k+1}\)的时候，右边这一项\(B_{k+1,d-1}(u)\)的值等于零了。

看下面这个图，计算三阶基函数会显得更清晰：

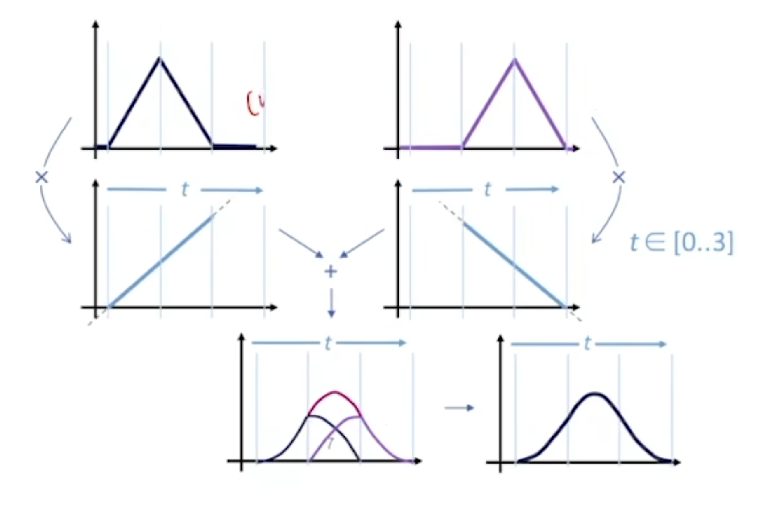
于是我们得到完整的 B 样条数学定义：

\[\begin{cases} \begin{cases} 1 , u_k \leq u\leq u_{k+1}\\ 0 , else \end{cases} \quad ,k = 1 \\ B_{k,d}(u)=\frac{u-u_k}{u_{k+d-1}-u_k}B_{k,d-1}(u)+\frac{u_{k+d}-u}{u_{k+d}-u_{k+1}}B_{k+1,d-1}(u) \quad ,k \ge 2 \end{cases} \]

B样条的自由度

说到 B 样条，就不得不说说它的自由度了。相比于 Bezier 曲线仅有的一个自由度（顶点数），均匀B 样条的自由度可多达三个（个人理解）：顶点数、曲线阶数、头节点重数设置（非均匀B样条修改为节点向量的设置即可）。姑且允许我这么随便的称呼自由度，可能不是那么标准，但是我是想让你明白 B 样条需要设置哪些参数。这里，我们讨论的是（准）均匀节点的 B 样条，也就是节点向量只会在头和尾相等而在中间以相同速率增加。比如：

n+1	: 5			number of control points.
p	: 4			rank of BSpline.
h	: 1			repeat of head and tail.
nv	: 9			number of node vector.
head vector:
0 0.111111 0.222222 0.333333 0.444444 0.555556 0.666667 0.777778 1 
//change para of B-Spline
n+1	: 5			number of control points.
p	: 3			rank of BSpline.
h	: 3			repeat of head and tail.
nv	: 8			number of node vector.
head vector:
0 0 0 0.25 0.5 1 1 1

相信你们顶点数和曲线阶数一定都能理解意思，那么我来解释一下头节点重数的定义：

头节点重数的作用

头节点重数： 头节点重数是用来描述节点向量头和尾的重合个数的。首先，一个节点向量是单调不减的，而我们讨论的又是均匀节点的 B 样条曲线，所以头节点重数就可以完整的控制节点向量的生成。

而节点向量就能定义控制点对曲线的影响。

下面举两个直观的例子来带你了解头节点重数的作用。
首先我们绘制一个正常的 B 样条曲线，设置它的头节点重数为一：

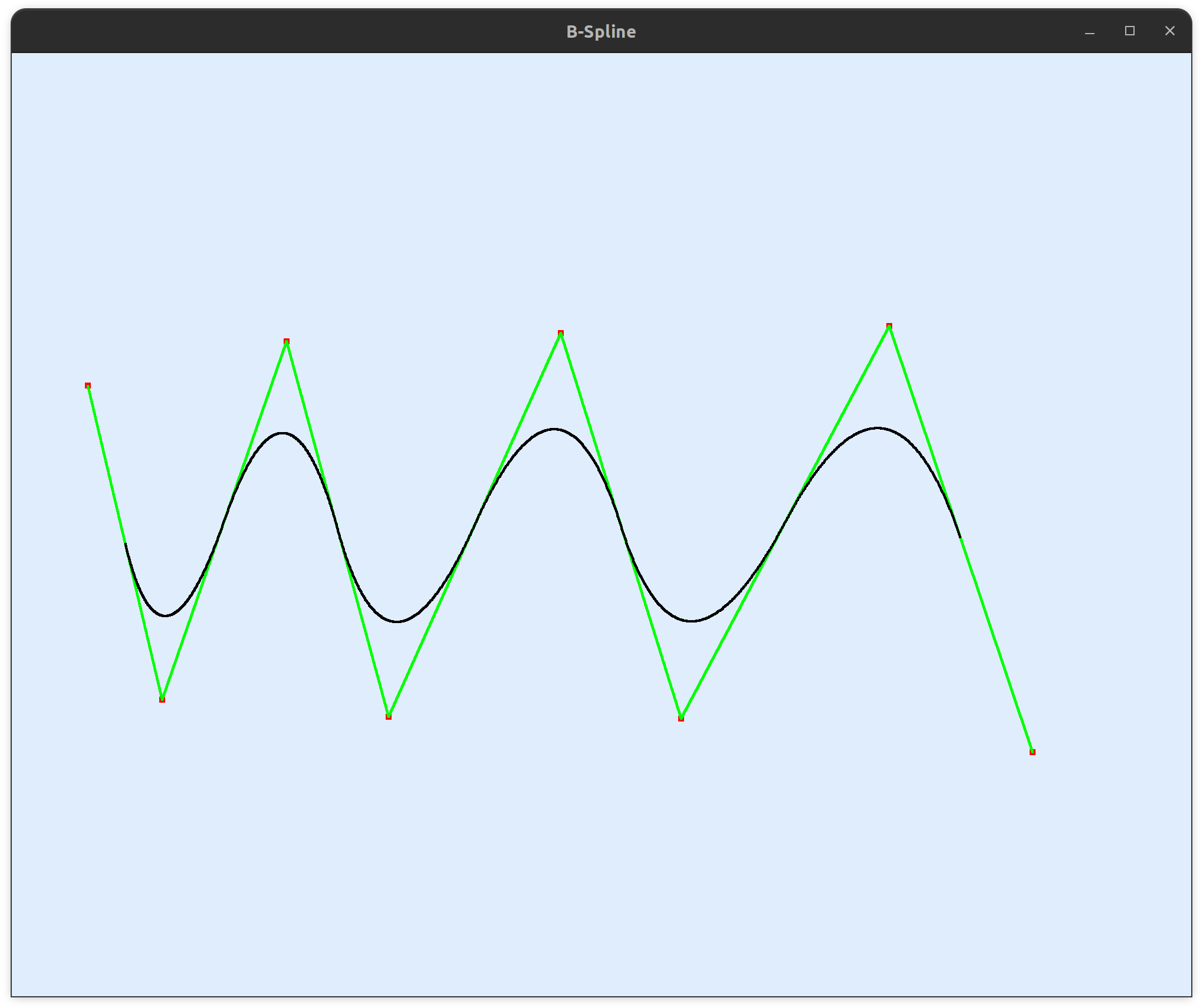
然后我们修改它的头节点重数，使得头节点重数等于基函数阶数。

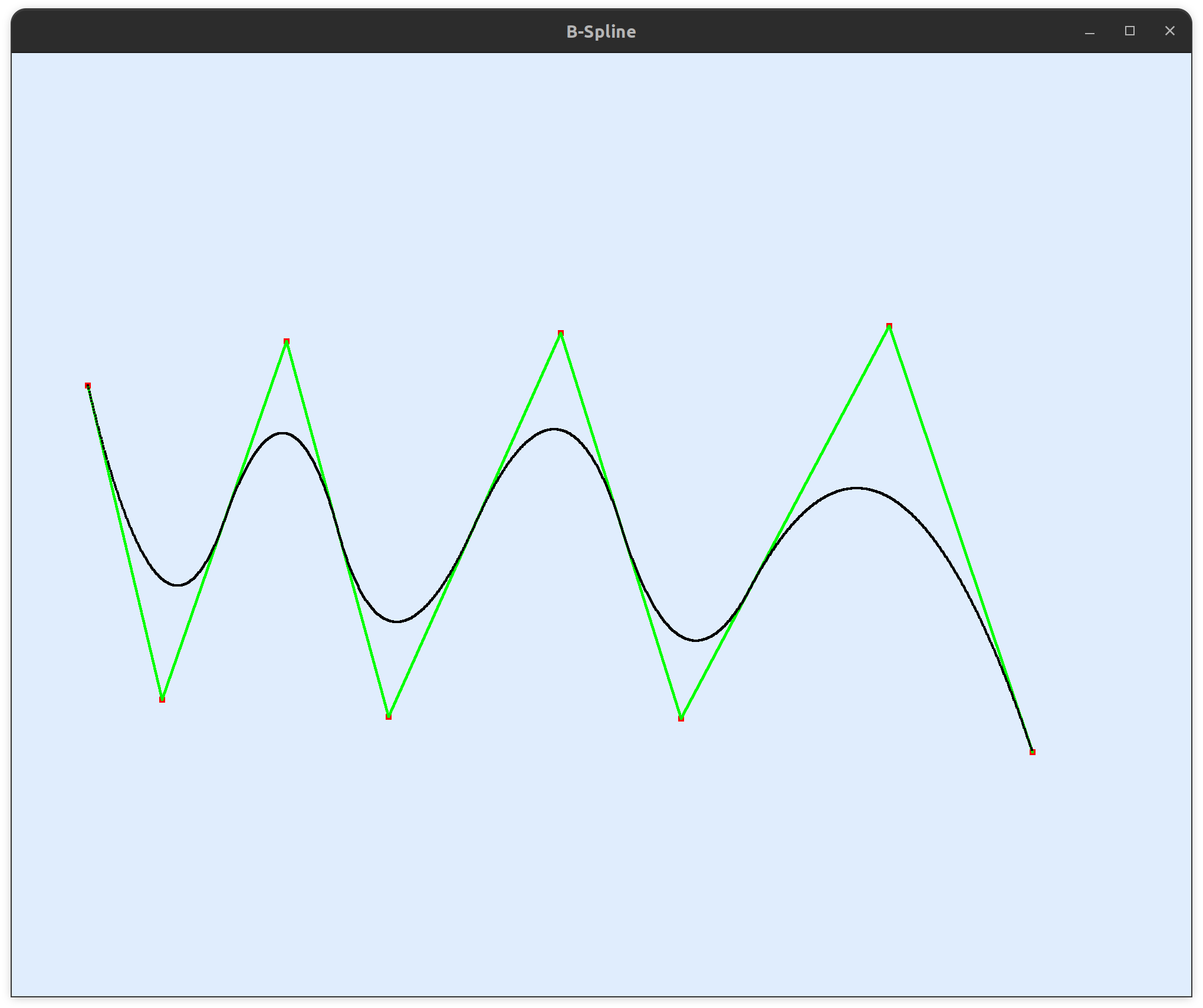
会发现，头节点重数可以使得曲线插值端点。下面我用两个图来从基函数的层面带你理解头节点重数为什么能够影响曲线。首先是一张有五个控制顶点的4阶B样条的基函数关系图。

如果现在让头和尾重合一部分。比如 \(h = p\) 也就是头节点重数等于曲线的阶数。节点向量就会变成下面这样：

\[\begin{cases} u_0 = u_1 = u_2 = u_3 = 0 \\ u_8 = u_ 7 = u_6 = u_5 = 1 \\ u_4 = 0.5 \\ \end{cases} \]

让我们把节点向量的值写到基函数的关系图上去。红色部分的基函数由于区间为零，值恒为零。所以可以看到不为零的基函数构成了伯恩斯坦基函数，也就是Bezier曲线同款基函数。

B样条退化为Bezier曲线

再想象一下，如果控制点的个数减少一个，也就是 \(n+1 = p\) ，控制点的个数等于曲线阶数，并且满足头节点重数等于曲线阶数的时候，中间非零的节点区间只剩下了一个，这个时候，B样条真正的退化为了Bezier曲线。总结一下，B样条退化为Bezier曲线的条件：

• 1.控制顶点个数等于曲线阶数 \(\quad\) \(n+1 = p\)
• 2.头节点重数等于曲线阶数 \(\quad\) \(h = p\)

B样条的实现

这部分其实不难，如果完全理解了B样条真的是非常简单的实现，但是如果不清楚自己是否完全理解了B样条的思想，可以动手实现一下，这里提供实现思路和源代码。这个项目中我用到了几个绘制算法，你无需理解他们是如何工作的，只需要像调用函数一样调用它即可。如果想要使用我的框架进行B样条曲线的学习，请确保自己有看懂C++简单代码的能力，以及稍微阅读一下函数接口的使用。这篇文章会介绍B样条曲线实现用到的所有接口。如果对算法感兴趣的同学也可以去看一下这几个绘制算法的具体实现。
直线的绘制\(\quad\)圆形的绘制\(\quad\)橡皮筋技术

准备工作

请先下载项目源代码，并保证根据README的指导可以让程序跑起来。这个项目提供了linux和windows两个操作系统的编译方案。windows使用VS进行编译，linux使用cmake进行编译。
B-Spline
其中CMakeLists.txt文件的内容如下：

#最低版本
cmake_minimum_required(VERSION 2.8)

#项目信息
project(BSpline)

#查找当前目录下所有源文件
#并将文件名保存在DIR_SOURECE
aux_source_directory(. DIR_SOURCE)
add_executable(${PROJECT_NAME} ${DIR_SOURCE})

find_package(GLUT REQUIRED)
find_package(OpenGL REQUIRED)

if(GLUT_FOUND)
    include_directories(${GLUT_INCLUDE_DIR})
    target_link_libraries(${PROJECT_NAME} ${GLUT_LIBRARIES})
else(GLUT_FOUND)
    message(FATAL_ERROR ”GLUT library not found”)
endif(GLUT_FOUND)
if(OPENGL_FOUND)
    include_directories(${OPENGL_INCLUDE_DIR})
    target_link_libraries(${PROJECT_NAME} ${OPENGL_LIBRARIES})
else(OPENGL_FOUND)
    message(FATAL_ERROR ”OpenGL library not found”)
endif(OPENGL_FOUND)

#指定生成目标

b_spline_basis

这将是我们要实现的第一个函数，b_spline_basis，函数原型如下

GLdouble b_spline_basis(int i, int p, GLdouble u, const vector<GLdouble> &nodeVec)

接受 （i，p，u），返回下标为i的控制点的p阶基函数在参数u处的函数值。
首先编写一阶的基函数。

if (p == 1){
	if (nodeVec[i] <= u && u <= nodeVec[i + 1])
		return 1;
	else
		return 0;
}

在一阶之外的基函数，首先计算两个权值的分母：

GLdouble len1 = nodeVec[i + p - 1] - nodeVec[i];
GLdouble len2 = nodeVec[i + p] - nodeVec[i + 1];

然后利用递归计算两个区间的子基函数

GLdouble alpha, beta;
alpha = (u - nodeVec[i]) / len1;
beta = (nodeVec[i + p] - u) / len2;
return (alpha)*b_spline_basis(i, p - 1, u, nodeVec) + (beta)*b_spline_basis(i + 1, p - 1, u, nodeVec);

由于出现了对len1和len2的除法，所以需要检测区间的长度，避免浮点误差导致的离群点。而且u的区间也不能超过基函数的定义区间，需要把上面代码修改为：

if (u < nodeVec[i] || u > nodeVec[i + p])			//限制参数区间
	return 0;
GLdouble len1 = nodeVec[i + p - 1] - nodeVec[i];
GLdouble len2 = nodeVec[i + p] - nodeVec[i + 1];
GLdouble alpha, beta;
if (len1 <= 1e-10){									//避免浮点误差导致的错误
	alpha = 0;
}
else{
	alpha = (u - nodeVec[i]) / len1;
}
if (len2 <= 1e-10){
	beta = 0;
}
else{
	beta = (nodeVec[i + p] - u) / len2;
}
return (alpha)*b_spline_basis(i, p - 1, u, nodeVec) + (beta)*b_spline_basis(i + 1, p - 1, u, nodeVec);

然后就能得到完整的基函数计算方法了。下面是完整代码的展示。

b_spline_basis

GLdouble b_spline_basis(int i, int p, GLdouble u, const vector<GLdouble> &nodeVec){
	if (p == 1){
		if (nodeVec[i] <= u && u <= nodeVec[i + 1])
			return 1;
		else
			return 0;
	}
	if (u < nodeVec[i] || u > nodeVec[i + p])
		return 0;
	GLdouble len1 = nodeVec[i + p - 1] - nodeVec[i];
	GLdouble len2 = nodeVec[i + p] - nodeVec[i + 1];
	GLdouble alpha, beta;
	if (len1 <= 1e-10){
		alpha = 0;
	}
	 else{
		  alpha = (u - nodeVec[i]) / len1;
	}
	if (len2 <= 1e-10){
		beta = 0;
	}
	else{
		beta = (nodeVec[i + p] - u) / len2;
	}
	return (alpha)*b_spline_basis(i, p - 1, u, nodeVec) + (beta)*b_spline_basis(i + 1, p - 1, u, nodeVec);
}

draw

然后可以开始实现绘制算法了。
绘制算法首先要计算参数对应点的坐标，这个坐标等于每一个控制点在参数u处的贡献。下面代码很好理解，我就只提一点，GLUT的使用。

	GLdouble basis;
	vector<GLdouble> rx(node, 0), ry(node, 0);
	GLdouble u_begin = m_nodeVec[p-1];					//注意开始参数与结尾参数
	GLdouble u_end = m_nodeVec[m_n+1];
	GLdouble dis = (u_end - u_begin) / node;
	GLdouble u = u_begin;
	for (int i = 0; i < node; i++) {
		 for (int j = 0; j <= m_n; j++){
			basis = b_spline_basis(j, p, u, m_nodeVec);
			rx[i] += m_points[j].x * basis;
			ry[i] += m_points[j].y * basis;
		}
	u += dis;
	}
	glBegin(GL_POINTS);
	for (int i = 0; i < node; i++){
		glVertex2d(rx[i], ry[i]);
	}
	glEnd();
	glFlush();

本项目中，只使用了GLUT的点绘制功能，虽然它内置的算法大多比我写的高效，但是毕竟是学习目的，了解绘制算法的底层对自己没有坏处。glVertex2d(int x,int y)可以在屏幕上绘制出一个在(x, y)的点，非常的简单。
好了就讲这么多了，其余的还请大家自己看源代码了，核心代码就这么多了，下次见。白白

后言

如果有小伙伴发现了本文的错误，请您第一时间联系我，我会感激不尽。
作者邮箱：zhywyt@hdu.edu.cn
或者：zhywyt_6.10@qq.com
又或者您可以直接到我的gitee项目中提出issue，我有时间一定会继续更新代码的。