games101 HomeWork2

Games101 HomeWork2

作业要求

rasterize_triangle(): 执行三角形栅格化算法
static bool insideTriangle(): 测试点是否在三角形内。你可以修改此函数的定义，这意味着，你可以按照自己的方式更新返回类型或函数参数。

先从简单的函数开始

insideTriangle

insideTriangle只需要检查点是否在三角形内部，我并没有修改函数的定义，是否在三角形中，返回一个bool 类型的值似乎挺正常的。
判断一个点是否在三角形中其实是挺简单的，这里用了课程中用到的差乘法：

static bool insideTriangle(float x, float y, const Vector3f* _v)
{   
    // TODO : Implement this function to check if the point (x, y) is inside the triangle represented by _v[0], _v[1], _v[2]
    Vector3f P=Vector3f(x,y,_v[0].z());
	//三边向量
    Vector3f AC=_v[2]-_v[0];
    Vector3f CB=_v[1]-_v[2];
    Vector3f BA=_v[0]-_v[1];
    //顶点与目标点向量
	Vector3f AP=P-_v[0];
    Vector3f BP=P-_v[1];
    Vector3f CP=P-_v[2];
    //if cross product in the same direction ,its inside the triangle
    if(AP.cross(AC).dot(BP.cross(BA))>0.0f&&
        BP.cross(BA).dot(CP.cross(CB))>0.0f&&
        CP.cross(CB).dot(AP.cross(AC))>0.0f)
        {
            return true;
        }
        return false;
}

然后是光栅化的实现了

rasterize_triangle

首先我们要找到三角形的一个包围盒(Bunding Box)然后遍历包围盒中的点，如果点在三角形内部，使用重心公式插值得到z值（这部分框架中已经给出实现），并且深度小于z-Buffer中的缓存，那么我们给这个像素的颜色重置为三角形的颜色。

void rst::rasterizer::rasterize_triangle(const Triangle& t) {
    auto v = t.toVector4();
	//包围盒的建立
	std::vector<float> arr_x{t.v[0].x(),t.v[1].x(),t.v[2].x()};
    std::vector<float> arr_y{t.v[0].y(),t.v[1].y(),t.v[2].y()};
    std::sort(arr_x.begin(),arr_x.end());
    std::sort(arr_y.begin(),arr_y.end());

    for(int x=arr_x[0];x<=arr_x[2];x+=1){
        for(int y=arr_y[0];y<arr_y[2];y+=1){
            if(insideTriangle(x+0.5f,y+0.5f,t.v)){
				
				//这里是框架给出的重心公式插值代码
                auto[alpha, beta, gamma] = computeBarycentric2D(x+0.5f, y+0.5f, t.v);
                float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
                float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
                z_interpolated *= w_reciprocal;
				//\end 重心公式插值
                
				//如果目标点的z值（绝对值）小于缓存深度
				if (z_interpolated < depth_buf[get_index(x, y)]) {
                    Eigen::Vector3f point(x, y, 1.0f);
                    set_pixel(point, t.getColor());
					//重置深度缓存颜色
                    depth_buf[get_index(x, y)] = z_interpolated;
                }
            }
        }
    }
}

那么就完成了z-Buffer的步骤，编译运行得到这样的结果注意遮挡顺序，如果你的遮挡顺序错了，请检查你的透视投影矩阵。

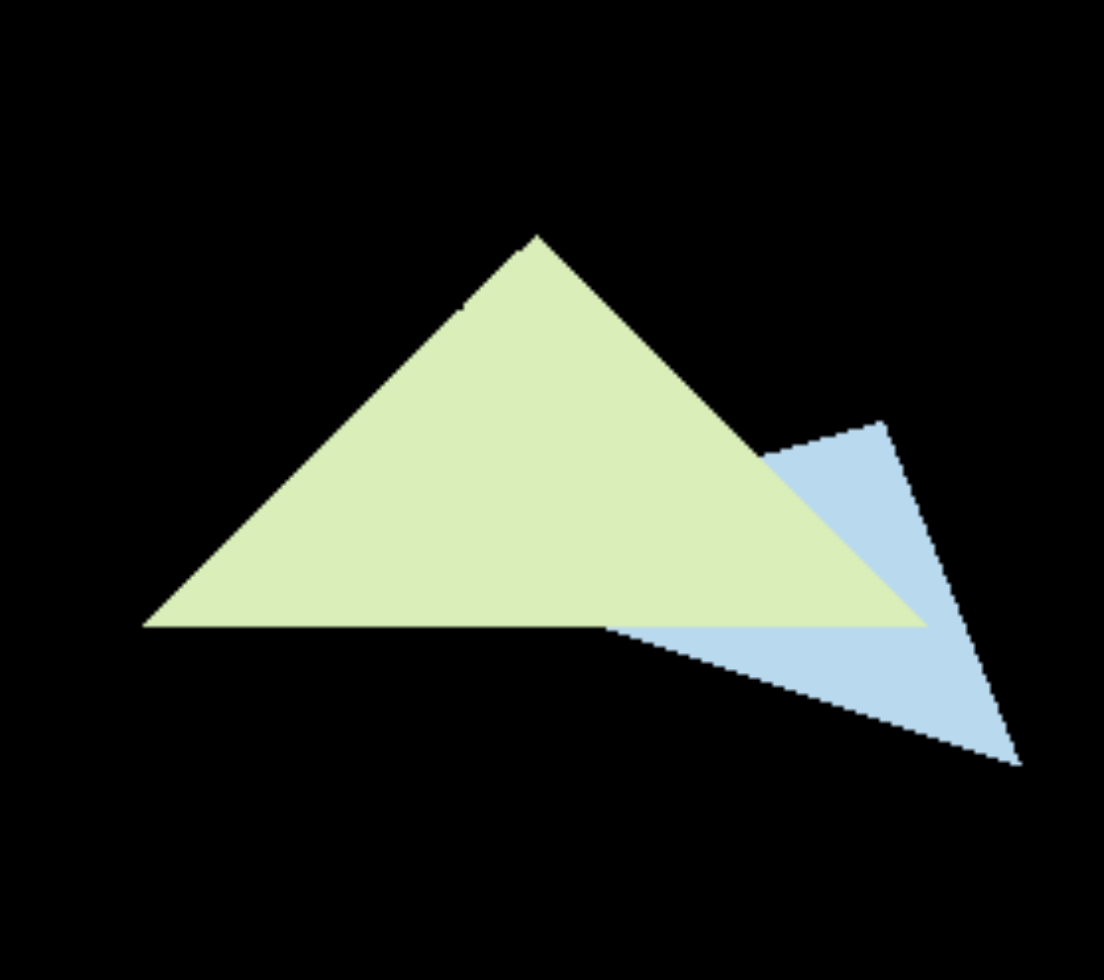
放大可以看到存在明显的锯齿，但是普通要求也到这结束了。

提高题

使用Surper-Sampling对一个像素进2x2超采样。
首先，我们创建两个二维向量来存储深度缓存和颜色缓存。

//rasterizer.hpp
        std::vector<std::array<float,4>> surpersample_corlor_buf;
        std::vector<std::array<float,4>> surpersample_depth_buf;

同时修改构造函数和重置函数

void rst::rasterizer::clear(rst::Buffers buff)
{
    if ((buff & rst::Buffers::Color) == rst::Buffers::Color)
    {
        std::fill(frame_buf.begin(), frame_buf.end(), Eigen::Vector3f{0, 0, 0});
    }
    if ((buff & rst::Buffers::Depth) == rst::Buffers::Depth)
    {
        std::array<float,4> inf;
        inf.fill(std::numeric_limits<float>::infinity()); 
		//DIY
        std::fill(depth_buf.begin(), depth_buf.end(), std::numeric_limits<float>::infinity());
        std::fill(surpersample_depth_buf.begin(), surpersample_depth_buf.end(), inf);
    }
}

rst::rasterizer::rasterizer(int w, int h) : width(w), height(h)
{
    frame_buf.resize(w * h);
    depth_buf.resize(w * h);
	//DIY
    surpersample_corlor_buf.resize(w * h);
    surpersample_depth_buf.resize(w * h);
}

接着就是光栅化的实现了，使用附近四个点是否在三角形内作为参数，设置颜色的值。这里其实是一种不那么严谨的卷机（个人观点），可以让三角形和周围产生的锯齿消失。下面是卷机盒的设计：

代码实现如下：

    for(int i=minX;i<maxX;i++)
    {
        for(int j=minY;j<maxY;j++)
        {
            int Index=get_index(i,j);
            int l=0;
            int IsInTriangleCount=0;
            int IsDontBeCover=0;
            if(IsUseSurperSampling)
            {
                //SurperSampling
                for(auto&k : SampleOffset)
                {
                    float SampleX=i+k.x();
                    float SampleY=j+k.y();
                    if(insideTriangle(SampleX,SampleY,t.v))
                    {
                        auto[alpha, beta, gamma] = computeBarycentric2D(SampleX, SampleY, t.v);
                        float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
                        float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
                        z_interpolated *= w_reciprocal;
                        // check zbuff
                        if(z_interpolated < surpersample_depth_buf[Index][l])
                        {
                            surpersample_depth_buf[Index][l]=z_interpolated;
                            IsDontBeCover++;
                        }
                        IsInTriangleCount++;
                    }
                    l=l+1;
                }
                Vector3f color= t.getColor()*IsInTriangleCount/4.0f;
                if(IsDontBeCover>0)
                {
                    set_pixel(Vector3f(i,j,0),color);
                }
            }
            else
            {
                if(insideTriangle(i+0.5f,j+0.5f,t.v))
                {
                    auto[alpha, beta, gamma] = computeBarycentric2D(i+0.5f, j+0.5f, t.v);
                    float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
                    float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
                    z_interpolated *= w_reciprocal;
                    // check zbuff
                    if(z_interpolated<depth_buf[Index])
                    {
                        depth_buf[Index]=z_interpolated;
                        set_pixel(Vector3f(i,j,1),t.getColor());
					}
                }
            }
        }
    }

最后的输出图片如下，比起超采样之前的三角形，锯齿明显少了。

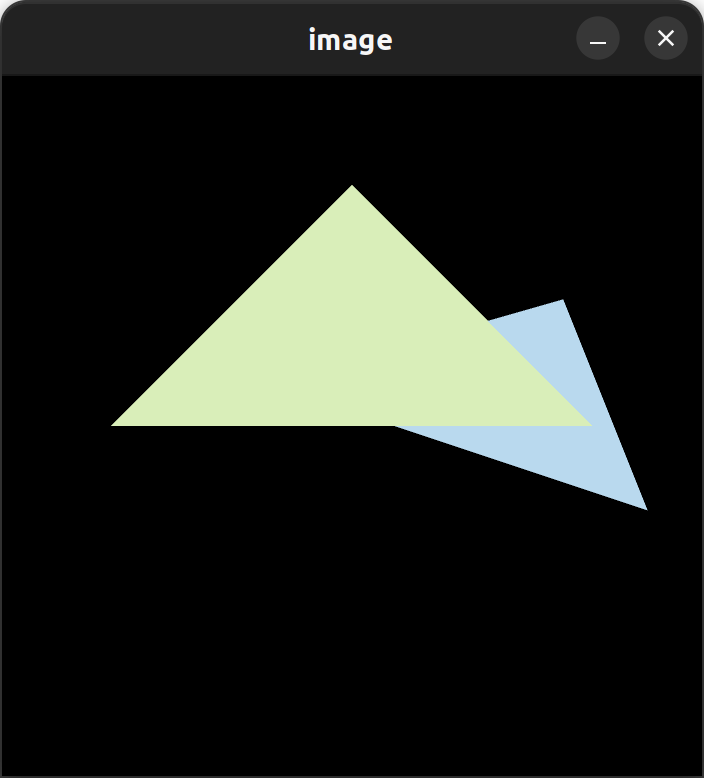
放大后可以看到明显的柔化：

下/上一篇

下一篇：obj导入与phong
上一篇：透视投影矩阵

posted @ 2023-07-24 13:51 zhywyt 阅读(69) 评论(0) 编辑收藏举报

刷新页面返回顶部

zhywyt