games101 HomeWork1
games101 HomeWork 1
说起来我自己写games101的作业也是曲曲折折,虚拟机很卡就拿VS配环境,Windows不会配环境,就装Linux,现在装上了Linux,却因为没有经验把Windows格式化了(我是真的沙比),好在还是开始做了,也挺顺利的,所以再来记录一下作业。
这里是作业框架的下载作业框架下载
导航
基础部分
这里需要完成两个函数,一个是模型变换矩阵,一个是透视投影矩阵。
模型变换矩阵
逐个元素地构建模型变换矩阵并返回该矩阵。在此函数中,你只需要实现三维中绕 z 轴旋转的变换矩阵,而不用处理平移与缩放。
这个部分的实现非常简单,只需要记住这个公式就好了。这里给出绕三个轴旋转的旋转矩阵:
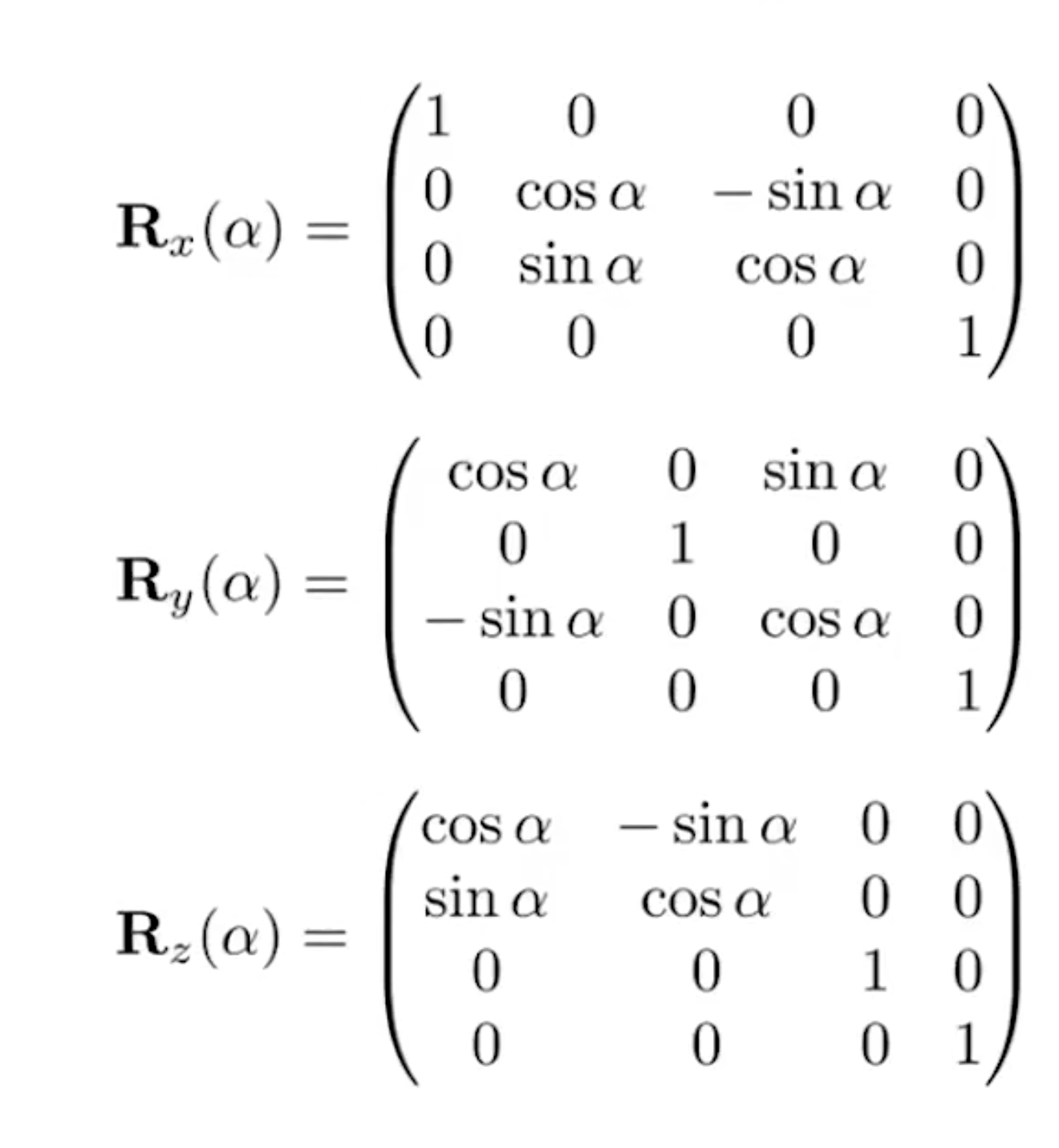
代码实现:
Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
Eigen::Matrix4f model = Eigen::Matrix4f::Identity();
//角度制转弧度制
rotation_angle = rotation_angle / 180.0f * MY_PI;
// TODO: Implement this function
// Create the model matrix for rotating the triangle around the Z axis.
// Then return it.
model << cos(rotation_angle), -sin(rotation_angle), 0, 0,
sin(rotation_angle), cos(rotation_angle), 0, 0,
0, 0, 1, 0,
0, 0, 0, 1;
return model;
}
透视投影矩阵
使用给定的参数逐个元素地构建透视投影矩阵并返回
该矩阵。
这个题目的参数定义其实不是很明显(至少位蒙b了很久),先看一下函数原型:
Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio, float zNear, float zFar)
来解读一下前两个参数,eye_fov指的是摄像机的垂直可视角度,aspect_ratio指的是摄像机的长宽比。使用这四个值也能算出正交投影矩阵。(下图只供参考)
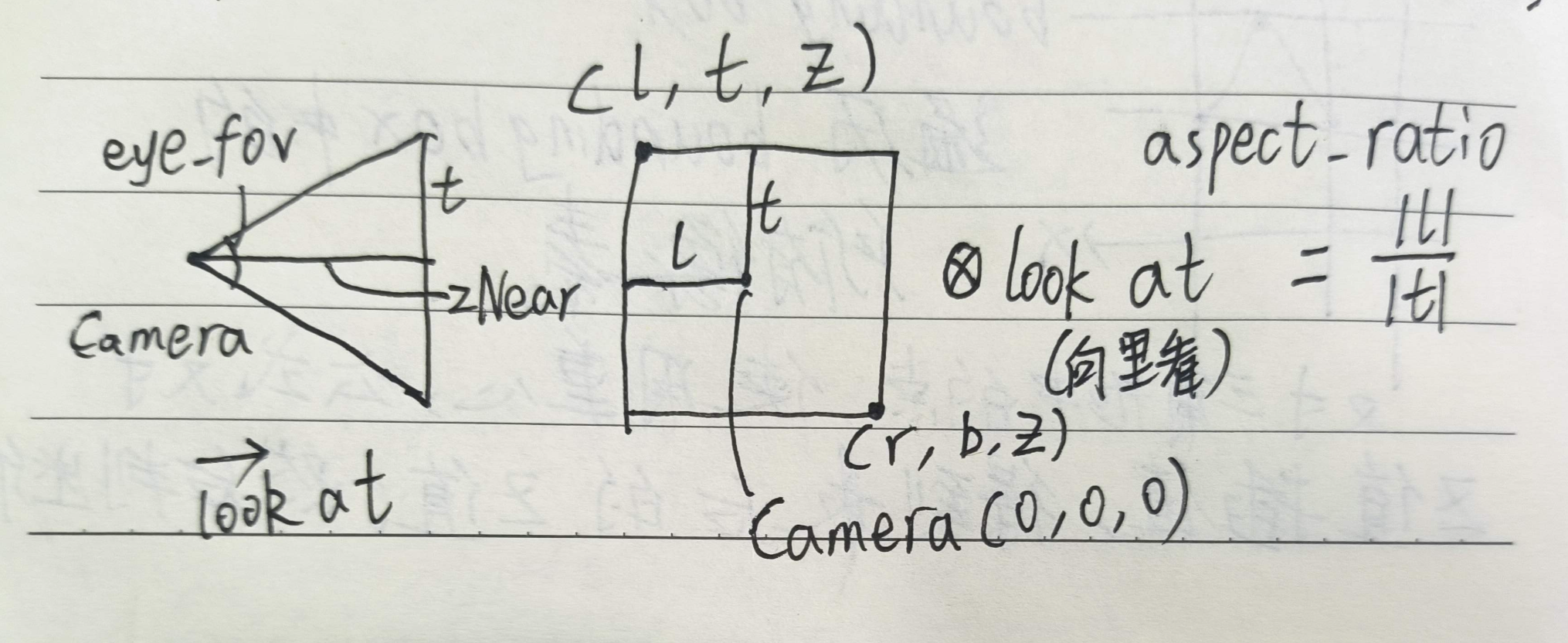
我们从透视投影矩阵开始:
根据课堂上的推导,我们已经知道透视投影矩阵的最终结果,并且所需要的值只有zNear和zFar,于是我们能直接写出这个矩阵:
P << zNear, 0, 0, 0,
0, zNear, 0, 0,
0, 0, zNear + zFar, -zNear * zFar,
0, 0, 1, 0;
然后是我们的正交投影部分了,正交投影需要用到的数据有六个,分别是长方体的参数。
$$[l,r]\times[b,t]\times[f,n]$$
先把正的数据处理掉,直接给出答案,再证明
- \(t=zNear*tan(eye\_fov/2)\)(弧度化后)
- \(r=t*aspect\_ratio\)
另外的l和b分别等于r和t的相反数。
证明如下:(仅供参考)
![image]()
最后还剩下n和f,这两个数和他们的名字差别很大,分别是后和前,赋值的时候需要小心,而且他们的值并不是zNear和zFar分别赋值,而是相反数赋值。如下
f = -zNear;
n = -zFar;
有了数据,我们就可进行投影矩阵的实现了,正交投影矩阵如下:
eye_fov = eye_fov / 180 * MY_PI;
float l, r, b, t, n, f;
//注意这里的f和n代表的意义
f = -zNear;
n = -zFar;
t = -zNear * tan(eye_fov/2);
b = -t;
r = t * aspect_ratio;
l = -r;
S << 2 / (r - l), 0, 0, 0,
0, 2 / (t - b), 0, 0,
0, 0, 2 / (n - f), 0,
0, 0, 0, 1;
M << 1, 0, 0, -(r + l) / 2,
0, 1, 0, -(t + b) / 2,
0, 0, 1, -(n + f) / 2,
0, 0, 0, 1;
//S*M得到正交投影矩阵
普通要求代码汇总
//main.cpp
bool ProjectMode=true;//这是一个控制模式的参数
Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
Eigen::Matrix4f model = Eigen::Matrix4f::Identity();
rotation_angle = rotation_angle / 180.0f * MY_PI;
// TODO: Implement this function
// Create the model matrix for rotating the triangle around the Z axis.
// Then return it.
model << cos(rotation_angle), -sin(rotation_angle), 0, 0,
sin(rotation_angle), cos(rotation_angle), 0, 0,
0, 0, 1, 0,
0, 0, 0, 1;
return model;
}
Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,
float zNear, float zFar)
{
// Students will implement this function
Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();
// TODO: Implement this function
// Create the projection matrix for the given parameters.
// Then return it.
if (!ProjectMode)
{
Eigen::Matrix4f S, M, P;
eye_fov = eye_fov / 180 * MY_PI;
float l, r, b, t, n, f;
//注意这里的f和n代表的意义
f = -zNear;
n = -zFar;
t = -zNear * tan(eye_fov/2);
b = -t;
r = t * aspect_ratio;
l = -r;
S << 2 / (r - l), 0, 0, 0,
0, 2 / (t - b), 0, 0,
0, 0, 2 / (n - f), 0,
0, 0, 0, 1;
M << 1, 0, 0, -(r + l) / 2,
0, 1, 0, -(t + b) / 2,
0, 0, 1, -(n + f) / 2,
0, 0, 0, 1;
P << zNear, 0, 0, 0,
0, zNear, 0, 0,
0, 0, zNear + zFar, -zNear * zFar,
0, 0, 1, 0;
return S * M * P;
}
else//这是精简版本
{
eye_fov = eye_fov / 180 * MY_PI;
projection << 1 / (aspect_ratio * tan(eye_fov / 2.0f)), 0, 0, 0,
0, 1 / tan(eye_fov / 2.0f), 0, 0,
0, 0, -(zFar + zNear) / (zFar - zNear), 2 * zFar * zNear / (zNear - zFar),
0, 0, -1, 0;
return projection;
}
}
提升部分
提升部分要求:在 main.cpp 中构造一个函数,该函数的作用是得到绕任意
过原点的轴的旋转变换矩阵。根据101中的推导,我们需要计算的东西并不多,按要求写好就行了。我选择重载get_model_matrix函数,来实现任意旋转轴的旋转操作。
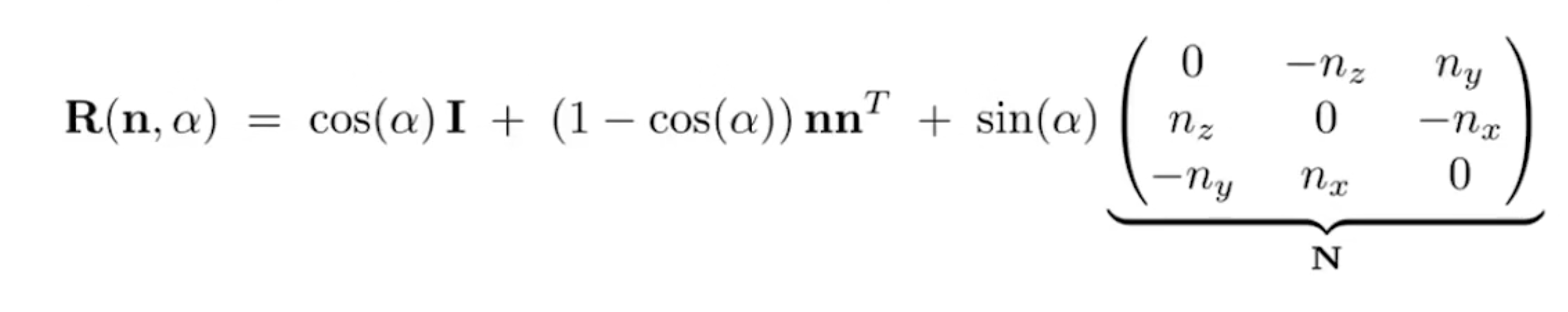
Eigen::Matrix4f get_rotation(Vector3f axis, float rotation_angle)
{
rotation_angle = rotation_angle / 180.0f * MY_PI;
Eigen::Matrix4f Result = Eigen::Matrix4f::Identity();
Eigen::Matrix3f I = Eigen::Matrix3f::Identity();//单位矩阵
Eigen::Matrix3f N = Eigen::Matrix3f::Identity();
Eigen::Matrix3f ResultMat3 = Eigen::Matrix3f::Identity();
N << 0, -axis[2], axis[1],
axis[2], 0, -axis[0],
-axis[1], axis[0], 0;
ResultMat3 = I * cos(rotation_angle) + (1 - cos(rotation_angle)) * axis * axis.transpose() + sin(rotation_angle) * N;
Result << ResultMat3(0, 0), ResultMat3(0, 1), ResultMat3(0, 2), 0,
ResultMat3(1, 0), ResultMat3(1, 1), ResultMat3(1, 2), 0,
ResultMat3(2, 0), ResultMat3(2, 1), ResultMat3(2, 2), 0,
0, 0, 0, 1;
return Result;
}
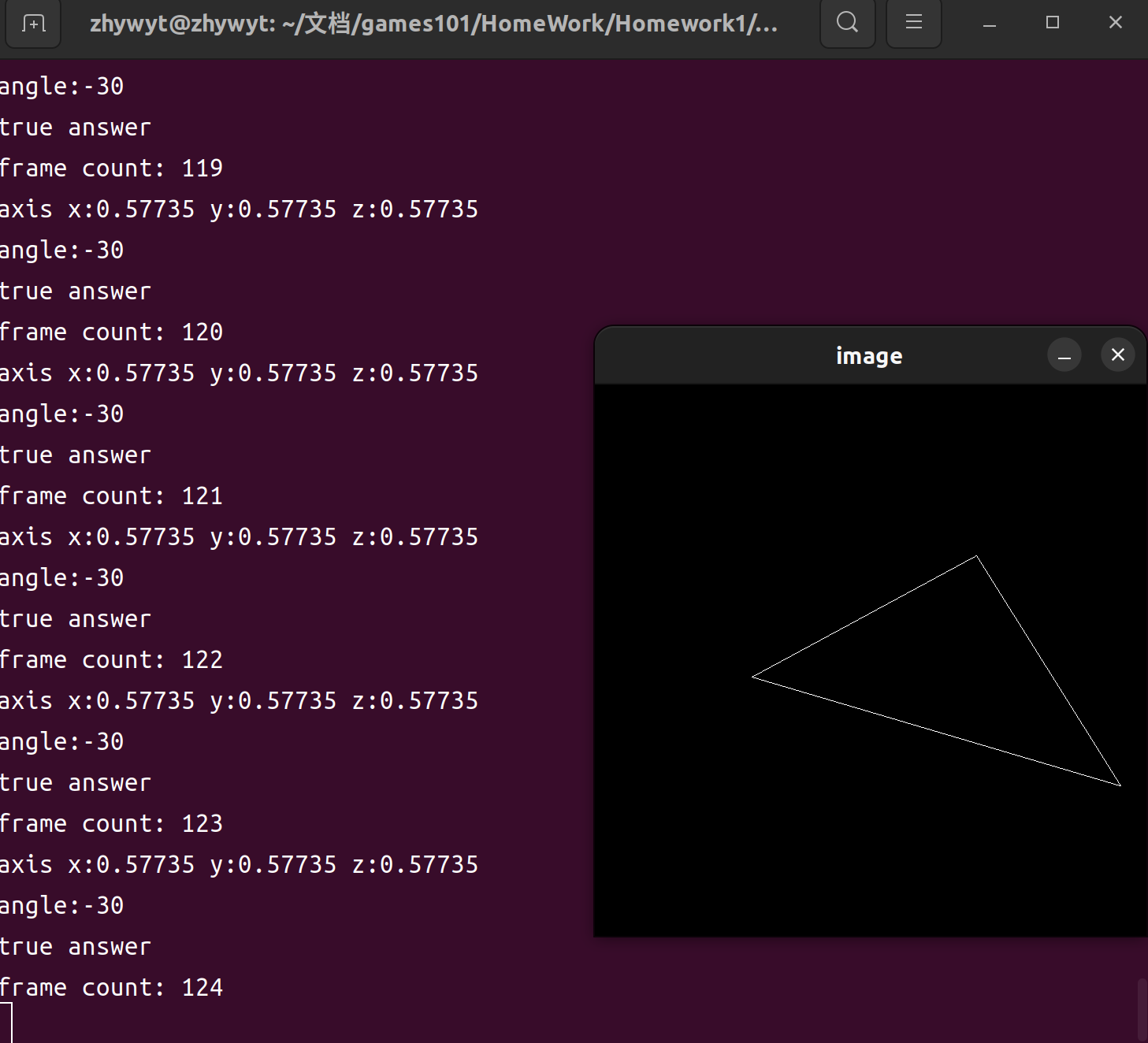
其余代码和普通要求一致。得到结果如下:
结果
因为是第一次作业,所以我这里给出编译的操作:
先来到作业目录

创建build文件夹
来到build文件夹
使用上级目录创建项目文件
构建编译,这里的-j8是表示调用的核心数量,最后一句target Rasterizer表示可执行文件为Rasterizer
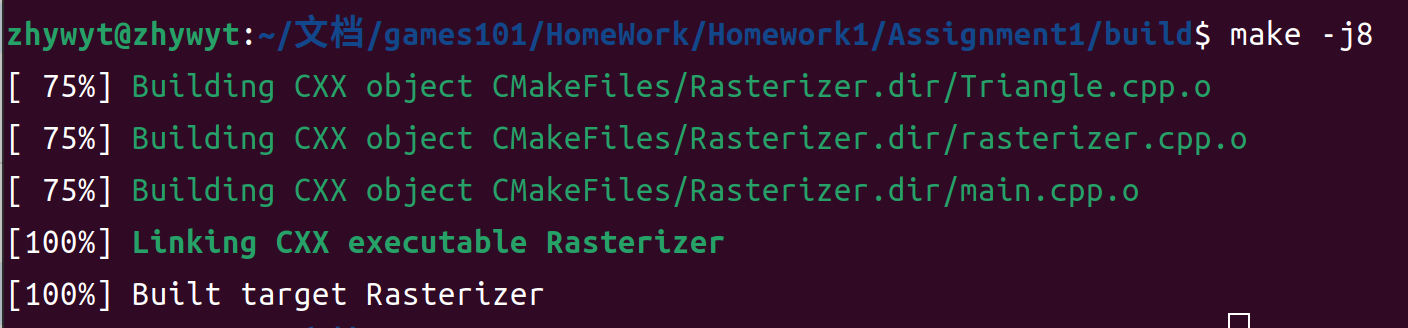
运行

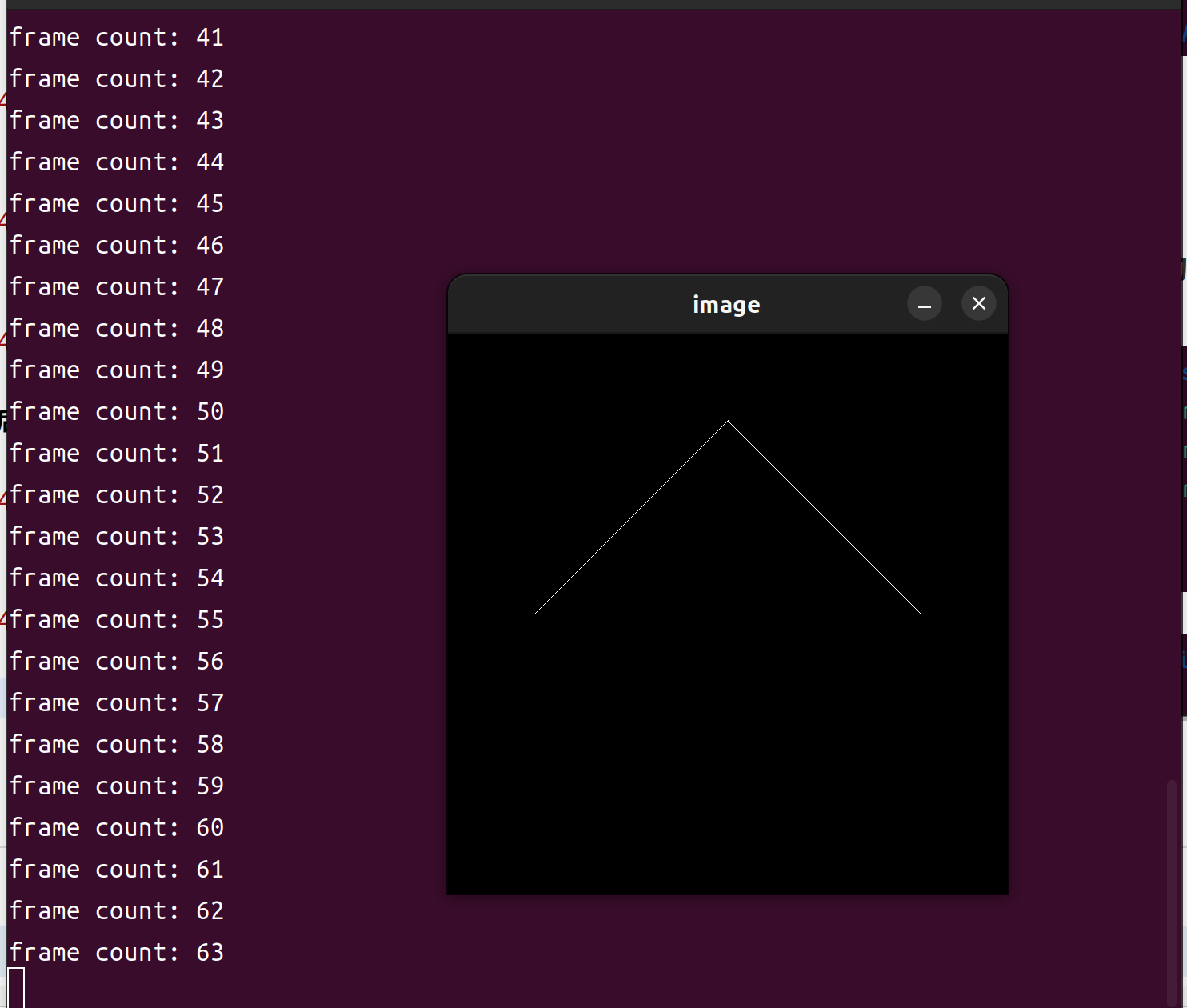
按下Esc或者Ctrl+C停止
全部指令汇总
mkdir build
cd build
cmake ..
make -j8
./Rasterizer
普通要求
运行指令与结果
./Rasterizer 不带参数运行

./Rasterizer -r 0 output.png无旋转保存图片


./Rasterizer -r 90 output90.png旋转保存图片

提升要求
先介绍一下main函数的两个参数argc和argv
argc全称arugment count,表示调用程序的时候,传入的参数的个数。argv全称argument vector,表示调用程序的时候,传入的参数向量,类型为字符串
默认的,argv[0]是调用程序的完整路径,然后argv[0]-argv[argc-1]都是可以访问的字符串。在程序中,我们可以使用标准库定义的stof函数,把字符串转成浮点型,或者使用stod把字符串转化成整形。知道这一点之后,我们就可以设计一个main函数来把我们自定义的旋转轴作为参数传入程序了。
这里是我自己设计的一个传参方案,有兴趣的可以读一下程序。
main.cpp
#include "Triangle.hpp"
#include "rasterizer.hpp"
#include <eigen3/Eigen/Eigen>
#include <iostream>
#include <opencv2/opencv.hpp>
constexpr double MY_PI = 3.1415926;
bool ProjectMode=true;
Eigen::Matrix4f get_view_matrix(Eigen::Vector3f eye_pos)
{
Eigen::Matrix4f view = Eigen::Matrix4f::Identity();
Eigen::Matrix4f translate;
translate << 1, 0, 0, -eye_pos[0], 0, 1, 0, -eye_pos[1], 0, 0, 1,
-eye_pos[2], 0, 0, 0, 1;
view = translate * view;
return view;
}
Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
Eigen::Matrix4f model = Eigen::Matrix4f::Identity();
rotation_angle = rotation_angle / 180.0f * MY_PI;
// TODO: Implement this function
// Create the model matrix for rotating the triangle around the Z axis.
// Then return it.
model << cos(rotation_angle), -sin(rotation_angle), 0, 0,
sin(rotation_angle), cos(rotation_angle), 0, 0,
0, 0, 1, 0,
0, 0, 0, 1;
return model;
}
// Rodrigues rotation formula
Eigen::Matrix4f get_rotation(Vector3f axis, float angle)
{
angle = angle / 180.0f * MY_PI;
Eigen::Matrix4f Result = Eigen::Matrix4f::Identity();
Eigen::Matrix3f E = Eigen::Matrix3f::Identity();
Eigen::Matrix3f N = Eigen::Matrix3f::Identity();
Eigen::Matrix3f ResultMat3 = Eigen::Matrix3f::Identity();
N << 0, -axis[2], axis[1],
axis[2], 0, -axis[0],
-axis[1], axis[0], 0;
ResultMat3 = E * cos(angle) + (1 - cos(angle)) * axis * axis.transpose() + sin(angle) * N;
Result << ResultMat3(0, 0), ResultMat3(0, 1), ResultMat3(0, 2), 0,
ResultMat3(1, 0), ResultMat3(1, 1), ResultMat3(1, 2), 0,
ResultMat3(2, 0), ResultMat3(2, 1), ResultMat3(2, 2), 0,
0, 0, 0, 1;
return Result;
}
Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,
float zNear, float zFar)
{
// Students will implement this function
Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();
// TODO: Implement this function
// Create the projection matrix for the given parameters.
// Then return it.
if (!ProjectMode)
{
std::cout<<"Protable answer"<<std::endl;
Eigen::Matrix4f S, M, P;
eye_fov = eye_fov / 180 * MY_PI;
float l, r, b, t, n, f;
//注意这里的f和n代表的意义
f = -zNear;
n = -zFar;
t = -zNear * tan(eye_fov/2);
b = -t;
r = t * aspect_ratio;
l = -r;
S << 2 / (r - l), 0, 0, 0,
0, 2 / (t - b), 0, 0,
0, 0, 2 / (n - f), 0,
0, 0, 0, 1;
M << 1, 0, 0, -(r + l) / 2,
0, 1, 0, -(t + b) / 2,
0, 0, 1, -(n + f) / 2,
0, 0, 0, 1;
P << zNear, 0, 0, 0,
0, zNear, 0, 0,
0, 0, zNear + zFar, -zNear * zFar,
0, 0, 1, 0;
return S * M * P;
}
else
{
std::cout<<"true answer"<<std::endl;
eye_fov = eye_fov / 180 * MY_PI;
projection << 1 / (aspect_ratio * tan(eye_fov / 2.0f)), 0, 0, 0,
0, 1 / tan(eye_fov / 2.0f), 0, 0,
0, 0, -(zFar + zNear) / (zFar - zNear), 2 * zFar * zNear / (zNear - zFar),
0, 0, -1, 0;
return projection;
}
}
int main(int argc, const char **argv)
{
float angle = 0;
bool command_line = false;
Eigen::Vector3f axis = Eigen::Vector3f(0.f, 1.f, 0.f);
std::string filename = "output.png";
if(argc>=2){
std::cout<<argv[1]<<std::endl;
if(argv[1][1]=='m')//使用精简版本
ProjectMode=true;
else if(argv[1][1]=='p')//使用便阅读版本
ProjectMode=false;
std::cout<<ProjectMode<<std::endl;
}
if (argc >= 3)
{
std::cout<<argc<<std::endl;
angle = std::stof(argv[2]); // -r by default
if (argc == 4)
{
command_line = true;
filename = std::string(argv[3]);
}
else if(argc==6){//DIY(
axis.x()=std::stof(argv[3]);
axis.y()=std::stof(argv[4]);
axis.z()=std::stof(argv[5]);
axis.normalize();
}
//
}
rst::rasterizer r(700, 700);
Eigen::Vector3f eye_pos = {0, 0, 5};
std::vector<Eigen::Vector3f> pos{{2, 0, -2}, {0, 2, -2}, {-2, 0, -2}};
std::vector<Eigen::Vector3i> ind{{0, 1, 2}};
auto pos_id = r.load_positions(pos);
auto ind_id = r.load_indices(ind);
int key = 0;
int frame_count = 0;
if (command_line)
{
r.clear(rst::Buffers::Color | rst::Buffers::Depth);
r.set_model(get_model_matrix(angle));
r.set_view(get_view_matrix(eye_pos));
r.set_projection(get_projection_matrix(45, 1, 0.1, 50));
r.draw(pos_id, ind_id, rst::Primitive::Triangle);
cv::Mat image(700, 700, CV_32FC3, r.frame_buffer().data());
image.convertTo(image, CV_8UC3, 1.0f);
cv::imwrite(filename, image);
return 0;
}
while (key != 27)
{
r.clear(rst::Buffers::Color | rst::Buffers::Depth);
r.set_model(get_model_matrix(angle));
//DIY
if (argc == 6){
r.set_model(get_rotation(axis, angle));
std::cout<<"axis x:"<<axis.x()<<" y:"<<axis.y()<<" z:"<<axis.z()<<std::endl<<"angle:"<<angle<<std::endl;
}
//
r.set_view(get_view_matrix(eye_pos));
r.set_projection(get_projection_matrix(45, 1, 0.1, 50));
r.draw(pos_id, ind_id, rst::Primitive::Triangle);
cv::Mat image(700, 700, CV_32FC3, r.frame_buffer().data());
image.convertTo(image, CV_8UC3, 1.0f);
cv::imshow("image", image);
key = cv::waitKey(10);
std::cout << "frame count: " << frame_count++ << '\n';
if (key == 'a')
{
angle += 10;
}
else if (key == 'd')
{
angle -= 10;
}
}
return 0;
}
部分效果如下:
可执行操作如下
./Rasterizer -p使用便阅读版本矩阵进行计算./Rasterizer -m使用简便版本矩阵进行计算
![image]()
![image]()
games101 Hw1 到此就结束啦!
2023.8.17
写完之后,感觉少了点什么,于是便有了下面的东西。
框架解读
作业一的文件如下
- main.cpp
- rasterizer.cpp
- rasterizer.hpp
- Triangle.cpp
- Triangle.hpp
读框架代码要从接口开始,也就是头文件,我们先注意一下各个头文件的引用情况:
---------------------------------------------
//main
#include "Triangle.hpp"
#include "rasterizer.hpp"
#include <eigen3/Eigen/Eigen>
#include <iostream>
#include <opencv2/opencv.hpp>
---------------------------------------------
//raserizer.hpp
#include "Triangle.hpp"
#include <algorithm>
#include <eigen3/Eigen/Eigen>
using namespace Eigen;
---------------------------------------------
//Triangle.hpp
#include <eigen3/Eigen/Eigen>
using namespace Eigen;
---------------------------------------------
可以看到,Triangle.hpp是一个独立的类,只需要依赖数学库Eigen,我们从这个三角形类开始。
Triangle
数据成员
这里用到的三角形类存储了一个三角形的顶点部分信息,以达到绘制一个线框所需要的数据结构。具体有这些:
Vector3f v[3];顶点坐标Vector3f color[3];顶点颜色Vector2f tex_coords[3];纹理坐标Vector3f normal[3];法线方向
其中只有顶点坐标在作业一中用到了。
接口函数
//访问顶点坐标
Eigen::Vector3f a() const { return v[0]; }
Eigen::Vector3f b() const { return v[1]; }
Eigen::Vector3f c() const { return v[2]; }
//设置顶点坐标、法线、颜色、纹理坐标
void setVertex(int ind, Vector3f ver); /*set i-th vertex coordinates */
void setNormal(int ind, Vector3f n); /*set i-th vertex normal vector*/
void setColor(int ind, float r, float g, float b); /*set i-th vertex color*/
void setTexCoord(int ind, float s,
float t); /*set i-th vertex texture coordinate*/
//到Vec4的转化,方便进行矩阵计算
std::array<Vector4f, 3> toVector4() const;
函数实现
只有一个函数是值的讲解的toVector4:这个函数把三角形顶点坐标转化为齐次坐标后返回。
std::transform是一个通用算法,用于对输入范围中的元素执行给定的操作,并将结果存储在输出范围中。在这个例子中,我们使用std::transform(std::begin(v), std::end(v), res.begin(), [](auto& vec) { ... })来将v数组中的每个Vector4f对象转换为res数组中的对应对象。[](auto& vec) { ... }是一个lambda表达式,用于定义转换操作。
std::array<Vector4f, 3> Triangle::toVector4() const
{
std::array<Vector4f, 3> res;
std::transform(std::begin(v), std::end(v), res.begin(), [](auto& vec) {
return Vector4f(vec.x(), vec.y(), vec.z(), 1.f);
});
return res;
}
rasterizer
这个类就很有意思了,从类的数据成员开始看:
class rasterizer
{
private:
//三个投影矩阵
Eigen::Matrix4f model;
Eigen::Matrix4f view;
Eigen::Matrix4f projection;
//顶点缓存
std::map<int, std::vector<Eigen::Vector3f>> pos_buf;
std::map<int, std::vector<Eigen::Vector3i>> ind_buf;
//颜色缓存
std::vector<Eigen::Vector3f> frame_buf;
//深度缓存 暂未使用
std::vector<float> depth_buf;
//显示区域参数
int width, height;
//工具
int next_id = 0;
};
frame_buf存储的是最后的颜色结果,虽然直译是指框架缓存。(英语不好,勿喷)
有了这些数据成员,就开开始写数据的构造和赋值了。构造只有对显示区域参数的初始化:
构造
//raterizer.cpp
rst::rasterizer::rasterizer(int w, int h) : width(w), height(h)
{
frame_buf.resize(w * h);
depth_buf.resize(w * h);
}
赋值
需要外部输入的数据成员还有
- model
- view
- projection
- pos_buf
- ind_buf
void rst::rasterizer::set_model(const Eigen::Matrix4f& m){
model = m;
}
void rst::rasterizer::set_view(const Eigen::Matrix4f& v){
view = v;
}
void rst::rasterizer::set_projection(const Eigen::Matrix4f& p){
projection = p;
}
//导入顶点坐标和顶点索引
rst::pos_buf_id rst::rasterizer::load_positions(const std::vector<Eigen::Vector3f> &positions){
auto id = get_next_id();
pos_buf.emplace(id, positions);
return {id};
}
rst::ind_buf_id rst::rasterizer::load_indices(const std::vector<Eigen::Vector3i> &indices){
auto id = get_next_id();
ind_buf.emplace(id, indices);
return {id};
}
上面三个MVP函数是非常简单的,没什么好讲的,但是导入顶点坐标和索引的函数,可得好好讲讲。
首先是为什么这个两个函数返回值分别是rst::pos_buf_id和rst::ind_buf_id ,在原代码框架里给了这么一段解释:
/*
For the curious : The draw function takes two buffer id's as its arguments.
These two structs make sure that if you mix up with their orders, the
compiler won't compile it. Aka : Type safety
*/
/*
对于感兴趣的人 : draw 函数接受两个缓冲区ID作为参数。
这些两个结构体确保如果将它们顺序混乱,编译器不会编译它。
又名 : 类型安全
*/
struct pos_buf_id{
int pos_id = 0;
};
struct ind_buf_id{
int ind_id = 0;
};
在我们的draw函数里面,直接对id进行了下标访问,因为我们不希望再去浪费查找的时间,这样一个设计可以让程序高效而安全。这就像是给一个整形变量贴上了标签一样。两个不同的返回值类型的存在,使得我们可以存在相同的id在pos_buf和ind_buf中,而不会产生问题。
而至于为什么要返回这么一个值呢?
这是因为我们在使用rasterizer类的时候,需要获得导入数据的控制buf_id,才能对导入的数据进行访问。
输出
数据成员的初始化和赋值都已经解决了,接下来就是如何准确的进行光栅化的问题了。光栅化要做的事情就两件,一、把颜色缓存填充好;二、深度缓存填充好。
一、颜色缓存
首先实现一个填充颜色的小函数rst::rasterizer::set_pixel(const Eigen::Vector3f& point, const Eigen::Vector3f& color)
作为rst::rasterizer 类的成员函数,他需要设置指定点的颜色,但是注意frame_buf是一个数组,数组意味着越界的风险,所以需要在设置之前判断下标的位置。
if (point.x() < 0 || point.x() >= width ||
point.y() < 0 || point.y() >= height) return;
auto ind = (height-point.y())*width + point.x();
frame_buf[ind] = color;
二、深度缓存
这个作业没有涉及到深度缓存,因为绘制的是一个平面的三角形,所以深度缓存留到下一次作业讲解。
本文来自博客园,作者:zhywyt,转载请注明原文链接:https://www.cnblogs.com/zhywyt/p/17575190.html


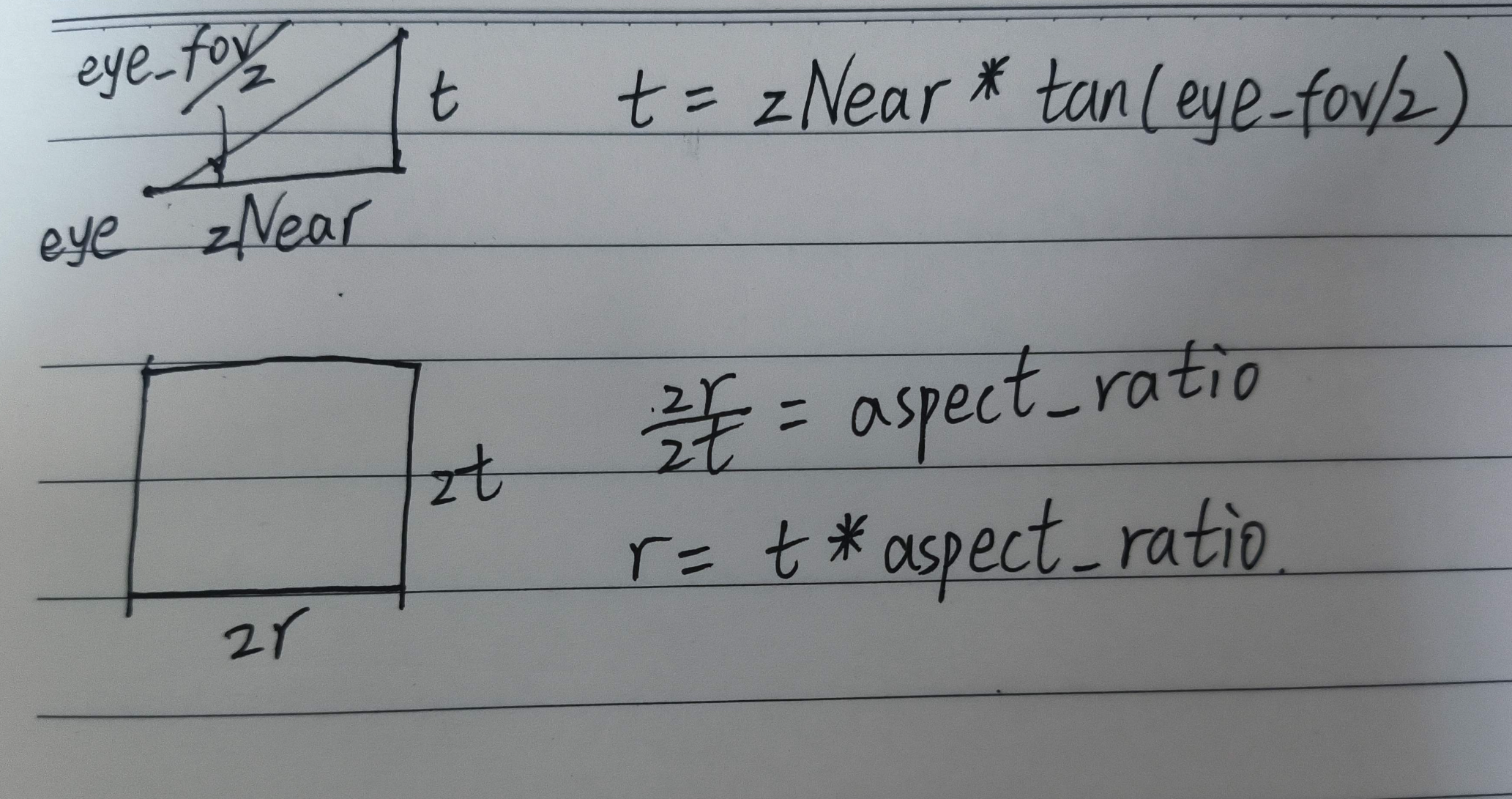

 浙公网安备 33010602011771号
浙公网安备 33010602011771号