【Luogu P1661】扩散

题目：

一个点每过一个单位时间就会向四个方向扩散一个距离，如图。

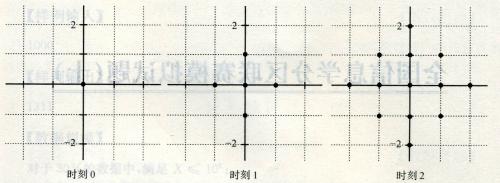
两个点$a$、$b$连通，记作$e(a,b)$,当且仅当$a$、$b$的扩散区域有公共部分。连通块的定义是块内的任意两个点$u$、$v$都必定存在路径$e(u,a_0),e(a_0,a_1),\cdots,e(a_k,v)$。给定平面上的$n$个点，问最早什么时刻它们形成一个连通块。

分析：

一看$n\lt 50$？随便搞即可。

考虑若$n\lt 10^3$怎么做。

考虑每个点$(x_1,y_1)$和$(x_2,y_2)$形成联通块所需要的时间为

$$\frac{|x_1-x_2|+|y_1-y_2|}{2}$$

故我们需要求一个生成树，其中对于每个点$(u,v)$，$\frac{|x_u-x_v|+|y_u-y_v|}{2}$最小。

$\rm Kruskal$算法即可，时间复杂度$O(n^2\log n^2)$。

#include <bits/stdc++.h>

using namespace std;

const int MAXN = 55;

int fa[MAXN], x[MAXN], y[MAXN], n, tot = 0, maxn = 0;

int find(int x) {
    return fa[x] == x ? fa[x] : (fa[x] = find(fa[x]));
}

void merge(int x, int y) {
    fa[find(y)] = find(x);
}

struct edge {
    int from, to;
    
    edge() {
        
    }
    edge(int jbk, int stt) {
        from = jbk; to = stt;
    }
} edges[MAXN * MAXN];

int ha(edge a) {
    return abs(x[a.from] - x[a.to]) + abs(y[a.from] - y[a.to]);
}

bool cmp(edge a, edge b) {
    return ha(a) < ha(b);
}

int main() {
    ios::sync_with_stdio(false);
    cin >> n;
    for(int i = 0; i < n; i++)
        fa[i] = i;
    for(int i = 0; i < n; i++) {
        cin >> x[i] >> y[i];
    }
    for(int i = 0; i < n; i++)
        for(int j = 0; j < i; j++) {
            edge v(i, j);
            edges[tot++] = v;
        }
    sort(edges, edges + tot, cmp);
    for(int i = 0; i < tot; i++)
        if(find(edges[i].from) != find(edges[i].to)) {
            maxn = max(ha(edges[i]), maxn);
            merge(edges[i].from, edges[i].to);
        }
    cout << (int)(ceil(maxn / 2.0)) << endl;
    return 0;
}