随机算法学习笔记

随机算法

数值概率算法

数值概率算法是一类用于数值问题求解的算法。

例1 计算面积

给定平面上的一个封闭图形，求它的面积。

你可以调用函数 \(f(x,y)\) 返回这个地方是否在这个图形内。

保证这个封闭图形的任何一个点在的坐标 \((x,y), 0\le x,y\le1\)。

分析

随机在 \(x,y\) 范围的正方形内取若干个点，判断是否在图形内，计算落在该图形内概率 \(P\)，面积为 \(1^2P\)。

爬山算法

思路

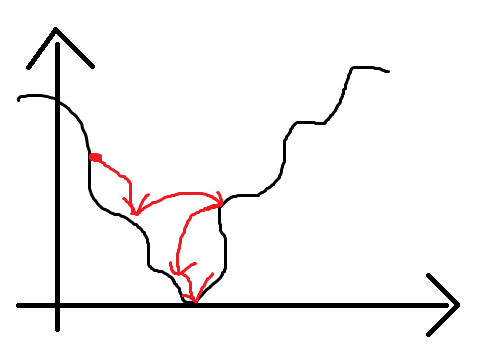
爬山算法，为了找出一个函数的最大/最小值，随机一个初始点作为当前最优解，每次随机选择附近的一个新点，然后如果该点的值比当前点的值更优，就把新点设为当前点。

缺点

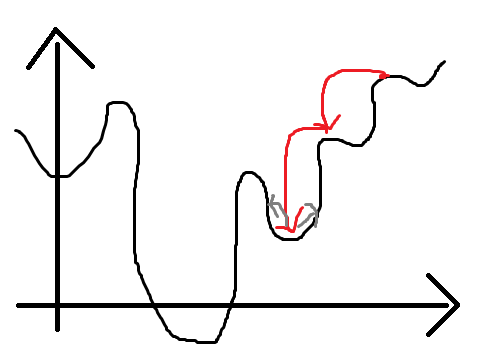
有可能落入一个局部最优值，出不来。

模拟退火

思路

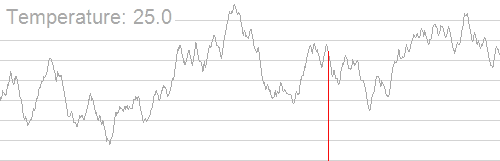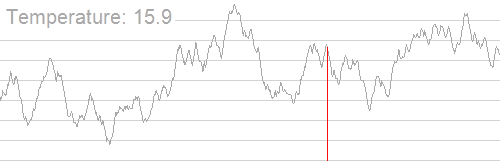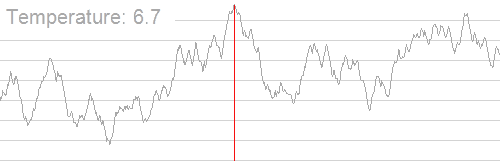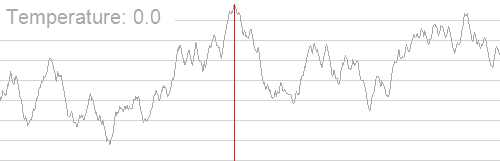
模拟退火的出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。模拟退火算法是一种通用的优化算法，其物理退火过程由加温过程、等温过程、冷却过程这三部分组成。——百度百科

其思路与爬山算法差不多，只不过它在选择新的解的时候，若新解比旧解劣，以一定的概率接受新解。

这个概率会随着“温度”的减少越来越低。（温度随着迭代逐渐降低）

通常，若温度为 \(T\)，新解与旧解的差为 \(\Delta t'\)，按照 Metropolis 准则，接收新解的概率为 \(e^{\frac{\Delta t'} T}\)。

习题

题1 [HAOI2006]均分数据

已知数列 \(a\)，把 \(a\) 分为 \(m\) 组数据，使得各组数据的和的均方差最小。

题2 计算定积分

给定 \(f(x),a,b\)，求 \(\int_b^a f(x)dx\)，满足 $0\le a,b\le 1, \forall a\le x \le b,0<f(x)\le1011 $，精确到 \(3\) 位小数。（假设你不知道定积分怎么做）