OO第一单元作业总结
第一单元的学习,感觉是一个JAVA语言和面向对象入门的学习。在课下,我们主要完成了三次表达式求导的作业,从最开始的简单多项式求导到第三次作业允许三角函数内有嵌套因子的求导,难度依次递进。
- 一、程序结构分析
1.第一次作业
第一次作业要求是简单多项式的导函数的求解。
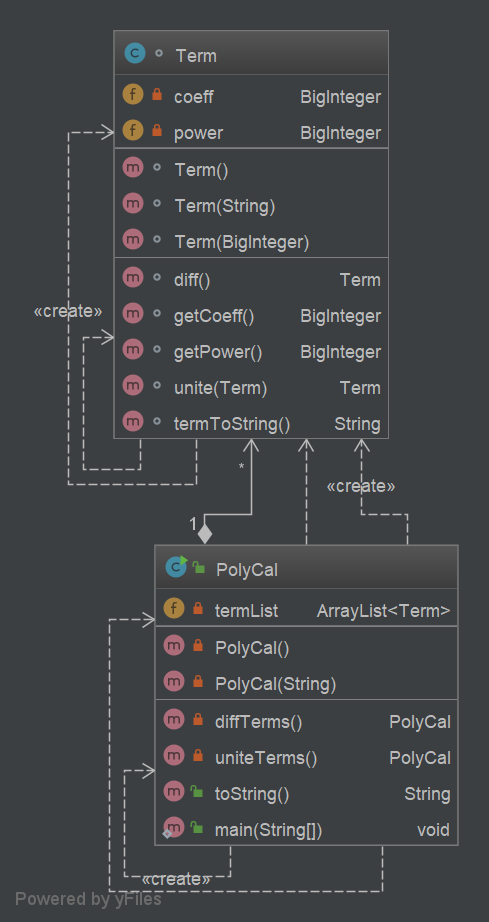
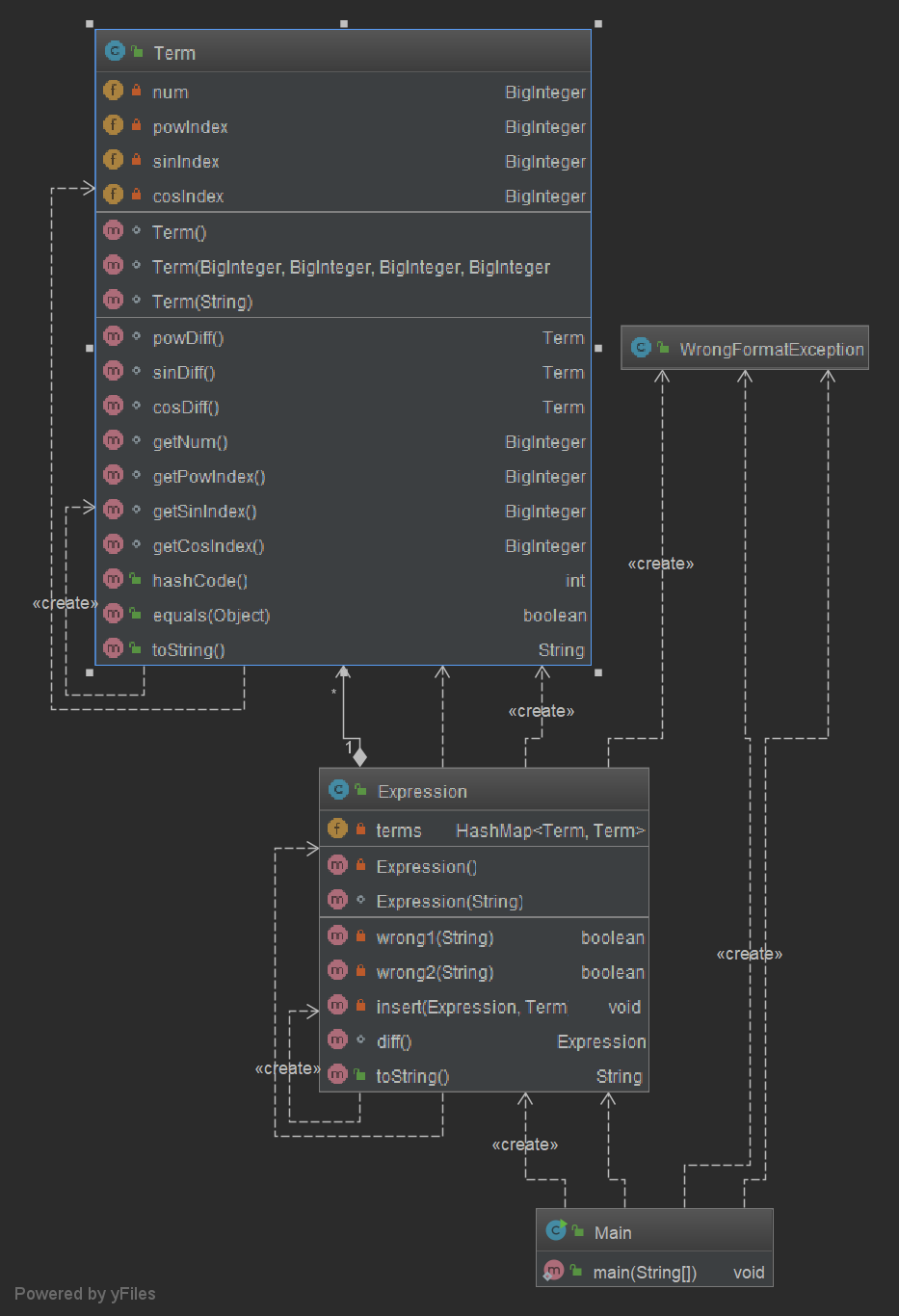
在这一次作业中,我划分了两个类,一个是PolyCal,一个是item,类图如左图所示。
程序入口main函数放在了PolyCal中,没有单独成类。字符串预处理放在main函数中进行。Term类主要实现了项字符串的解析(构造方法),项的求导,合并同类项,以及toString。PolyCal类采用ArrayList来管理表达式内的项,实现了表达式字符串的解析(构造方法),表达式求导,合并同类项,以及toString。
这次设计的不合理之处,一是没有把字符串预处理单拿出来写一个方法;再者合并同类项写的也不是很好,虽然能够完成作业,但是需要遍历数组元素,复杂度高,回过头来看使用hashmap应该会更好一些。再就是第一次作业中判断WF后没有使用异常。
度量与复杂度分析:
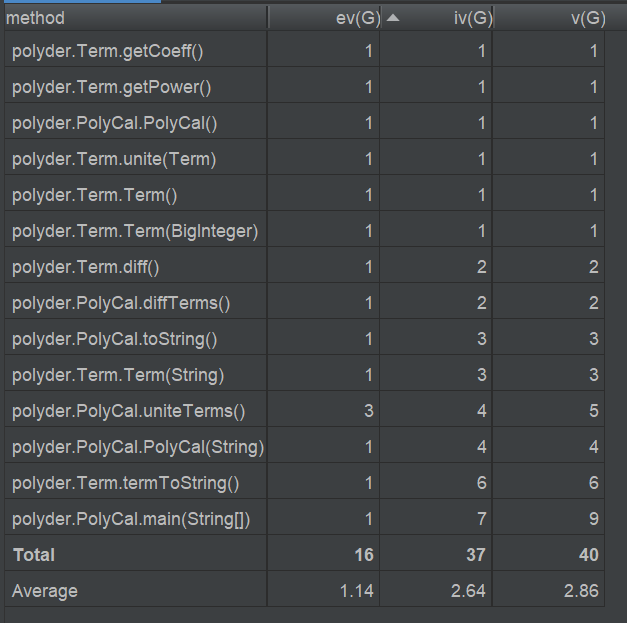
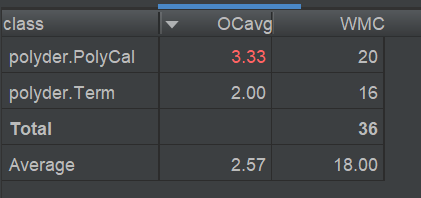
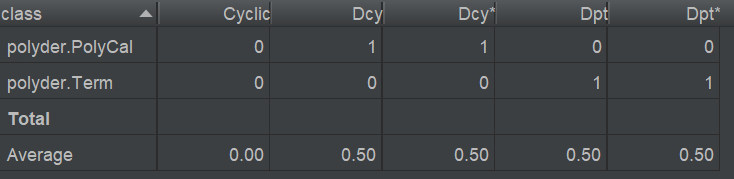
因为第一次作业不算复杂,因此大多数指标还好。PolyCal的OCavg(类的方法的平均循环复杂度)较高,分析代码后我认为,这主要合并同类项时的数组遍历以及解析表达式的构造方法对字符串的遍历导致的。
2.第二次作业
在第二次作业中,我们要完成包含简单幂函数和简单三角函数表达式的导函数的求解。相比于第一次作业,这次的作业中,因子可以是三角函数;因子连乘构成项。
在本次的作业中,我的程序主要还是两个类,Expression类和Term类。Expression类和第一次作业中的PolyCal类类似,Term类与第一次中的Poly类类似。有所不同的是,这一次的项类(即Term类)的成员变量是系数、幂函数的指数、正弦函数的指数、以及余弦函数的指数。这是考虑到,一个因子连乘构成的项,通过合并化简最后总能表示成 coeff * x^powIndex * sin(x)^sinIndex *cos(x)^cosIndex 这样四个因子相乘的形式。
这次作业一个很致命的问题就是,没有认真思考类之间的从属关系与关联关系,导致程序没有可扩展性,只能应付第二次作业,而第三次作业只能重头开始。
度量与复杂度分析

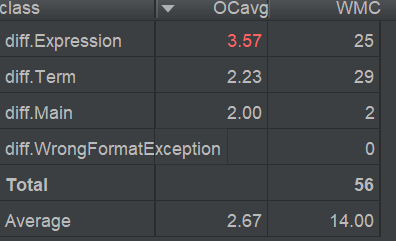
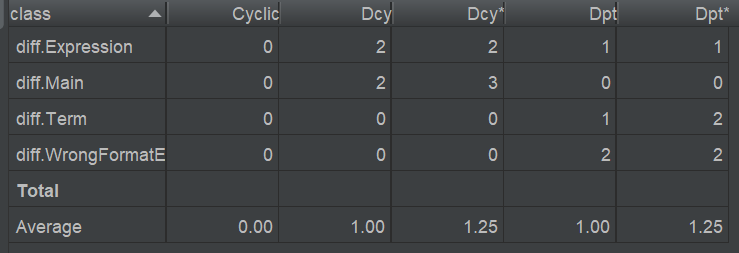
Expression类的OCavg较高的原因与第一次作业类似,不再赘述。其它问题,主要就是出在解析表达式字符串上,我前两次的作业在解析字符串时,是直接将正则匹配到的字符串作为构造函数的参数传入对应的构造函数的,这是导致问题的一个原因。另一个Wrong1方法超标是因为代码写的过丑。
3.第三次作业
第三次作业中在第二次的基础上,在因子中,新增了表达式因子,并且允许在三角函数中嵌套因子。
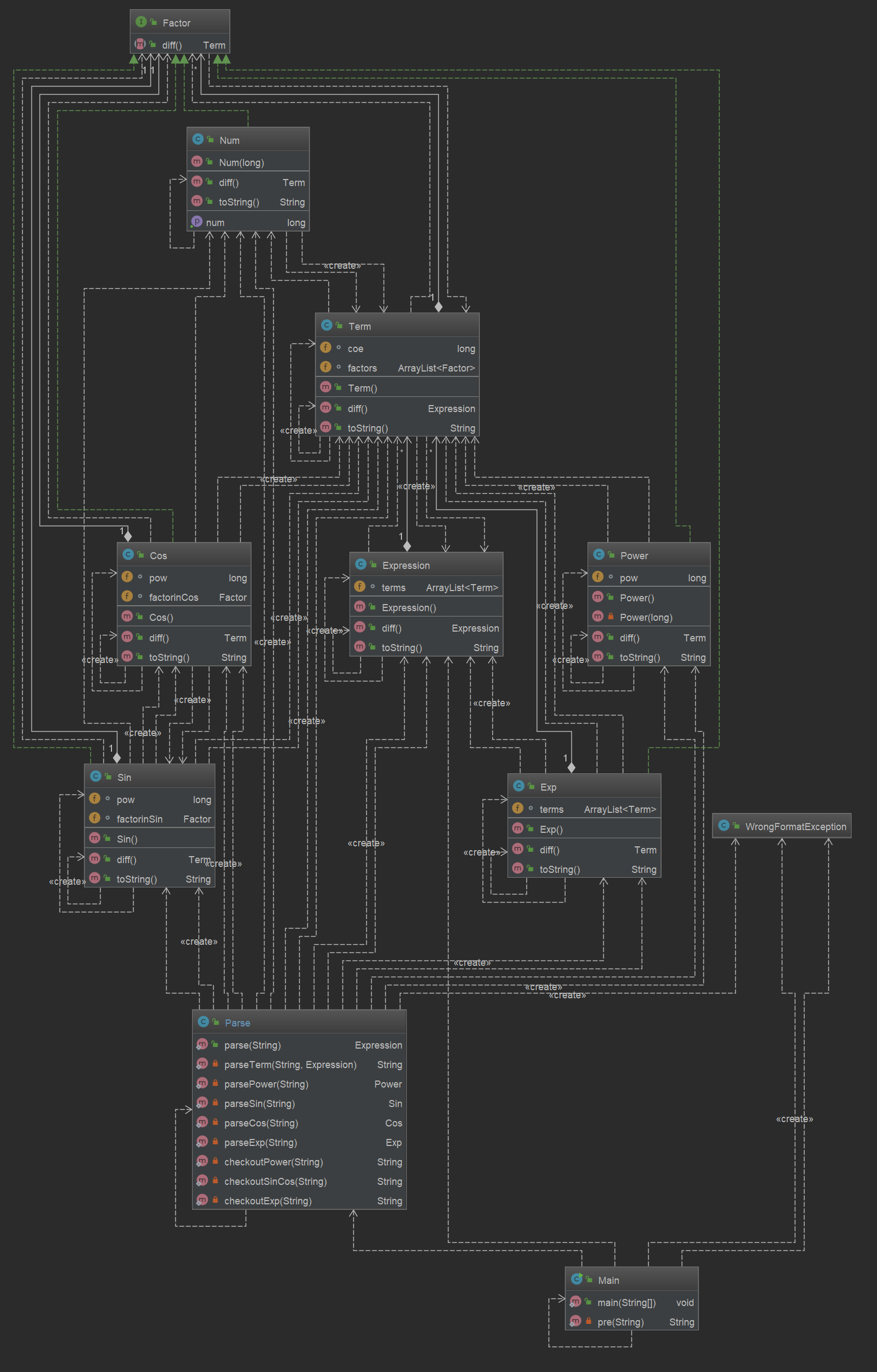
在本次作业中,大概划分了了Exp类、Term类,并实现了一个Factor接口。
在这次的作业中,困扰了我很久才解决的一个问题是输入的表达式字符串如何解析成表达式。在前两次的作业中,我都是利用正则表达式逐项解析表达式字符串。但是在第三次作业中,由于允许表达式因子和嵌套因子的出现,使用正则表达式解析项已经不太可能,最后选择了递归下降解析的写法。
在本次作业中,我认为最主要的一个问题,就是架构设计的还是有些不合理,主要体现在解析表达式的方法与整体架构设计的关系的处理上。另外本次作业没有进行优化,导致输出字符串的长度十分感人。
度量与复杂度分析
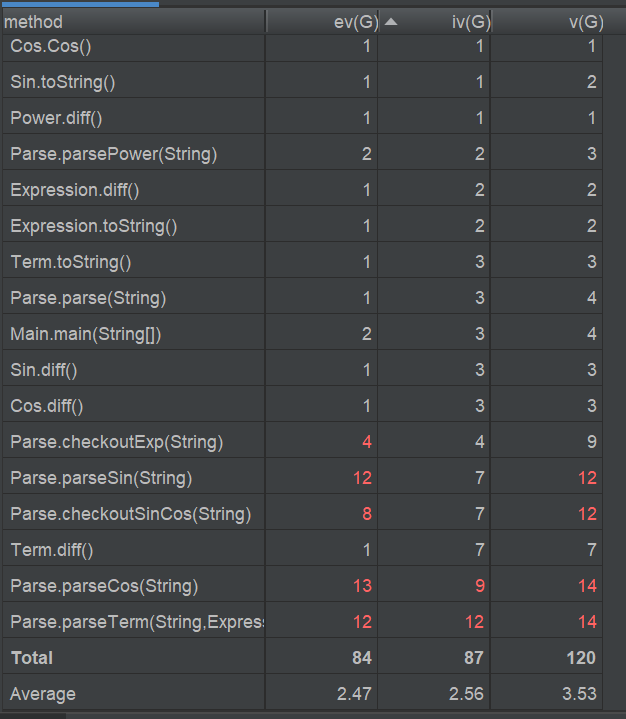
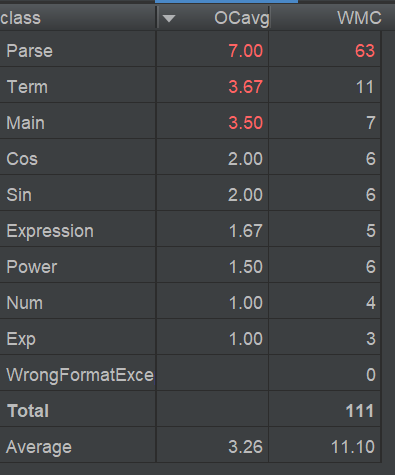
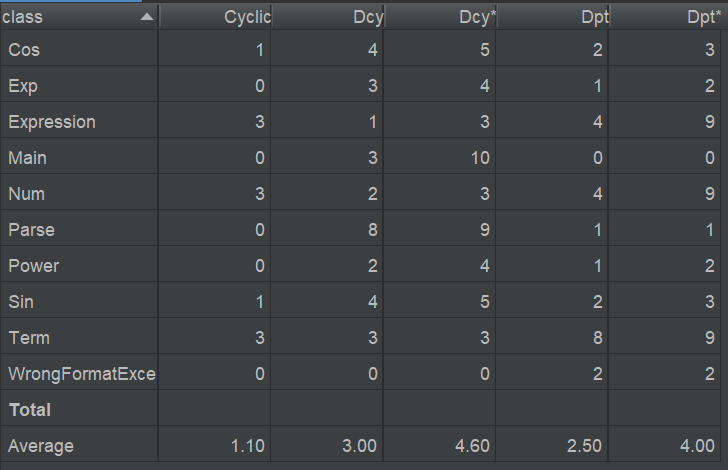
从这一次的复杂度分析结果来看,我的问题主要还是出在解析表达式字符串的方法中。因为架构设计不合理和解析字符串写的条理不够清楚,思路比较乱,Parse类的一些方法的指标超标严重。
- 二、自己作业中的bug分析
- 1. 预处理时考虑欠缺
在这三次作业中,我都先对读入的字符串进行了一些预处理,然后再解析字符串。
预处理的内容包括:1)判断有没有非法字符 2)判断有没有非法空格 3)判断结束之后删去所有的空白字符 4)对类似++ 、+-等合法的连续运算符进行处理,将其替换成一个单一的运算符。 在进行完4)的替换后,每一项前将存在仅存在一个+或-符号。 这之后我的思路是将表达式Exp看成若干项item的加和,而这些操作符被认为是其后面项的一部分(每一项的第一因子都是一个被简化的+1或-1)。之后依次解析每一项字符串。
在预处理之后,如果字符串还没被判为WF,那么经处理的字符串里将没有空白字符以及连续的 + -运算符。这样会简化之后解析字符串时的正则表达式的写法,这对我这种正则日常写出bug的人还是非常友好的。
bug出在预处理的4)上。在第一次作业中,我没有判断类似 +- 、++这样的连续操作符是不是合法的,就直接将字符串中两个连续操作符直接替换成了单个操作符。这样就导致类似 x^++2 的字符串,就会被错误的判定为是合法的字符串。针对该bug的修复,在处理连续+-字符串之前,先判断其是否合法即可。
- 2. 正则表达式写错。
因为自己某些地方手残写错了正则表达式,在第1,2,3次作业中都因此出现了bug。特此记录以警醒自己,写正则表达式的时候一定要小心谨慎。
- 3. 没有认真读参考书
自认为表达式中的自变量可以是x或X。
- 4. TLE错误。
这个错误出现在我的第三次作业中。原因是在解析表达式字符串的时候,对于有多重括号嵌套的因子,例如sin((((x)))) , ((((x^2))))等,我是逐层解析因子。这就意味着每多一层括号嵌套,就要调用一次解析表达式因子的方法。针对这个bug,在解析表达式的时候,遇到表达式因子,可以加一个判断是否其是不是多重括号嵌套的因子,是的话可以在解析表达式时简化这种因子为一个一重括号的表达式因子。
- 三、关于互测
在这几次互测我所用的数据包括:
1)自己在阅读指导书的要求、构思代码、debug时所想出的正确或错误样例,这几次互测表明这有一定的有效性,有些同学的确被卡在了我也掉进过的坑里。
2)阅读他人代码,分析其程序漏洞,构造测试数据。自我感觉这个方法不甚好,只针对测试而言,性价比有些低。(但是可以通过读别人的代码来学习到一些不同的思路和方法,这样来讲还蛮有用的。)这个方法我只在第一次作业中使用过,当时代码量还比较少,有耐心看一些别人的代码,但后两次就没有再用过了。
3)自己针对一些可能出错的点构造一些测试数据。感觉这也有些效果,第三次作业互测中体现的尤为明显,hack别人大部分靠的都是这样构造的数据。







