Differentiation
Def. Gradient f : X ⊆ R N → R f : X ⊆ R N → R differentiable . Then the gradient of f f x ∈ X x ∈ X ∇ f ( x ) ∇ f ( x )
∇ f ( x ) = ⎡ ⎢
⎢
⎢
⎢ ⎣ ∂ f ∂ x 1 ( x ) ⋮ ∂ f ∂ x N ( x ) ⎤ ⎥
⎥
⎥
⎥ ⎦ ∇ f ( x ) = [ ∂ f ∂ x 1 ( x ) ⋮ ∂ f ∂ x N ( x ) ]
Def. Hessian f : X ⊆ R N → R f : X ⊆ R N → R twice differentiable . Then the Hessian of f f x ∈ X x ∈ X ∇ 2 f ( x ) ∇ 2 f ( x )
∇ 2 f ( x ) = ⎡ ⎢
⎢
⎢
⎢
⎢
⎢ ⎣ ∂ 2 f ∂ x 2 1 ( x ) ⋯ ∂ 2 f ∂ x 1 , x N ( x ) ⋮ ⋱ ⋮ ∂ 2 f ∂ x N , x 1 ( x ) ⋯ ∂ 2 f ∂ x 2 N ( x ) ⎤ ⎥
⎥
⎥
⎥
⎥
⎥ ⎦ ∇ 2 f ( x ) = [ ∂ 2 f ∂ x 1 2 ( x ) ⋯ ∂ 2 f ∂ x 1 , x N ( x ) ⋮ ⋱ ⋮ ∂ 2 f ∂ x N , x 1 ( x ) ⋯ ∂ 2 f ∂ x N 2 ( x ) ]
Th. Fermat's theorem f : X ⊆ R N → R f : X ⊆ R N → R twice differentiable . If f f local extrememum at x ∗ x ∗ ∇ f ( x ∗ ) = 0 ∇ f ( x ∗ ) = 0
Convexity
Def. Convex set X ⊆ R N X ⊆ R N convex , if for any x , y ∈ X x , y ∈ X [ x , y ] [ x , y ] X X { α x + ( 1 − α ) y : 0 ≤ α ≤ 1 } ⊆ X { α x + ( 1 − α ) y : 0 ≤ α ≤ 1 } ⊆ X
Th. Operations that preserve convexity
C i C i i ∈ I i ∈ I ⋂ i ∈ I C i ⋂ i ∈ I C i C 1 , C 2 C 1 , C 2 C 1 + C 2 = { x 1 + x 2 : x 1 ∈ C 1 , x 2 ∈ X 2 } C 1 + C 2 = { x 1 + x 2 : x 1 ∈ C 1 , x 2 ∈ X 2 } C 1 , C 2 C 1 , C 2 C 1 × C 2 = { ( x 1 , x 2 ) : x 1 ∈ C 1 , x 2 ∈ X 2 } C 1 × C 2 = { ( x 1 , x 2 ) : x 1 ∈ C 1 , x 2 ∈ X 2 } Any projection of a convex set is also convex
Def. Convex hull Convex hull conv ( X ) conv ( X ) X ⊆ R N X ⊆ R N X X
conv ( X ) = { m ∑ i = 1 α i x i : ∀ ( x 1 , ⋯ , x m ) ∈ X , α i ≥ 0 , m ∑ i = 1 α i = 1 } conv ( X ) = { ∑ i = 1 m α i x i : ∀ ( x 1 , ⋯ , x m ) ∈ X , α i ≥ 0 , ∑ i = 1 m α i = 1 }
Def. Epigraph epigraph of f : X → R f : X → R Epi f Epi f { ( x , y ) : x ∈ X , y ≥ f ( x ) } { ( x , y ) : x ∈ X , y ≥ f ( x ) }
Def. Convex function X X f : X → R f : X → R convex , iff Epi f Epi f x , y ∈ X , α ∈ [ 0 , 1 ] x , y ∈ X , α ∈ [ 0 , 1 ]
f ( α x + ( 1 − α ) y ) ≤ α f ( x ) + ( 1 − α ) f ( y ) f ( α x + ( 1 − α ) y ) ≤ α f ( x ) + ( 1 − α ) f ( y )
Moreover, f f strictly convex if the inequality is strict when x ≠ y x ≠ y α ∈ ( 0 , 1 ) α ∈ ( 0 , 1 ) f f concave if − f − f
Th. Convex function characterized by first-order differential f : X ⊆ R N → R f : X ⊆ R N → R differentiable . Then f f dom ( f ) dom ( f )
∀ x , y ∈ dom ( f ) , f ( y ) − f ( x ) ≥ ∇ f ( x ) ⋅ ( y − x ) ∀ x , y ∈ dom ( f ) , f ( y ) − f ( x ) ≥ ∇ f ( x ) ⋅ ( y − x )
交换 x , y x , y f ( x ) − f ( y ) ≥ ∇ f ( y ) ⋅ ( x − y ) f ( x ) − f ( y ) ≥ ∇ f ( y ) ⋅ ( x − y )
⟨ ∇ f ( x ) − ∇ f ( y ) , x − y ⟩ ≥ 0 ⟨ ∇ f ( x ) − ∇ f ( y ) , x − y ⟩ ≥ 0
其含义为 “梯度单调且内积大等于零”,这也是凸性的等价条件之一
Th. Convex function characterized by second-order differential f : X ⊆ R N → R f : X ⊆ R N → R twice differentiable . Then f f dom ( f ) dom ( f ) Hessian is positive semidefinite (半正定)
∀ x ∈ dom ( f ) , ∇ 2 f ( x ) ⪰ 0 ∀ x ∈ dom ( f ) , ∇ 2 f ( x ) ⪰ 0
对称阵为半正定,若其所有特征值非负;A ⪰ B A ⪰ B A − B A − B
If f f x ↦ x 2 x ↦ x 2 f f ∀ x ∈ dom ( f ) , f ′′ ( x ) ≥ 0 ∀ x ∈ dom ( f ) , f ″ ( x ) ≥ 0
For example
Linear functions is both convex and concave
Any norm ∥ ⋅ ∥ ‖ ⋅ ‖ X X ∥ α x + ( 1 − α ) y ∥ ≤ ∥ α x ∥ + ∥ ( 1 − α ) y ∥ ≤ α ∥ x ∥ + ( 1 − α ) ∥ y ∥ ‖ α x + ( 1 − α ) y ‖ ≤ ‖ α x ‖ + ‖ ( 1 − α ) y ‖ ≤ α ‖ x ‖ + ( 1 − α ) ‖ y ‖
Using composition rules to prove convexity
Th. Composition of convex/concave functions h : R → R h : R → R g : R N → R g : R N → R f ( x ) = h ( g ( x ) ) , ∀ x ∈ R N f ( x ) = h ( g ( x ) ) , ∀ x ∈ R N
h h g g ⟹ ⟹ f f h h g g ⟹ ⟹ f f h h g g ⟹ ⟹ f f h h g g ⟹ ⟹ f f
Proof: It holds for N = 1 N = 1 g g ∥ ⋅ ∥ ‖ ⋅ ‖
Th. Pointwise maximum of convex functions f i f i C C i ∈ I i ∈ I f ( x ) = sup i ∈ I f i ( x ) , x ∈ C f ( x ) = sup i ∈ I f i ( x ) , x ∈ C Epi f = ⋂ i ∈ I Epi f i Epi f = ⋂ i ∈ I Epi f i
f ( x ) = max i ∈ I w i ⋅ x + b i f ( x ) = max i ∈ I w i ⋅ x + b i The maximum eigenvalue λ max ( M ) λ max ( M ) λ max ( M ) = sup ∥ x ∥ 2 ≤ 1 x ′ M x λ max ( M ) = sup ‖ x ‖ 2 ≤ 1 x ′ M x M ↦ x ′ M x M ↦ x ′ M x λ k ( M ) λ k ( M ) k k M ↦ ∑ k i = 1 λ i ( M ) M ↦ ∑ i = 1 k λ i ( M ) M ↦ ∑ n i = n − k + 1 λ i ( M ) = − ∑ k i = 1 λ i ( − M ) M ↦ ∑ i = n − k + 1 n λ i ( M ) = − ∑ i = 1 k λ i ( − M )
Th. Partial infimum f f C ⊆ X × Y C ⊆ X × Y B ⊆ Y B ⊆ Y A = { x ∈ X : ∃ y ∈ B , ( x , y ) ∈ C } A = { x ∈ X : ∃ y ∈ B , ( x , y ) ∈ C } g ( x ) = inf y ∈ B f ( x , y ) g ( x ) = inf y ∈ B f ( x , y ) x ∈ A x ∈ A B B d ( x ) = inf y ∈ B ∥ x − y ∥ d ( x ) = inf y ∈ B ‖ x − y ‖
Th. Jensen's inequality X X C ⊆ R N C ⊆ R N f f C C E [ X ] ∈ C , E [ f ( X ) ] E [ X ] ∈ C , E [ f ( X ) ]
f ( E [ X ] ) ≤ E [ f ( X ) ] f ( E [ X ] ) ≤ E [ f ( X ) ]
Sketch of proof: extending f ( ∑ α x ) ≤ ∑ α f ( x ) f ( ∑ α x ) ≤ ∑ α f ( x ) ∑ α = 1 ∑ α = 1
Smoothness, strong convexity
参考 [https://zhuanlan.zhihu.com/p/619288199 ]
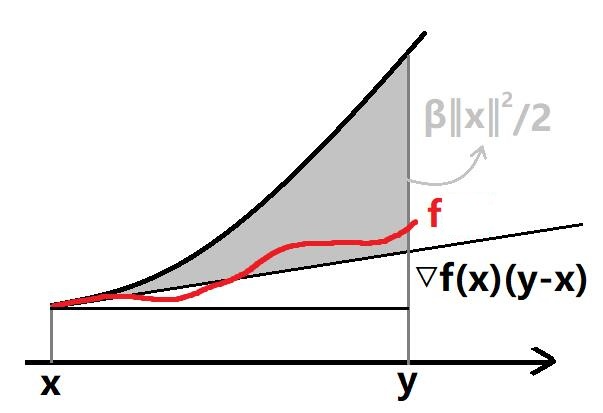
Def. β β f f β β
∀ x , y ∈ dom ( f ) , ∥ ∇ f ( x ) − ∇ f ( y ) ∥ ≤ β ∥ x − y ∥ ∀ x , y ∈ dom ( f ) , ‖ ∇ f ( x ) − ∇ f ( y ) ‖ ≤ β ‖ x − y ‖
等价于如下命题均成立:
β 2 ∥ x ∥ 2 − f ( x ) β 2 ‖ x ‖ 2 − f ( x ) ∀ x , y ∈ dom ( f ) , f ( y ) ≤ f ( x ) + ∇ f ( x ) ⊤ ( y − x ) + β 2 ∥ y − x ∥ 2 ∀ x , y ∈ dom ( f ) , f ( y ) ≤ f ( x ) + ∇ f ( x ) ⊤ ( y − x ) + β 2 ‖ y − x ‖ 2 ∇ 2 f ( x ) ⪯ β I ∇ 2 f ( x ) ⪯ β I
证明/说明g ( x ) = β 2 ∥ x ∥ 2 − f ( x ) g ( x ) = β 2 ‖ x ‖ 2 − f ( x ) ⟨ ∇ g ( x ) − ∇ g ( y ) , x − y ⟩ ≥ 0 ⟨ ∇ g ( x ) − ∇ g ( y ) , x − y ⟩ ≥ 0 f f β 2 ∥ x ∥ 2 β 2 ‖ x ‖ 2 f f g ( y ) − g ( x ) ≥ ∇ g ( x ) ⋅ ( y − x ) g ( y ) − g ( x ) ≥ ∇ g ( x ) ⋅ ( y − x ) ∇ 2 g ( x ) ⪰ 0 ∇ 2 g ( x ) ⪰ 0
Def. α α f f α α
∀ x , y ∈ dom ( f ) , ∥ ∇ f ( x ) − ∇ f ( y ) ∥ ≥ α ∥ x − y ∥ ∀ x , y ∈ dom ( f ) , ‖ ∇ f ( x ) − ∇ f ( y ) ‖ ≥ α ‖ x − y ‖ f ( x ) − α 2 ∥ x ∥ 2 f ( x ) − α 2 ‖ x ‖ 2 ∀ x , y ∈ dom ( f ) , f ( y ) ≥ f ( x ) + ∇ f ( x ) ⊤ ( y − x ) + α 2 ∥ y − x ∥ 2 ∀ x , y ∈ dom ( f ) , f ( y ) ≥ f ( x ) + ∇ f ( x ) ⊤ ( y − x ) + α 2 ‖ y − x ‖ 2 ∇ 2 f ( x ) ⪰ α I ∇ 2 f ( x ) ⪰ α I
Def. γ γ f f γ γ α α β β f f condition number 为 γ = α / β ≤ 1 γ = α / β ≤ 1
Th. Linear combination of two convex functions
考虑两个凸函数的加和,有:
若 f f α 1 α 1 g g α 2 α 2 f + g f + g ( α 1 + α 2 ) ( α 1 + α 2 )
若 f f β 1 β 1 g g β 2 β 2 f + g f + g ( β 1 + β 2 ) ( β 1 + β 2 )
考虑凸函数的数乘 k > 0 k > 0
若 f f α α k f k f ( k α ) ( k α )
若 f f β β k f k f ( k β ) ( k β )
证明,利用凸函数满足 ⟨ ∇ f ( x ) − ∇ f ( y ) , x − y ⟩ ≥ 0 ⟨ ∇ f ( x ) − ∇ f ( y ) , x − y ⟩ ≥ 0 β 2 ∥ x ∥ 2 − f ( x ) , f ( x ) − α 2 ∥ x ∥ 2 β 2 ‖ x ‖ 2 − f ( x ) , f ( x ) − α 2 ‖ x ‖ 2
Projections onto convex sets
之后的算法会涉及向凸集投影的概念;定义 y y K K
∏ K ( y ) ≜ arg min x ∈ K ∥ x − y ∥ ∏ K ( y ) ≜ arg min x ∈ K ‖ x − y ‖
可以证明投影总是唯一的;投影还具有一个很重要的性质:Th. Pythagorean theorem 勾股定理 K ⊆ R d , y ∈ R d , x = ∏ K ( y ) K ⊆ R d , y ∈ R d , x = ∏ K ( y ) z ∈ K z ∈ K ∥ y − z ∥ ≥ ∥ x − z ∥ ‖ y − z ‖ ≥ ‖ x − z ‖
Constrained optimization 带约束优化
Def. Constrained optimization problem X ⊆ R N , f , g i : X → R , i ∈ [ m ] X ⊆ R N , f , g i : X → R , i ∈ [ m ] primal problem )的形式为
min x ∈ X f ( x ) s u b j e c t t o : g i ( x ) ≤ 0 , ∀ i ∈ [ m ] min x ∈ X f ( x ) s u b j e c t t o : g i ( x ) ≤ 0 , ∀ i ∈ [ m ]
记 inf x ∈ X f ( x ) = p ∗ inf x ∈ X f ( x ) = p ∗ g = 0 g = 0 g ≤ 0 , − g ≤ 0 g ≤ 0 , − g ≤ 0
Dual problem and saddle point 解决这类问题,可以先引入拉格朗日函数 Lagrange function ,将约束以非正项引入;然后转化成对偶问题
Def. Lagrange function
∀ x ∈ X , ∀ α ≥ 0 , L ( x , α ) = f ( x ) + m ∑ i = 1 α i g i ( x ) ∀ x ∈ X , ∀ α ≥ 0 , L ( x , α ) = f ( x ) + ∑ i = 1 m α i g i ( x )
其中 α = ( α 1 , ⋯ , α m ) ′ α = ( α 1 , ⋯ , α m ) ′ dual variable g = 0 g = 0 α = α + − α − α = α + − α − g , − g g , − g g g w ⋅ x + b w ⋅ x + b p ∗ = inf x sup α L ( x , α ) p ∗ = inf x sup α L ( x , α ) x x sup α sup α
Def. Dual function
∀ α ≥ 0 , F ( α ) = inf x ∈ X L ( x , α ) = inf x ∈ X ( f ( x ) + m ∑ i = 1 α i g i ( x ) ) ∀ α ≥ 0 , F ( α ) = inf x ∈ X L ( x , α ) = inf x ∈ X ( f ( x ) + ∑ i = 1 m α i g i ( x ) )
它是 concave 的,因为 L L α α α α F ( α ) ≤ inf x ∈ X f ( x ) = p ∗ F ( α ) ≤ inf x ∈ X f ( x ) = p ∗
Def. Dual problem
max α F ( α ) s u b j e c t t o : α ≥ 0 max α F ( α ) s u b j e c t t o : α ≥ 0
对偶问题是凸优化问题,即求 concave 函数的最大值,记其为 d ∗ d ∗ d ∗ ≤ p ∗ d ∗ ≤ p ∗
d ∗ = sup α inf x L ( x , α ) ≤ inf x sup α L ( x , α ) = p ∗ d ∗ = sup α inf x L ( x , α ) ≤ inf x sup α L ( x , α ) = p ∗
称为弱对偶 weak duality ,取等情况称为强对偶 strong duality
当凸优化问题 满足约束规范性条件 constraint qualification (Slater's contidion) 时(此为充分条件),有 d ∗ = p ∗ d ∗ = p ∗ saddle point
Def. Constraint qualification (Slater's condition) X X int ( X ) ≠ ∅ int ( X ) ≠ ∅
定义 strong constraint qualification (Slater's condition) 为
∃ ¯ x ∈ int ( X ) : ∀ i ∈ [ m ] , g i ( ¯ x ) < 0 ∃ x ¯ ∈ int ( X ) : ∀ i ∈ [ m ] , g i ( x ¯ ) < 0
定义 weak constraint qualification (weak Slater's condition) 为
∃ ¯ x ∈ int ( X ) : ∀ i ∈ [ m ] , ( g i ( ¯ x ) < 0 ) ∨ ( g i ( ¯ x ) = 0 ∧ g i affine ) ∃ x ¯ ∈ int ( X ) : ∀ i ∈ [ m ] , ( g i ( x ¯ ) < 0 ) ∨ ( g i ( x ¯ ) = 0 ∧ g i affine )
(这个条件是在说明解存在吗?)saddle point 是带约束优化问题的解的充要条件
Th. Saddle point - sufficient condition saddle point ( x ∗ , α ∗ ) ( x ∗ , α ∗ )
∀ x ∈ X , ∀ α ≥ 0 , L ( x ∗ , α ) ≤ L ( x ∗ , α ∗ ) ≤ L ( x , α ∗ ) ∀ x ∈ X , ∀ α ≥ 0 , L ( x ∗ , α ) ≤ L ( x ∗ , α ∗ ) ≤ L ( x , α ∗ )
则 x ∗ x ∗ f ( x ∗ ) = inf f ( x ) f ( x ∗ ) = inf f ( x )
Th. Saddle point - necessary condition f , g i , i ∈ [ m ] f , g i , i ∈ [ m ] convex function :
若满足 Slater's condition ,则带约束优化问题的解 x ∗ x ∗ α ∗ ≥ 0 α ∗ ≥ 0 ( x ∗ , α ∗ ) ( x ∗ , α ∗ )
若满足 weak Slater's condition 且 f , g i f , g i 可导 ,则带约束优化问题的解 x ∗ x ∗ α ∗ ≥ 0 α ∗ ≥ 0 ( x ∗ , α ∗ ) ( x ∗ , α ∗ )
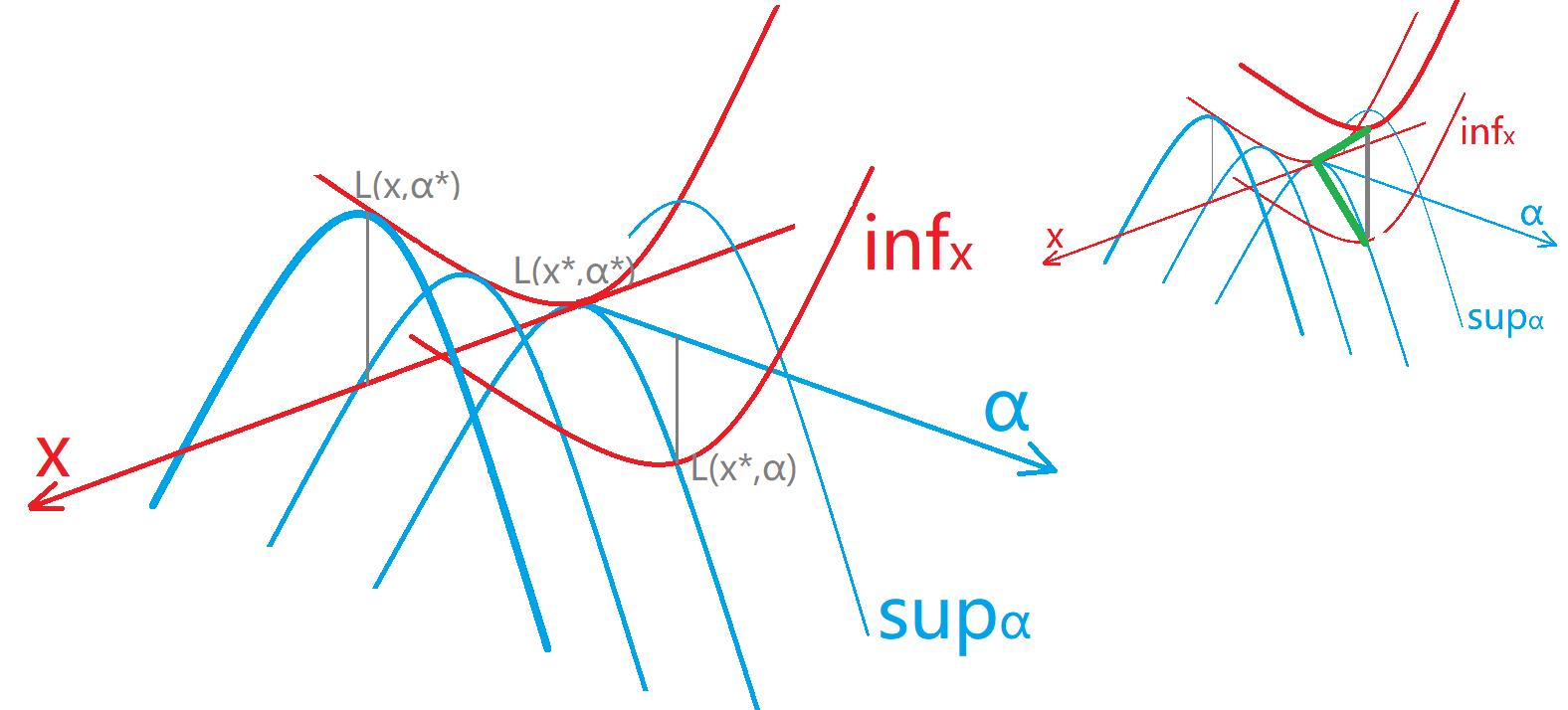
由于书本上没提供必要性的证明,且充分性证明不难但是不够漂亮,所以就不抄了,只给出我自己的思路(虽然可能有缺陷,下图也只是示意):
d ∗ = sup α inf x L ( x , α ) ≤ inf x sup α L ( x , α ) = p ∗ d ∗ = sup α inf x L ( x , α ) ≤ inf x sup α L ( x , α ) = p ∗
定义 x ∗ x ∗ p ∗ = sup α L ( x ∗ , α ) ≤ sup α L ( x , α ) , ∀ x p ∗ = sup α L ( x ∗ , α ) ≤ sup α L ( x , α ) , ∀ x α ∗ α ∗ d ∗ = inf x L ( x , α ∗ ) ≥ inf x L ( x , α ) , ∀ α d ∗ = inf x L ( x , α ∗ ) ≥ inf x L ( x , α ) , ∀ α
L L ( x ∗ , α ∗ ) ( x ∗ , α ∗ ) p ∗ = d ∗ p ∗ = d ∗ p ∗ = d ∗ = L ( x ∗ , α ∗ ) p ∗ = d ∗ = L ( x ∗ , α ∗ )
分别记为命题 A , B , C , D A , B , C , D B → A , D → C B → A , D → C
证明 A → B , B → C D A → B , B → C D ( x ′ , α ′ ) ( x ′ , α ′ ) L ( x ′ , α ∗ ) ≤ L ( x ′ , α ′ ) = inf x L ( x , α ′ ) ≤ inf x L ( x , α ∗ ) L ( x ′ , α ∗ ) ≤ L ( x ′ , α ′ ) = inf x L ( x , α ′ ) ≤ inf x L ( x , α ∗ ) inf x L ( x , α ∗ ) ≤ L ( x ′ , α ∗ ) = inf x L ( x , α ′ ) inf x L ( x , α ∗ ) ≤ L ( x ′ , α ∗ ) = inf x L ( x , α ′ ) α ∗ α ∗ α ∗ ← α ′ α ∗ ← α ′ x ∗ , x ′ x ∗ , x ′ ( x ∗ , α ∗ ) ( x ∗ , α ∗ ) ∀ x , ∀ α , L ( x ∗ , α ) ≤ L ( x ∗ , α ∗ ) ≤ L ( x , α ∗ ) ∀ x , ∀ α , L ( x ∗ , α ) ≤ L ( x ∗ , α ∗ ) ≤ L ( x , α ∗ ) p ∗ = sup α L ( x ∗ , α ) = L ( x ∗ , α ∗ ) = inf x L ( x , α ∗ ) = d ∗ p ∗ = sup α L ( x ∗ , α ) = L ( x ∗ , α ∗ ) = inf x L ( x , α ∗ ) = d ∗
证明 C → B D C → B D p ∗ = d ∗ p ∗ = d ∗ sup α L ( x ∗ , α ) = inf x L ( x , α ∗ ) sup α L ( x ∗ , α ) = inf x L ( x , α ∗ ) sup α L ( x ∗ , α ) ≥ L ( x ∗ , α ∗ ) ≥ inf x L ( x , α ∗ ) sup α L ( x ∗ , α ) ≥ L ( x ∗ , α ∗ ) ≥ inf x L ( x , α ∗ ) ∀ x , ∀ α , L ( x ∗ , α ) ≤ sup α L ( x ∗ , α ) = L ( x ∗ , α ∗ ) = inf x L ( x , α ∗ ) ≤ L ( x , α ∗ ) ∀ x , ∀ α , L ( x ∗ , α ) ≤ sup α L ( x ∗ , α ) = L ( x ∗ , α ∗ ) = inf x L ( x , α ∗ ) ≤ L ( x , α ∗ ) ( x ∗ , α ∗ ) ( x ∗ , α ∗ )
综上得证。爽!
KKT conditions Lagrangian version 若带约束优化问题满足 convexity,我们就可以用一个定理解决:KKT
Th. Karush-Kuhn-Tucker's theorem f , g i : X → R , ∀ i ∈ [ m ] f , g i : X → R , ∀ i ∈ [ m ] convex and differentiable Slater's condition ;则带约束优化问题
min x ∈ X , g ( x ) ≤ 0 f ( x ) min x ∈ X , g ( x ) ≤ 0 f ( x )
其拉格朗日函数为 L ( x , α ) = f ( x ) + α ⋅ g ( x ) , α ≥ 0 L ( x , α ) = f ( x ) + α ⋅ g ( x ) , α ≥ 0 ¯ x x ¯ ¯ α ≥ 0 α ¯ ≥ 0
∇ x L ( ¯ x , ¯ α ) = ∇ x f ( ¯ x ) + ¯ α ⋅ ∇ x g ( ¯ x ) = 0 ∇ α L ( ¯ x , ¯ α ) = g ( ¯ x ) ≤ 0 ¯ α ⋅ g ( ¯ x ) = 0 ; KKT conditions ∇ x L ( x ¯ , α ¯ ) = ∇ x f ( x ¯ ) + α ¯ ⋅ ∇ x g ( x ¯ ) = 0 ∇ α L ( x ¯ , α ¯ ) = g ( x ¯ ) ≤ 0 α ¯ ⋅ g ( x ¯ ) = 0 ; KKT conditions
其中后两条称为互补条件 complementarity conditions ,即对任意 i ∈ [ m ] , ¯ α i ≥ 0 , g i ( ¯ x ) ≤ 0 i ∈ [ m ] , α ¯ i ≥ 0 , g i ( x ¯ ) ≤ 0 ¯ α i g i ( ¯ x ) = 0 α ¯ i g i ( x ¯ ) = 0
充要性证明:
必要性,¯ x x ¯ ¯ α α ¯ ( ¯ x , ¯ α ) ( x ¯ , α ¯ )
∀ α , L ( ¯ x , α ) ≤ L ( ¯ x , ¯ α ) ⟹ α ⋅ g ( ¯ x ) ≤ ¯ α ⋅ g ( ¯ x ) α → + ∞ ⟹ g ( ¯ x ) ≤ 0 α → 0 ⟹ ¯ α ⋅ g ( ¯ x ) = 0 ∀ α , L ( x ¯ , α ) ≤ L ( x ¯ , α ¯ ) ⟹ α ⋅ g ( x ¯ ) ≤ α ¯ ⋅ g ( x ¯ ) α → + ∞ ⟹ g ( x ¯ ) ≤ 0 α → 0 ⟹ α ¯ ⋅ g ( x ¯ ) = 0
充分性,满足 KKT 条件,则对于满足 g ( x ) ≤ 0 g ( x ) ≤ 0 x x
f ( x ) − f ( ¯ x ) ≥ ∇ x f ( ¯ x ) ⋅ ( x − ¯ x ) ; convexity of f = − ¯ α ⋅ ∇ x g ( ¯ x ) ⋅ ( x − ¯ x ) ; first cond ≥ − ¯ α ⋅ ( g ( x ) − g ( ¯ x ) ) ; convexity of g = − ¯ α ⋅ g ( x ) ≥ 0 ; third cond f ( x ) − f ( x ¯ ) ≥ ∇ x f ( x ¯ ) ⋅ ( x − x ¯ ) ; convexity of f = − α ¯ ⋅ ∇ x g ( x ¯ ) ⋅ ( x − x ¯ ) ; first cond ≥ − α ¯ ⋅ ( g ( x ) − g ( x ¯ ) ) ; convexity of g = − α ¯ ⋅ g ( x ) ≥ 0 ; third cond
Gradient descent version 我们还能用另一种思路阐述 KKT 定理,并且也是另一种求解带约束优化问题的方法:梯度下降g g K = { x : g ( x ) ≤ 0 } K = { x : g ( x ) ≤ 0 } K K
Th. Karush-Kuhn-Tucker's theorem, gradient descent version f f convex and differentiable K K
min x ∈ K f ( x ) min x ∈ K f ( x )
则 x ∗ x ∗
∀ y ∈ K , − ∇ f ( x ∗ ) ⊤ ( y − x ∗ ) ≤ 0 ∀ y ∈ K , − ∇ f ( x ∗ ) ⊤ ( y − x ∗ ) ≤ 0
其思想为,负梯度方向为 f f y − x ∗ y − x ∗ x ∗ x ∗
Gradient descent Unconstrained case 无约束凸优化问题的梯度下降 GD 算法∇ t = ∇ f ( x t ) , h t = f ( x t ) − f ( x ∗ ) , d t = ∥ x t − x ∗ ∥ ∇ t = ∇ f ( x t ) , h t = f ( x t ) − f ( x ∗ ) , d t = ‖ x t − x ∗ ‖
Algorithm. Gradient descent – –––––––––––––––––––––––––––––––––––––––––––––––––––––– – Input T , x 0 , { η t } for t = 0 , ⋯ , T − 1 do x t + 1 = x t − η t ∇ t end for return ¯ x = argmin x t { f ( x t ) } Algorithm. Gradient descent _ Input T , x 0 , { η t } for t = 0 , ⋯ , T − 1 do x t + 1 = x t − η t ∇ t end for return x ¯ = argmin x t { f ( x t ) }
其中合理地选择 η t η t Polyak stepsize :η t = h t ∥ ∇ t ∥ 2 η t = h t ‖ ∇ t ‖ 2
Th. Bound for GD with Polyak stepsize ∥ ∇ t ∥ ≤ G ‖ ∇ t ‖ ≤ G
f ( ¯ x ) − f ( x ∗ ) = min 0 ≤ t ≤ T { h t } ≤ min { G d 0 √ T , 2 β d 2 0 T , 3 G 2 α T , β d 2 0 ( 1 − γ 4 ) T } f ( x ¯ ) − f ( x ∗ ) = min 0 ≤ t ≤ T { h t } ≤ min { G d 0 T , 2 β d 0 2 T , 3 G 2 α T , β d 0 2 ( 1 − γ 4 ) T }
该定理的证明建立在 d 2 t + 1 ≤ d 2 t − h 2 t / ∥ ∇ t ∥ 2 d t + 1 2 ≤ d t 2 − h t 2 / ‖ ∇ t ‖ 2 h t = f ( x t ) − f ( x ∗ ) h t = f ( x t ) − f ( x ∗ ) h t + 1 − h t h t + 1 − h t ∥ ∇ t ∥ ‖ ∇ t ‖ d t = ∥ x − x ∗ ∥ d t = ‖ x − x ∗ ‖ d t + 1 − d t d t + 1 − d t
α 2 d 2 t ≤ h t ≤ β 2 d 2 t 1 2 β ∥ ∇ t ∥ 2 ≤ h t ≤ 1 2 α ∥ ∇ t ∥ 2 α 2 d t 2 ≤ h t ≤ β 2 d t 2 1 2 β ‖ ∇ t ‖ 2 ≤ h t ≤ 1 2 α ‖ ∇ t ‖ 2
对于更新式 x t + 1 = x t − η t ∇ t x t + 1 = x t − η t ∇ t d t + 1 − d t d t + 1 − d t x ∗ x ∗ d 2 t + 1 ≤ d 2 t − h 2 t / ∥ ∇ t ∥ 2 d t + 1 2 ≤ d t 2 − h t 2 / ‖ ∇ t ‖ 2 f ( ¯ x ) − f ( x ∗ ) ≤ 1 T ∑ t h t f ( x ¯ ) − f ( x ∗ ) ≤ 1 T ∑ t h t h t + 1 − h t h t + 1 − h t
h t + 1 − h t = f ( x t + 1 ) − f ( x t ) ≤ ∇ f ( x t ) ⊤ ( x t + 1 − x t ) + β 2 ∥ x t + 1 − x t ∥ 2 = − η t ∥ ∇ t ∥ 2 + β 2 η 2 t ∥ ∇ t ∥ 2 = − 1 2 β ∥ ∇ t ∥ 2 ; 令 η t = 1 β ≤ − α β h t = − γ h t h t + 1 − h t = f ( x t + 1 ) − f ( x t ) ≤ ∇ f ( x t ) ⊤ ( x t + 1 − x t ) + β 2 ‖ x t + 1 − x t ‖ 2 = − η t ‖ ∇ t ‖ 2 + β 2 η t 2 ‖ ∇ t ‖ 2 = − 1 2 β ‖ ∇ t ‖ 2 ; 令 η t = 1 β ≤ − α β h t = − γ h t
于是 h T ≤ ( 1 − γ ) h T − 1 ≤ ( 1 − γ ) T h 0 ≤ e − γ T h 0 h T ≤ ( 1 − γ ) h T − 1 ≤ ( 1 − γ ) T h 0 ≤ e − γ T h 0
Th. Bound for GD, unconstrained case f f γ γ η t = 1 β η t = 1 β
h T ≤ e − γ T h 0 h T ≤ e − γ T h 0
Constrained case 带约束优化的梯度下降,只需要每次移动后,投影到凸集
Algorithm. Basic gradient descent – –––––––––––––––––––––––––––––––––––––––––––––––––––––––––––– – Input T , x 0 ∈ K , { η t } for t = 0 , ⋯ , T − 1 do x t + 1 = Π K ( x t − η t ∇ t ) end for return ¯ x = argmin x t { f ( x t ) } Algorithm. Basic gradient descent _ Input T , x 0 ∈ K , { η t } for t = 0 , ⋯ , T − 1 do x t + 1 = Π K ( x t − η t ∇ t ) end for return x ¯ = argmin x t { f ( x t ) }
它有个类似的上限:Th. Bound for GD, constrained case f f γ γ η t = 1 β η t = 1 β
h T ≤ e − γ T / 4 h 0 h T ≤ e − γ T / 4 h 0
证明
x t + 1 = Π K ( x t − η t ∇ t ) = argmin x ∥ x − x t + η t ∇ t ∥ = argmin x ( ∇ ⊤ t ( x − x t ) + 1 2 η t ∥ x − x t ∥ 2 ) x t + 1 = Π K ( x t − η t ∇ t ) = argmin x ‖ x − x t + η t ∇ t ‖ = argmin x ( ∇ t ⊤ ( x − x t ) + 1 2 η t ‖ x − x t ‖ 2 )
根据如下式子,可以令 η t = 1 β η t = 1 β
h t + 1 − h t = f ( x t + 1 ) − f ( x t ) ≤ ∇ ⊤ t ( x t + 1 − x t ) + β 2 ∥ x t + 1 − x t ∥ 2 = min x ( ∇ ⊤ t ( x − x t ) + β 2 ∥ x − x t ∥ 2 ) h t + 1 − h t = f ( x t + 1 ) − f ( x t ) ≤ ∇ t ⊤ ( x t + 1 − x t ) + β 2 ‖ x t + 1 − x t ‖ 2 = min x ( ∇ t ⊤ ( x − x t ) + β 2 ‖ x − x t ‖ 2 )
为了摘掉 min min ,我们可以代入某个 x x ,代入哪个呢?可以考虑两点的连线,即 ( 1 − μ ) x t + μ x ∗ ( 1 − μ ) x t + μ x ∗
h t + 1 − h t ≤ min x ∈ [ x t , x ∗ ] ( ∇ ⊤ t ( x − x t ) + β 2 ∥ x − x t ∥ 2 ) ≤ μ ∇ ⊤ t ( x ∗ − x t ) + μ 2 β 2 ∥ x ∗ − x t ∥ 2 ≤ − μ h t + μ 2 β − α 2 ∥ x ∗ − x t ∥ 2 ; α -strong convex ≤ − μ h t + μ 2 β − α α h t ; Lemma h t + 1 − h t ≤ min x ∈ [ x t , x ∗ ] ( ∇ t ⊤ ( x − x t ) + β 2 ‖ x − x t ‖ 2 ) ≤ μ ∇ t ⊤ ( x ∗ − x t ) + μ 2 β 2 ‖ x ∗ − x t ‖ 2 ≤ − μ h t + μ 2 β − α 2 ‖ x ∗ − x t ‖ 2 ; α -strong convex ≤ − μ h t + μ 2 β − α α h t ; Lemma
对 μ ∈ [ 0 , 1 ] μ ∈ [ 0 , 1 ]
h t + 1 ≤ h t ( 1 − α 4 ( β − α ) ) ≤ h t ( 1 − γ 4 ) ≤ h t e − γ / 4 h t + 1 ≤ h t ( 1 − α 4 ( β − α ) ) ≤ h t ( 1 − γ 4 ) ≤ h t e − γ / 4
从而得证
GD: Reductions to non-smooth and non-strongly convex functions 现在来考虑梯度下降对不一定 smooth、或不一定 strong convex 的凸函数时该怎么分析;下文提到的 reduction 方法可以导出近似最优的收敛速度,而且很简单、很普适
Case 1. reduction to smooth, non-strongly convex functions 考虑仅有 β β 0 0
Algorithm. Gradient descent, reduction to β -smooth functions – –––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––– – Input f , T , x 0 ∈ K , parameter ~ α Let g ( x ) = f ( x ) + ~ α 2 ∥ x − x 0 ∥ 2 Apply GD on g , T , { η t = 1 β } , x 0 Algorithm. Gradient descent, reduction to β -smooth functions _ Input f , T , x 0 ∈ K , parameter α ~ Let g ( x ) = f ( x ) + α ~ 2 ‖ x − x 0 ‖ 2 Apply GD on g , T , { η t = 1 β } , x 0
取 ~ α = β log T D 2 T α ~ = β log T D 2 T h T = O ( β log T T ) h T = O ( β log T T ) O ( β / T ) O ( β / T )
由于 f f β β 0 0 ~ α α ~ ~ α α ~ ∥ x − x 0 ∥ 2 ‖ x − x 0 ‖ 2 g g ( β + ~ α ) ( β + α ~ ) ~ α α ~ f f
h t = f ( x t ) − f ( x ∗ ) = g ( x t ) − g ( x ∗ ) + ~ α 2 ( ∥ x ∗ − x 0 ∥ 2 − ∥ x t − x 0 ∥ 2 ) ≤ h g 0 exp − ~ α t / 4 ( ~ α + β ) + ~ α D 2 ; D is diameter of bounded K = O ( β log t t ) ; choosing ~ α = β log t D 2 t , ignore some constants h t = f ( x t ) − f ( x ∗ ) = g ( x t ) − g ( x ∗ ) + α ~ 2 ( ‖ x ∗ − x 0 ‖ 2 − ‖ x t − x 0 ‖ 2 ) ≤ h 0 g exp − α ~ t / 4 ( α ~ + β ) + α ~ D 2 ; D is diameter of bounded K = O ( β log t t ) ; choosing α ~ = β log t D 2 t , ignore some constants
Case 2. reduction to strongly convex, non-smooth functions 考虑仅有 α α f f ^ f δ : R d → R f ^ δ : R d → R B = { v : ∥ v ∥ ≤ 1 } B = { v : ‖ v ‖ ≤ 1 } δ δ
^ f δ ( x ) = E v ∼ U ( B ) [ f ( x + δ v ) ] f ^ δ ( x ) = E v ∼ U ( B ) [ f ( x + δ v ) ]
这种平滑方法具有如下性质,假设 f f G G
若 f f α α ~ f δ f ~ δ α α
^ f δ f ^ δ ( d G / δ ) ( d G / δ ) 任意 x ∈ K x ∈ K | ^ f δ ( x ) − f ( x ) | ≤ δ G | f ^ δ ( x ) − f ( x ) | ≤ δ G
证明:^ f δ ( x ) = ∫ v Pr [ v ] f ( x + δ v ) d v f ^ δ ( x ) = ∫ v Pr [ v ] f ( x + δ v ) d v v v f ( x + δ v ) f ( x + δ v ) α α α ∫ v Pr [ v ] d v = α α ∫ v Pr [ v ] d v = α S = { v : ∥ v ∥ = 1 } S = { v : ‖ v ‖ = 1 }
E v ∼ S [ f ( x + δ v ) v ] = δ d ∇ ^ f δ ( x ) E v ∼ S [ f ( x + δ v ) v ] = δ d ∇ f ^ δ ( x )
再利用 ∥ ∇ f ( x ) − ∇ f ( y ) ∥ ≤ ∥ x − y ∥ ‖ ∇ f ( x ) − ∇ f ( y ) ‖ ≤ ‖ x − y ‖
| ^ f δ ( x ) − f ( x ) | = ∣ ∣ E v ∼ U ( B ) [ f ( x + δ v ) ] − f ( x ) ∣ ∣ ≤ E v ∼ U ( B ) [ | f ( x + δ v ) − f ( x ) | ] ; Jensen ≤ E v ∼ U ( B ) [ G ∥ δ v ∥ ] ; Lipschitz ≤ G δ | f ^ δ ( x ) − f ( x ) | = | E v ∼ U ( B ) [ f ( x + δ v ) ] − f ( x ) | ≤ E v ∼ U ( B ) [ | f ( x + δ v ) − f ( x ) | ] ; Jensen ≤ E v ∼ U ( B ) [ G ‖ δ v ‖ ] ; Lipschitz ≤ G δ
从而算法为:
Algorithm. Gradient descent, reduction to non-smooth functions – ––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––– – Input f , T , x 0 ∈ K , parameter δ Let ^ f δ ( x ) = E v ∼ U ( B ) [ f ( x + δ v ) ] Apply GD on g , T , { η t = δ } , x 0 Algorithm. Gradient descent, reduction to non-smooth functions _ Input f , T , x 0 ∈ K , parameter δ Let f ^ δ ( x ) = E v ∼ U ( B ) [ f ( x + δ v ) ] Apply GD on g , T , { η t = δ } , x 0
取 δ = d G α log t t δ = d G α log t t h T = O ( G 2 d log t α t ) h T = O ( G 2 d log t α t )
暂不考虑如何计算 ^ f δ f ^ δ ^ f δ f ^ δ α δ d G α δ d G
h t = f ( x t ) − f ( x ∗ ) ≤ ^ f δ ( x t ) − ^ f δ ( x ∗ ) + 2 δ G ; for | ^ f δ ( x ) − f ( x ) | ≤ δ G ≤ h 0 e − α δ t 4 d G + 2 δ G = O ( d G 2 log t α t ) ; δ = d G α log t t h t = f ( x t ) − f ( x ∗ ) ≤ f ^ δ ( x t ) − f ^ δ ( x ∗ ) + 2 δ G ; for | f ^ δ ( x ) − f ( x ) | ≤ δ G ≤ h 0 e − α δ t 4 d G + 2 δ G = O ( d G 2 log t α t ) ; δ = d G α log t t
另外,如果在原函数 f f η t = 2 α ( t + 1 ) η t = 2 α ( t + 1 ) x 1 , ⋯ , x t x 1 , ⋯ , x t
f ( 1 t t ∑ k = 1 2 k t + 1 x k ) − f ( x ∗ ) ≤ 2 G 2 α ( t + 1 ) f ( 1 t ∑ k = 1 t 2 k t + 1 x k ) − f ( x ∗ ) ≤ 2 G 2 α ( t + 1 )
证明略
Case 3. reduction to general convex functions (non-smooth, non-strongly convex) 如果同时使用上述两个方法,会得到一个 ~ O ( d / √ t ) O ~ ( d / t ) d d O ( 1 / √ t ) O ( 1 / t )
Fenchel duality
凸优化问题,对 f f
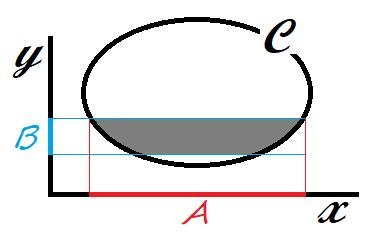

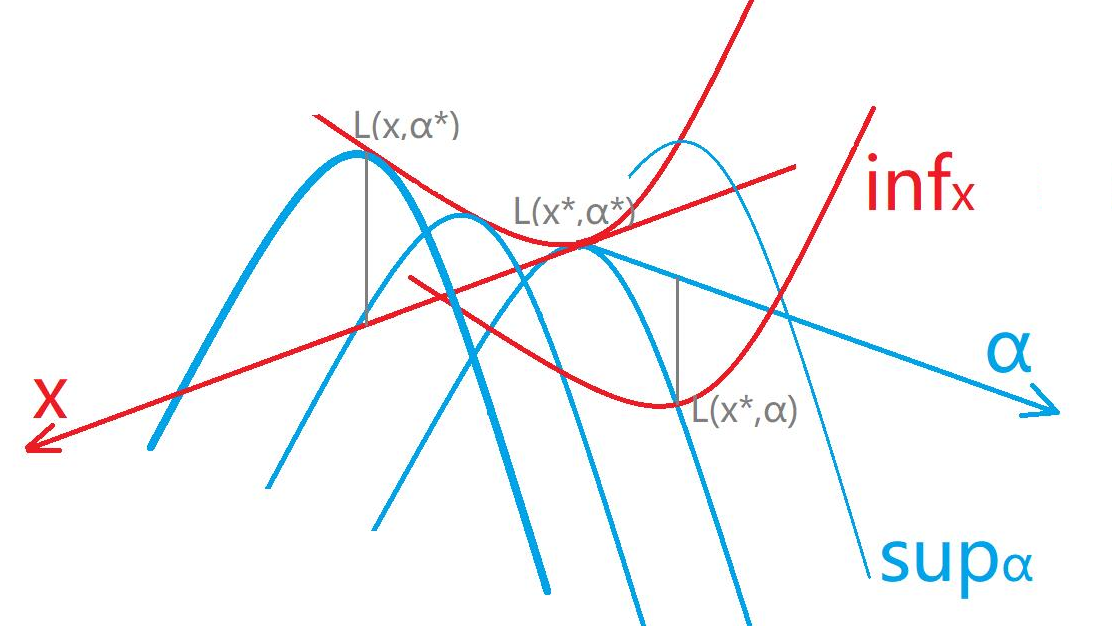 convexity, constrained optim problem, dual problem, gradient descent
convexity, constrained optim problem, dual problem, gradient descent


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· winform 绘制太阳,地球,月球 运作规律
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· 上周热点回顾(3.3-3.9)
2021-08-19 【笔记】Splay Tree