群论入门
前言
之前很喜欢群论,但是大学教材看不懂,只好作罢。
有一天在知乎上看到一个专栏,重燃了对群论的热情,决定来写一篇文章。
reference:上面那个专栏,还有维基百科。
群论是抽象代数的分支。它已经很抽象了,所以学习的时候要尽量直观理解,不然就只剩一堆符号了。本文尽量多举一些例子。
定义
给集合配上运算,就构成了代数系统。
如果代数系统没有什么性质,通常就研究出不太多东西;如果性质太多,通常用处就不广。
群就是一个非常典型、非常著名的代数系统。
群
一个集合 \(G\) 和一个二元运算 \(*:G\times G\to G\),构成一个群 \((G,*)\),当且仅当满足:
- 封闭性。对于任意 \(g,h\in G\),\(g*h\in G\)。这其实是代数系统的要求。
- 结合律。\((a*b)*c=a*(b*c)\)。
- 存在单位元 \(e\in G\),使得群中任意元素 \(g\in G\) 都满足 \(e*g=g\)。
- 对于群中任意元素 \(g\in G\),都存在逆元 \(g^{-1}\in G\) 满足 \(g^{-1}*g=e\)。
不会引起歧义的情况下,可以用 \(G\) 代替 \((G,*)\) 表示群。
举个例子,比如 \(G\) 是整数集,\(*\) 是加法。
- 任意两个整数相加,结果都是唯一的整数。
- 整数加法满足结合律。
- 整数加法的单位元是 \(0\),因为任意整数加 \(0\) 不变。
- 整数加法中,一个数的逆元是它的相反数,因为一个数加上相反数等于单位元 \(0\)。
所以整数加法构成群。
模 \(n\) 加法当然也构成群。
模质数 \(p\) 乘法也是群,因为每个数都有逆元。但是加法群里必须有 \(0\)(单位元),乘法群里不能有 \(0\)(它没有逆元)。所以模 \(n\) 加法群有 \(n\) 个元素,模质数 \(p\) 乘法群只有 \(p-1\) 个元素。
更多例子:
- 实数加法群。
- 正实数乘法群。
- \(n\) 阶可逆矩阵乘法群。
如果一个代数系统满足结合律,叫半群;如果满足结合律和存在单位元,叫幺半群。
对于一个群 \((G,*)\),如果 \(G^\prime\) 是 \(G\) 的子集,而且 \((G^\prime,*)\) 也构成群,则称群 \(G^\prime\) 是群 \(G\) 的子群,记作 \(G^\prime\le G\)。注意不是任意子集都能构成子群的,子群必须包含单位元和它里面每个元素的逆元。
如果 \(G\) 是有限集,则群 \((G,*)\) 称为有限群;反之为无限群。
注意群运算不一定满足交换律。满足交换律的群叫阿贝尔群(或者叫交换群),不满足交换律的群叫非阿贝尔群。
一般满足结合律而不一定满足交换律的运算一般被叫做“乘法”,即使它们并不是通常意义下的乘法。乘法的单位元是 \(1\),所以群的单位元又叫幺元。
阿贝尔群中的运算同时满足结合律和交换律,一般可以被叫做“加法”,单位元可以叫零元。
一个元素和它的逆元、一个元素和单位元,一定是可交换的。
对于一个群 \((G,*)\) 和它里面的一个元素 \(g\in G\),满足 \(g*g^{-1}=e\)。
证明:\(g*g^{-1}=e*g*g^{-1}={g^{-1}}^{-1}*g^{-1}*g*g^{-1}={g^{-1}}^{-1}*e*g^{-1}={g^{-1}}^{-1}*g^{-1}=e\)。
对于一个群 \((G,*)\) 和它里面的一个元素 \(g\in G\),满足 \(e*g=g\)。
证明:\(e*g=g*g^{-1}*g=g\)。
很多地方直接定义 \(\forall g\in G,ge=eg=g\) 的 \(e\) 是单位元。上面的定理说明,这个定义和我给的定义是等价的。
一些结论
单位元唯一
证明:设 \(e_1,e_2\) 是群 \(G\) 的单位元,则 \(e_1=e_1e_2=e_2\)。
逆元唯一
证明:对于群 \(G\) 中的元素 \(g\in G\),如果 \(h_1,h_2\) 是 \(g\) 的逆元,则 \(h_1=h_1e=h_1gh_2=eh_2=h_2\)。
对于 \(a,b\in G\),有且只有一个 \(c\in G\) 满足 \(ac=b\)。
证明:
存在:取 \(c=a^{-1}b\)。
唯一:如果 \(ac=b\),则 \(c=ec=a^{-1}ac=a^{-1}b\)。
于是群里可以自由地做除法。
\({a^{-1}}^{-1}=a\)
证明:\(a^{-1}\) 同时是 \({a^{-1}}^{-1}\) 和 \(a\) 的逆元,根据逆元唯一可知 \({a^{-1}}^{-1}=a\)。
消去律:若 \(ac=bc\) 则 \(a=b\)。
证明:\(ac=bc\Rightarrow acc^{-1}=bcc^{-1}\Rightarrow ae=be\Rightarrow a=b\)。
魔方群
不光数学上的东西可以用群论描述,一些现实中的东西,比如魔方和分子(《群论在化学中的应用》)也可以用群论描述。
首先确定魔方群的集合和运算。
如果你认为魔方群的运算是“拧魔方”,那就错了。这不是二元运算。
实际上,魔方群中的元素是魔方的状态。同时每个元素也代表从复原态到这个状态的变换,或者说打乱公式。
比如下面这个魔方状态就是魔方群里的一个元素。它还代表一个公式 R,也就是它的打乱公式。

(图片来源:VisualCube)
你可能会说,同一种打乱效果是可以用不同公式完成的。是的,但是这里并不区分这些公式,因为它们的效果是完全一样的。
所以严格来说,与魔方打乱结果一一对应的,不是打乱公式,而是这种打乱的变换。不管你是用哪个公式打乱的,只要效果相同,都不加区分。
其实魔方群的元素只有变换一种意思也可以,加个魔方状态只是为了直观。魔方群的运算也是关于变换而不是状态的。
魔方群的运算是变换的复合。简单地说,就是把两个公式串起来。
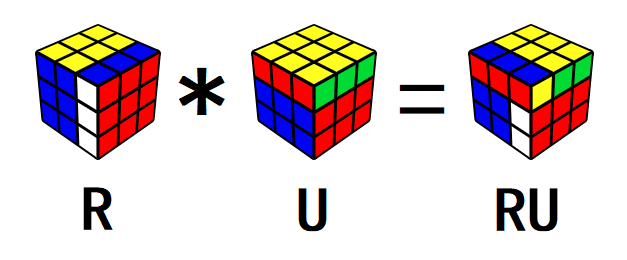
变换的复合满足结合律(不管先做 AB 再做 C,还是先做 A 再做 BC,效果是一样的);变换的单位元是恒等变换(公式为空,状态为复原状态);变换的逆元是逆变换(比如公式 RU 的逆元就是 U'R')。所以这确实构成群。
魔方群是非阿贝尔群,例如 RU 和 UR 效果不同。
但是群论告诉我们,一个公式和它的逆元一定是可交换的。比如 RUU'R'=U'R'RU。
幂和阶
幂
\(a^0:=e\)
\(a^n:=\begin{cases}aa^{n-1}&(n>0)\\a^{-1}a^{n+1}&(n<0)\end{cases}\)
群的阶就是群集合的大小。不过这里说的阶是元素的阶。
元素 \(g\in G\) 的阶是满足 \(g^m=e\) 的最小正整数 \(m\)。如果没有这样的 \(m\),称 \(g\) 有无限阶。
比如整数加法群中 \(1\) 就有无限阶。魔方群里“旋转一个面 \(90^\circ\)”的阶是 \(4\),因为转四次相当于没转。
有限群 \(G\) 中任意元素 \(g\in G\) 的阶都是有限的。
证明:列出 \(g^1,g^2,g^3,\cdots,g^{|G|+1}\)。其中有 \(|G|+1\) 个元素,但是群 \(G\) 只有 \(|G|\) 个元素。
根据抽屉原理,"数"列中一定有至少两个元素相等,设 \(g^i=g^j(i<j)\)。根据消去律,\(g^{j-i}=e\)。
元素 \(g\) 的阶一定不超过 \(j-i\)。
对称群
这里指 Symmetric group,因为还有个 Symmetry group 也可以叫对称群(一般称为空间对称群)。
给定一个数列 \(1,2,3,\cdots,n\),它有 \(n!\) 种排列。
例如,\(3\) 个数有 \(3!=6\) 种排列,如下:
与刚才魔方群思路类似,这 \(6\) 种排列都对应于置换。
比如 \(2,3,1\) 对应于 \(\begin{aligned}1\ 2\ 3\\\downarrow\ \downarrow\ \downarrow\\2\ 3\ 1\end{aligned}\)。这个置换可以写作 \(\begin{pmatrix}1,2,3\\2,3,1\end{pmatrix}\)。
当然,这个置换也可以写成 \(\begin{pmatrix}2,1,3\\3,2,1\end{pmatrix}\),交换列是不影响的。
这么写比较麻烦,所以一般写作 \((1,2,3)\),表示这个置换是 \(1\to2\to3\to1\)。我们把形如 \((a_1,a_2,a_3,\cdots,a_k)\) 的置换称为轮换。
同理,\(\begin{pmatrix}1,2,3\\3,1,2\end{pmatrix}\) 可以写成 \((1,3,2)\);\(\begin{pmatrix}1,2,3,4\\2,1,4,3\end{pmatrix}\) 可以写成 \((1,2)(3,4)\)。
\((1,2)(3,4)\) 不是轮换,但可以拆成若干个轮换;任何置换都能拆成若干个轮换。
\(\begin{pmatrix}1,2,3\\2,1,3\end{pmatrix}\),即 \((1,2)(3)\),可以简写成 \((1,2)\),但它仍然是拆成两个轮换。
同样,恒等置换可以简写成 \((1)\)。
置换的运算是置换的复合,符号是 \(\circ\)。它的意思是连续进行两次置换。
置换的复合满足结合律;单位元是恒等置换 \((1)\);逆元是逆置换(交换上下两行)。
这就是对称群,记作 \(S_n\)。例如上面介绍的三个数上的对称群记作 \(S_3\)(顺便说一句,这是最小非阿贝尔群)。
置换的复合不满足交换律,例如 \((1,3)\circ(1,2)=(1,3,2)\neq(1,2,3)\)。
有限对称群的子群称为置换群。之后有个定理说明,任何有限群都同构于一个置换群,说明了置换群的重要性。
交错群
首先需要知道,\((a_1,a_2,a_3,\cdots,a_k)=(a_1,a_2)\circ(a_1,a_3)\circ(a_1,a_4)\circ\cdots\circ(a_1,a_k)\)。归纳法易证。
称这种将两个数交换的置换为对换,并将置换全部分解成对换。
如果一个置换能分解出偶数个对换,这个置换称为偶置换;反之称为奇置换。
所有偶置换也可以构成群,因为恒等置换是偶置换,而且偶置换的逆元也是偶置换。这个群称为交错群,记作 \(A_n\)。交错群 \(A_n\) 是对称群 \(S_n\) 的子群。
交错群的例子:魔方中,不改变角块位置,则棱块位置构成 \(A_{12}\) 群。因此只有三棱换,不能只交换两个棱块。
简单证明:魔方每次旋转一个面,对棱块和角块的位置都是奇置换。所以如果角块不改变位置,是偶置换,则棱块也是偶置换。
推论:三棱换公式长度一定是偶数,PLL 中“T 字公式”长度一定是奇数。
循环群
有限循环群 \(Z_n\) 就是模 \(n\) 加法群,无限循环群就是整数加法群 \(Z\)。
正经的定义:如果群 \(G\) 中存在元素 \(a\in G\),使得群中每个元素都是 \(a\) 的幂,称 \(a\) 是群 \(G\) 的生成元,群 \(G\) 是循环群。有限循环群记作 \(Z_n\),其中 \(n\) 是群元素个数;无限循环群记作 \(Z\)。
为什么它就是模 \(n\) 加法群呢?
有限循环群中从 \(e\) 开始反复乘 \(a\),直到变成 \(e\),过程中生成的 \(a^1,a^2,a^3,\cdots,e\) 和模 \(n\) 加法群的 \(1,2,3,\cdots,0\) 是同构的。
无限循环群中用从 \(e\) 开始反复乘 \(a\),得到的 \(a^1,a^2,a^3,\cdots\) 和整数加法群的 \(1,2,3,\cdots\) 是同构的。
循环群是被研究得很透彻的一类群。如果某个群同构于循环群,那就很好。
熟悉数论的读者可能发现了,模质数 \(p\) 乘法群 \(\big(\{1,2,\cdots,p-1\},\times\big)\) 就是循环群,生成元就是 \(p\) 的原根。
显然,\(Z_n\) 中任意的 \(a^k(k\perp n)\) 都可以当做生成元,所以 \(Z_n\) 有 \(\varphi(n)\) 个生成元。于是我们轻松证明了 \(p\) 有 \(\varphi(p-1)\) 个原根。
同构
对于两个群 \((G,*)\) 和 \((H,\cdot)\),如果存在一个双射 \(f:G\to H\),满足:
对于任意的 \(g,g^\prime\in G\),都有 \(f(g*g^\prime)=f(g)\cdot f(g^\prime)\);
对于任意的 \(h,h^\prime\in H\),都有 \(f^{-1}(h\cdot h^\prime)=f^{-1}(h)*f^{-1}(h^\prime)\);
则称 \(G\) 同构于 \(H\),\(f\) 是同构映射。
同构的意思容易理解,就是完全一样。
我们来证明一下刚才提到的定理。
Cayley 定理
任何有限群 \((G,*)\) 都同构于一个置换群 \(H\)。
首先要理解,用一个元素乘整个集合,其实就是一个置换。
比如下面这个群(这个表就叫 Cayley 表):
| \(*\) | \(e\) | \(a\) | \(b\) |
|---|---|---|---|
| \(e\) | \(e\) | \(a\) | \(b\) |
| \(a\) | \(a\) | \(b\) | \(e\) |
| \(b\) | \(b\) | \(e\) | \(a\) |
用 \(a\) 去乘 \((e,a,b)\),得到 \((a,b,e)\)。这就是个置换。
任何一个元素乘 \(a\) 再乘 \(b\),相当于乘 \(a*b\)(因为 \(G\) 中的结合律)。所以整个集合进行“乘 \(a\)”的置换,再进行“乘 \(b\)”的置换,等效于进行“乘 \(a*b\)”的置换。
根据这个结论不难证明 Cayley 定理。
设群 \(G=\{g_1,g_2,g_3,\cdots,g_n\}\)。
构造置换群 \(H=\{\begin{pmatrix}g_1,g_2,g_3,\cdots,g_n\\g_kg_1,g_kg_2,g_kg_3,\cdots,g_kg_n\end{pmatrix}|1\le k\le n\}\)。
取双射 \(f(g_k)=\begin{pmatrix}g_1,g_2,g_3,\cdots,g_n\\g_kg_1,g_kg_2,g_kg_3,\cdots,g_kg_n\end{pmatrix}\)。
同态
对于两个群 \((G,*)\) 和 \((H,\cdot)\),如果存在一个映射 \(f:G\to H\),满足对于任意的 \(g,g^\prime\in G\),都有 \(f(g*g^\prime)=f(g)\cdot f(g^\prime)\),则称 \(G\) 同态于 \(H\),\(f\) 是同态映射。
如果 \(f\) 是满射,这个同态称为满同态;如果 \(f\) 是单射,这个同态称为单同态。
感觉这个定义并不是很直观,这里放一张图。
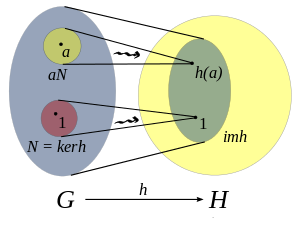
(图片来源:维基百科)
左边蓝色圈是群 \(G\),右边黄色圈是群 \(H\)。\(G\) 同态于 \(H\),同态函数是 \(h\)。
\(H\) 中灰绿色的圈是 \(H\) 的一个子群 \(\operatorname{im}(h)\),即 \(G\) 在映射 \(h\) 下的像。
由于像是 \(G\) 映射出来的,所以像中的性质在 \(G\) 中都能找到。或者说,\(G\) 包含了像的结构。
\(G\) 中红色圈里的元素都被映射到了 \(H\) 中的单位元(右边的 \(1\))。这个红色圈就是同态的核 \(\operatorname{ker}(h)\)。
这张图还很好地展示了商群的概念,之后再说,到时候对同态的理解应该会更深。
陪集
设 \(H\) 是群 \(G\) 的一个子群,\(g\in G\),则左陪集 \(gH=\{gh|h\in H\}\),右陪集 \(Hg=\{hg|h\in H\}\)。
陪集就是 \(g\) 与 \(H\) 中每个元素的乘积构成的集合,你也可以认为陪集就是 \(g\) 与 \(H\) 这个集合的乘积。
正规子群
对于群 \(G\) 的一个子群 \(H\),如果对于任意的 \(g\in G\) 与 \(h\in H\) 都有 \(ghg^{-1}\in H\),则 \(H\) 是 \(G\) 的正规子群,记作 \(H\trianglelefteq G\)。
正规子群还有一个等价的定义:如果对于任意的 \(g\in G\),有 \(gH=Hg\),那么 \(H\trianglelefteq G\)。
下面对正规子群和非正规子群各举一个例子。
观察 \(S_3\)。为了方便,我们设
列出 \(S_3\) 的表:
| \(*\) | \(\color{red}e\) | \(\color{red}a\) | \(\color{red}b\) | \(\color{blue}c\) | \(d\) | \(f\) |
|---|---|---|---|---|---|---|
| \(\color{red}e\) | \(\color{red}e\) | \(\color{red}a\) | \(\color{red}b\) | \(\color{blue}c\) | \(d\) | \(f\) |
| \(\color{red}a\) | \(\color{red}a\) | \(\color{red}b\) | \(\color{red}e\) | \(\color{blue}d\) | \(f\) | \(c\) |
| \(\color{red}b\) | \(\color{red}b\) | \(\color{red}e\) | \(\color{red}a\) | \(\color{blue}f\) | \(c\) | \(d\) |
| \(\color{blue}c\) | \(\color{blue}c\) | \(\color{blue}f\) | \(\color{blue}d\) | \(e\) | \(b\) | \(a\) |
| \(d\) | \(d\) | \(c\) | \(f\) | \(a\) | \(e\) | \(b\) |
| \(f\) | \(f\) | \(d\) | \(c\) | \(b\) | \(a\) | \(e\) |
其中子群 \(A_3=\{e,a,b\}\)(标红)是 \(S_3\) 的一个正规子群。
因为对于任意一个元素 \(g\),比如说 \(c\),无论从左边乘上 \(A_3\) 还是从右边乘上 \(A_3\),得到的结果是相同的,都是 \(\{c,d,f\}\)(标蓝)。
| \(*\) | \(\color{red}e\) | \(\color{blue}a\) | \(b\) | \(\color{red}c\) | \(d\) | \(f\) |
|---|---|---|---|---|---|---|
| \(\color{red}e\) | \(\color{red}e\) | \(\color{blue}a\) | \(b\) | \(\color{red}c\) | \(d\) | \(f\) |
| \(\color{blue}a\) | \(\color{blue}a\) | \(b\) | \(e\) | \(\color{blue}d\) | \(f\) | \(c\) |
| \(b\) | \(b\) | \(e\) | \(a\) | \(f\) | \(c\) | \(d\) |
| \(\color{red}c\) | \(\color{red}c\) | \(\color{blue}f\) | \(d\) | \(\color{red}e\) | \(b\) | \(a\) |
| \(d\) | \(d\) | \(c\) | \(f\) | \(a\) | \(e\) | \(b\) |
| \(f\) | \(f\) | \(d\) | \(c\) | \(b\) | \(a\) | \(e\) |
而 \(S_3\) 的另一个子群 \(G=\{e,c\}\),就不是正规子群。用 \(a\) 从左边乘 \(G\) 得到 \(\{a,f\}\),用右边乘 \(G\) 得到 \(\{a,d\}\)。
求证:核 \(\operatorname{ker}(h:G\to H)\trianglelefteq G\)。
先令 \(K=\operatorname{ker}(h)\),比较方便。
也就是求证:对于任意 \(g\in G\),有 \(gK=Kg\)。
考虑把 \(g\) 和 \(K\) 都映射到群 \(H\) 中。\(g\) 变成 \(h(g)\),\(K\) 变成群 \(H\) 中的单位元。任何元素和单位元的乘法都是可交换的,证毕。
商群
对于一个群 \(G\) 的正规子群 \(H\),定义它们的商群 \(G/H=\{gH|g\in G\}\)。
这个定义有点难懂。
可以这么认为,将每个元素 \(g\) 都和 \(H\) 相乘,乘积就是陪集。有些元素与 \(H\) 的乘积相同。那么将这些乘积去重后,剩下的不同乘积就构成了商群。(其实只有集合,运算还没定义呢)
如何证明商群是群呢?首先定义商群的运算。
\((gH)(g^\prime H)=\{hh^\prime|h\in gH,h^\prime\in g^\prime H\}\),也就是说,将这两个集合中的元素两两相乘,就得到乘积。
我们自然希望 \((gH)(g^\prime H)=(gg^\prime)H\),这样就可以根据 \(G\) 是群来推出 \(G/H\) 是群。
-
必要性。如果 \(x\in(gg^\prime)H\),那么 \(g\in(gH)(g^\prime H)\)。
证明:因为 \(x\in(gg^\prime)H\),所以存在 \(h\),使得 \(x=gg^\prime h=(ge)(g^\prime h)\)。
其中 \(ge\in gH\),\(g^\prime h\in g^\prime H\)。证毕。
-
充分性。如果 \(x\in(gH)(g^\prime H)\),则 \(x\in(gg^\prime)H\)。
因为 \(x\in(gH)(g^\prime H)\),所以存在 \(h,h^\prime\),使得 \(x=ghg^\prime h^\prime=gg^\prime g^{\prime-1}hg^\prime h^\prime\)。
注意到根据正规子群的性质,其中 \(g^{\prime-1}hg^{\prime}\) 是属于 \(H\) 的。
设 \(g^{\prime-1}hg^{\prime}=h^{\prime\prime}\),则 \(x=gg^\prime h^{\prime\prime}h^\prime\in(gg^\prime)H\)。
还是举那个例子,\(S_3/A_3\) 得到什么群呢?
注意到 \(e,a,b\) 乘上 \(A_3\) 后都得 \(\{e,a,b\}\),而 \(c,d,f\) 乘上 \(A_3\) 后都得 \(\{c,d,f\}\)。
所以得到的群就是这么一个小群:
| \(*\) | \(e,a,b\) | \(c,d,f\) |
|---|---|---|
| \(e,a,b\) | \(e,a,b\) | \(c,d,f\) |
| \(c,d,f\) | \(c,d,f\) | \(e,a,b\) |
也许你会问:刚才我们是那么定义陪集的乘法的,但是如果直接定义 \((gH)(g^\prime H)=(gg^\prime)H\),不就不需要 \(H\) 是正规子群了吗?
那么,我们试试用这个定义求 \(S_3/G\),其中 \(G=\{e,c\}\)。
你会发现,\(bG=dG=\{b,d\}\),但是 \((bG)(aG)=(ba)G=eG=\{e,c\}\),并不等于 \((dG)(aG)=(da)G=fG=\{a,f\}\)。所以其实这个运算的结果都是不能确定的。
这有两个显然的结论:\(G/\{e\}=G\),\(G/G=\{e\}\)。
一个群同态于它的商群(同态函数显然可以取 \(f:g\to gH\)),同态的核就是 \(H\)。
反过来说,如果群 \(G\) 同态于群 \(H\),则核 \(K\trianglelefteq G\),而且 \(G/K\cong\operatorname{im}(h)\)(像)。
再放一遍这张图。

这是一个同态,我们要证明 \(G/K\cong\operatorname{im}(h)\)。
首先证明:\(G\) 中的任意元素 \(a\),乘上核 \(K\) 得到的陪集 \(aK\),就是左边那个黄圈(黄圈的定义是,经过 \(h\) 映射后,结果和 \(a\) 一样的那些元素)。
充分性:设 \(k\in K\),则 \(h(ak)=h(a)h(k)=h(a)\),所以 \(ak\in\) 黄圈。
必要性:设 \(b\in\) 黄圈,则 \(h(ab^{-1})=h(a)h(b^{-1})=h(a)h(b)^{-1}=h(a)h(a)^{-1}=e\),所以 \(ab^{-1}\in K\)。
所以 \(\operatorname{im}(h)\) 中的元素和 \(K\) 的陪集一一对应。易证这种双射确实导致两个群同构。
Burnside 引理
久 等 了。
这两章(Burnside 引理和 Pólya 定理)在大部分群论教程里都没有,所以参考资料单独列出来:维基百科,OI-Wiki,cmd 的博客,刘汝佳的蓝书。
考虑作用在 \(n\) 个物品(如果也称为元素的话容易和群元素混)上的置换群 \(G\)(或者说 \(S_n\) 的某个子群)。
考虑用 \(G\) 中每个元素置换物品 \(k\),得到一个集合 \(E_k=\{g(k)|g\in G\}\),称为 \(k\) 的轨迹。
那对于 \(E_k\) 中的某个物品 \(l\in E_k\),有多少个置换将 \(k\) 挪到 \(l\) 呢?
恰好 \(\dfrac{|G|}{|E_k|}\) 个。
先来定义两个概念:如果在 \(g\) 置换下,物品 \(k\) 没有改变,就称 \(k\) 是 \(g\) 的不动点,\(g\) 是 \(k\) 的不动置换。
设 \(k\) 有 \(x\) 个不动置换。一定存在某个置换 \(g\) 将 \(k\) 挪到 \(l\),那么将那 \(x\) 个 \(k\) 不动置换和置换 \(g\) 复合,得到的一定是将 \(k\) 挪到 \(l\) 的置换。所以将 \(k\) 挪到 \(l\) 的置换至少有 \(x\) 个。
反过来,设将 \(k\) 挪到 \(l\) 的置换有 \(y\) 个,将这 \(y\) 个置换和 \(g^{-1}\) 复合,得到都是 \(k\) 不动置换。所以 \(k\) 不动置换也至少有 \(y\) 个。
所以将 \(k\) 挪到 \(E_k\) 中任何一个元素的置换个数相等。
这就是轨道-稳定化子定理(名字有点像化学概念?)。
接下来我们计算每个物品的不动置换个数之和。
它显然等于每个置换的不动点个数之和。
我们来把这个等量关系列出来,看看能得到什么结论。
设 \(l\) 为不同轨迹个数,\(c(g)\) 为置换 \(g\) 的不动点个数。
要计算每个物品的不动置换数之和,不妨按照轨迹计算。
对于一个轨迹 \(E\),里面的每个物品都有 \(\dfrac{|G|}{|E|}\) 个不动置换。
所以这 \(|E|\) 个物品的不动置换数为 \(|G|\)。
所以每个物品的不动置换数之和是 \(|G|l\)。
要计算每个置换不动点个数之和,就是 \(\sum\limits_{g\in G}c(g)\)。
所以得到结论 \(l=\dfrac1{|G|}\sum\limits_{g\in G}c(g)\)。
意思是说,轨迹个数等于平均不动点个数。
这就是 Burnside 引理。
Pólya 定理
和 Burnside 引理一样,\(n\) 个珠子(还是防止和物品混淆所以换个名字)上有一个置换群 \(G\)。
这次我们要给这 \(n\) 个珠子染色,一共有 \(k\) 中颜色。如果一种染色方案可以用 \(G\) 里的一种置换变成另一种染色方案,我们称两种染色方案是本质相同的。
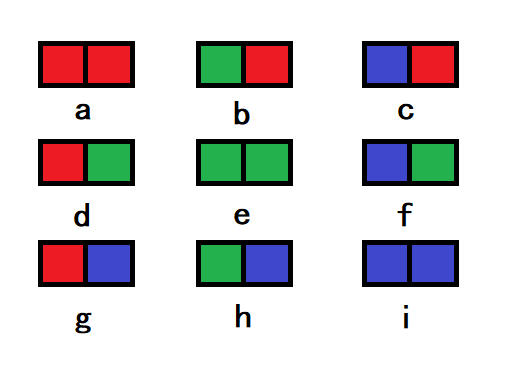
举个例子,对于下图的种染色方案 \(b\) 进行 \((1,2)\) 置换,得到染色方案 \(d\),所以 \(b\) 和 \(d\) 是本质相同的。
求本质不同的染色方案个数。
套用 Burnside 引理,但物品不是这 \(n\) 个珠子,而是 \(k^n\) 种染色方案。置换群也不再是这个 \(G\),而是作用在染色方案上的置换群 \(G^\prime\)。
还是上面那个例子,假设 \(G=\{(1),(1,2)\}\)。
\(G\) 中的置换 \((1,2)\),实际上对应于染色方案的置换 \((b,d)(c,g)(f,h)\)。
那么作用在染色方案上的置换群就是 \(G^\prime=\{(a),(b,d)(c,g)(f,h)\}\)。它的元素和 \(G\) 中的元素是对应的。
注意到本质不同的染色方案个数其实就是 \(G^\prime\) 的轨道数(想想轨道的定义)。比如上面例子中本质不同的染色方案有 \(6\) 个,刚好就是 \(6\) 个轨道 \(\{a\},\{b,d\},\{c,g\},\{e\},\{f,h\},\{i\}\)。
所以可以用 Burnside 引理求本质不同的染色方案个数,也就是 \(G^\prime\) 中每个置换的不动点个数的平均数。
\((a)\) 有 \(9\) 个不动点,\((b,d)(c,g)(f,h)\) 有 \(3\) 个不动点(即 \(a,e,i\))。
这两个数有什么好的计算方法吗?
为什么 \((b,d)(c,g)(f,h)\) 有 \(3\) 个不动点?因为两个珠子必须是同一种颜色,所以有 \(k^1\) 个不动点。为什么指数是 \(1\)?因为 \((1,2)\) 可以拆成一个轮换 \((1,2)\)。每个轮换的颜色必须相同,所以有 \(k\) 个不动点。
同理,为什么 \((a)\) 有 \(9\) 个不动点?因为两个珠子都可以随意染色,所以有 \(k^2\) 个不动点。为什么指数是 \(2\)?因为 \((1)\) 可以拆成两个轮换 \((1)(2)\),给这两个轮换染色,有 \(k^2\) 种方法。
于是总结出规律:置换 \(g\in G^\prime\) 的不动点数,等于 \(k^{\text{它对应的}\ G\ {中的置换的轮换数}}\)。
本质不同染色方案数 = \(G^\prime\) 的轨迹数 = \(G^\prime\) 的平均不动点数 = \(G\) 的平均 \(k^{\text{轮换数}}\)。
这就是 Pólya 定理。
写成公式的话就是本质不同染色方案数 \(l=\dfrac1{|G|}\sum\limits_{g\in G}k^{m(g)}\),其中 \(m(g)\) 表示 \(g\) 的轮换数。
例题:P4980 【模板】Pólya 定理
\(n\) 个珠子(点)排成圈,有 \(n\) 种颜色。\(G\) 是将圈旋转的置换群(是个循环群)。
对于 \(G\) 中的元素 \(g\),设它将第一个点转到了第 \(k\) 个位置,那么容易发现 \(m(g)=\gcd(k,n)\)。
所以这道题的答案就是 \(\dfrac1n\sum\limits_{i=0}^{n-1}n^{\gcd(i,n)}\)。剩下就是枚举 \(\gcd\),暴力算欧拉函数。



