我眼中的决策树

决策树（decision tree）

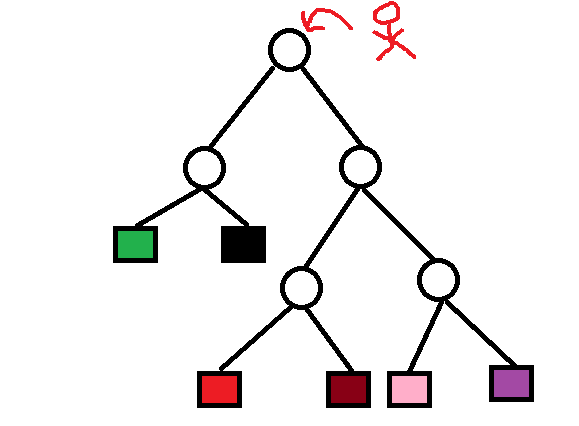
假如红色小孩要从树根回到红色格子，如果每一个圆圈表示一个岔路口，如果路口没有路标，那么小红人就会迷路，如果在每一个圆圈处都设有路标，那么小人很快就能找到红格子。而这就是决策树分类的过程。

但是问题是，如何训练出这么一棵带有路标的树呢？

决策树是属于分类，前面学习的支持向量机，K-Means，logistics回归都是分类算法，它们都涉及到概率的应用，同样决策树也使用了概率，·现实中在每一个圆圈节点处的决策并不是非零即一的，往往是该节点上的条件概率更偏向某一个方向，即某一类的概率就较大，决策树分类的时候将该节点的实例强行分到的条件概率大的那一类去。与以往一样，我们从损失函数开始。

（1）损失函数

　　决策树学习的损失韩式通常是正则化的极大似然函数。但是，如果要在所有的可能的决策树中选择出一棵最优的决策树是NP完全问题，所以现实中我们竟可能的选择一条次优决策树，也就是在每一个节点分类的时候，我们竟可能使它最优，这就类似有贪心算法。那么我们如何判定这样分类就是最优的呢？

（2）信息增益（ID3算法）

　　首先是信息熵，在化学中有熵增和熵减，例如在加热时是熵增，分子的活动性增强，制冷时相反，如果用来描述信息熵，体现了信息的随机性或者说信息的纯度。

集合1 ： {胖，矮，眼睛大，眼睛小，帅气，傻气}

集合2 ： {高，中等，矮，很高，很矮} 

集合1的中的信息很杂，有描述身高，眼睛，长相和性格类的信息，信息熵就高。

集合2全用来描述身高的信息，相对而言纯度就很高，信息熵就小。

信息熵  ：  H(X)=−∑xεXP(x)logP(x))
这种信息的不确定性往往用概率描述，在样本集合中第x类样本占比例为P（x），信息熵越高，信息的纯度就越不纯。

集合1的信息熵就可以写成Ent（D） = -（1/3log2（1/3） + 1/3log2（1/3）+ 1/6log2（1/6） + 1/6log2（1/6）） 

集合2 Ent（D） = -（1/1log2（1/1）） = 0

信息增益 ：定义为集合D的经验熵H（D）与特征A给定的条件下D的经验条件下D的经验条件熵H（D|A）的差

 

 

H（D）表示为对数据集D进行分类的不确定性。而经验条件熵H（D|A）表示在特征A给定的条件下对数据集D进行分类的不确定性，做差，表示为由于特征值A而使得对数据集D的分类的不确定性减小的程度。不同的特征值具有不同的信息增益，信息增益越大的特征具有更强的分类能力。所以只需要计算数据集（或子集）D，每一个特征的信息增益，比较它们的大小，选择信息增益最大的特征。

（3）信息增益比（C4.5）

 信息增益往往偏向于选择取值较多的特征，所以对此信息增益比可以对这一问题进行及校正。

 

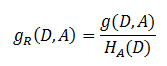
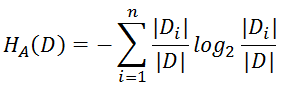
（4）基尼指数（CART算法）

 

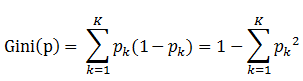
Gini（D）越小，则数据集纯度越高。

 

决策树创建代码（部分，摘自机器学习实战）：

该代码中使用信息增益算法。

#coding=utf-8

from math import log
import operator

#产生数据集（用于测试）
def createDataSet():
    dataSet = [[1,1,'yes'],
            [1,1,'yes'],
            [1,0,'no'],
            [0,1,'no'],
            [0,1,'no']]
    labels = ['no surfacing','flippers']
    return dataSet,labels
#该数据集的表格形式：
'''
            no surfacing  flippers  labels
                1            1       'yes'
                1            1       'yes'
                1            0        'no'
                0            1        'no'
                0            1        'no'

该表格中前两列是选取的两个特征（属性），每一种属性有多个取值
对于改表只有有无（0,1）两种取值
其实可以有0,1,2等多种取值
'''

#计算信息熵(经验熵)
#信息熵代表信息的纯度，纯度越高值越小
def calcShannonEnt(dataSet):
    numEntries = len(dataSet)
    labelCounts = {}
    for featVec in dataSet:
        #从右边起第一个数，也就是标签（叶子节点）
        currentLabel = featVec[-1]
        #统计不同标签的个数
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    #print (labelCounts) #输出{'yes':2,'no':3}
    shannonEnt = 0.0
    #套用公式
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        #print (prob)
        shannonEnt -= prob * log(prob,2)
    return shannonEnt


#划分数据集
#划分规则是把相同属性的集合划分在一起
#选取属性列为axis中把取值为value的样本划分在一起
def splitDataSet(dataSet,axis,value):
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet
#例如对上面的数据集划分结果：
#trees.splitDataSet(mydat,0,1)
'''
[1,'yes']
[1,'yes']
[0,'no']
'''
#注意该结果中不包含被划分的属性

#选取最好的数据集划分
def chooesBestFeatureToSplit(dataSet):
    #计算属性的个数，不包含标签列
    numFeatures = len(dataSet[0]) - 1
    #未划分时的信息熵（经验熵）
    baseEntroy = calcShannonEnt(dataSet)
    #初始化
    bestInfoGain = 0.0;bestFesture = -1
    for i in range(numFeatures):
        #提取出每一列属性值
        featList = [example[i] for example in dataSet]
        #print (featList) [1,1,1,0,0] and [1,1,0,1,1]
        #set是一个无序且不重复的元素集合
        uniqueVals = set(featList)
        #[0,1] and [0,1] 为可能选取的属性取值
        print (uniqueVals)
        newEntropy = 0.0
        for value in uniqueVals:
            #循环对每一个属性进行分类划分
            subDataSet = splitDataSet(dataSet,i,value)
            #计算划分后的信息增益减号后半部分
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)
        #计算信息增益，信息增益越大表示划分后纯度获得提升
        infoGain = baseEntroy - newEntropy
        if(infoGain > bestInfoGain):
            bestInfoGain = infoGain
            bestFesture = i
    return bestFesture

#递归创建决策树

#使用投票的算法来返回出现次数最多的分类名称
def majorityCnt(classList):
    classCount={}
    for vote in classList:
        if vote in classCount.keys():
            classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classCount.iteritems(),key=operator.itemgetter(1),reverse=True)
    return sortedClassCount[0][0]

#创建树的代码
def createTree(dataSet,labels):
    #classList返回的是标签['yes','yes','no','no','no']
    classList = [example[-1] for example in dataSet]
    #计数同classList[0]相同的个数是否等于总长度
    #也就是判断这些数据标签是否相同
    #是的话就返回（叶子节点）
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    #遍历完所有的特征时返回出现最多的类标签
    if len(dataSet[0]) == 1:
        #print (majorityCnt(classList))
        return majorityCnt(classList)
    #选择最好的属性划分
    bestFeat = chooesBestFeatureToSplit(dataSet)
    #取出字典中对应的标签
    bestFeatLabel = labels[bestFeat]
    #初始化树，树的根节点是一开始选出的最好的标签
    myTree = {bestFeatLabel:{}}
    #删除此标签
    del(labels[bestFeat])
    #把最优特征下的所有属性取值全部选出来（例如西瓜纹理下的，青绿，乌黑，浅白等）
    featValues = [example[bestFeat] for example in dataSet]
    #去重
    uniqueVals = set(featValues)
    #遍历特征，创建决策树
    for value in uniqueVals:
        subLabels = labels[:]
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet,bestFeat,value),subLabels)
    return myTree

 

以机器学习实战——使用决策树预测隐形眼镜类型为例

决策树建树过程分解：

 

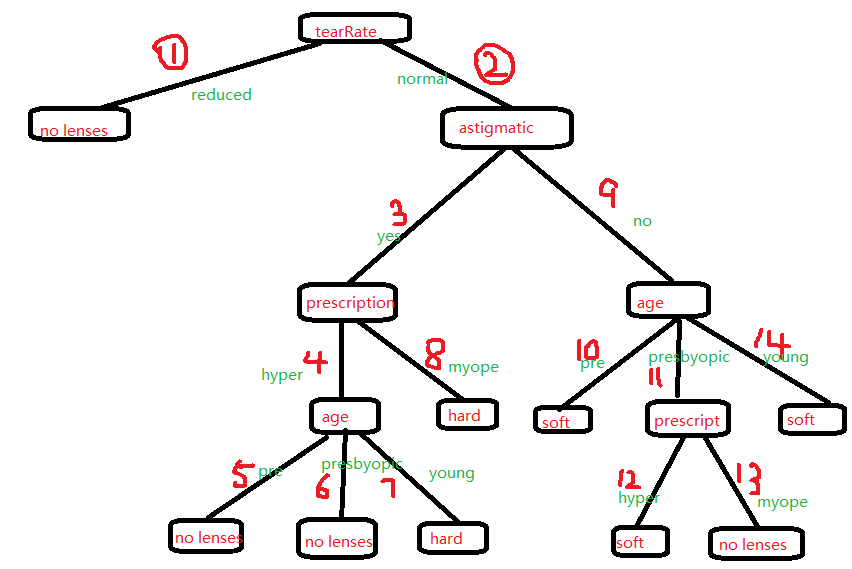
序号是这个树生成的过程顺序，可以对照代码捋一遍，便清楚树的建造过程。