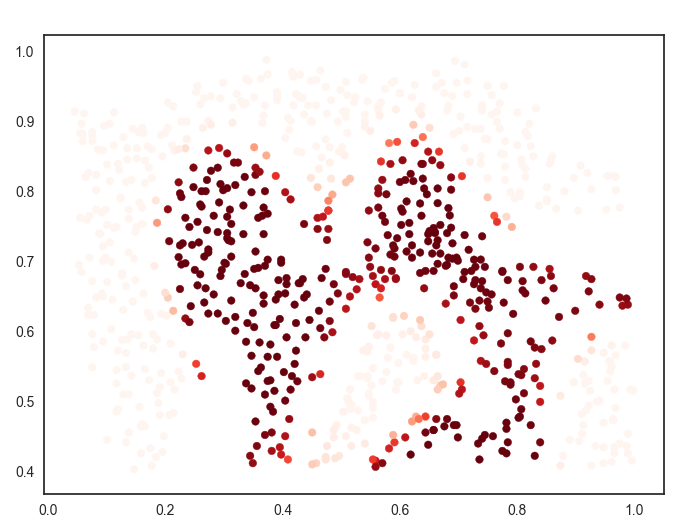
支持向量机（SVM）举例

例（1） 无核（No kernel or linear kernel）

　　代码和数据集来自于https://github.com/fengdu78/Coursera-ML-AndrewNg-Notes

#coding = utf-8
import numpy as np
import pandas as pd
import sklearn.svm
import seaborn as sns
import scipy.io as sio
import matplotlib.pyplot as plt

#数据的加载
mat = sio.loadmat('./data/ex6data1.mat')
print(mat.keys())
data = pd.DataFrame(mat.get('X'),columns=['X1','X2'])
data['y'] = mat.get('y')
#print (data)
print (data.head())

#样本展示
#画布的大小
fig , ax = plt.subplots(figsize=(8,6))
#scatter（输入量x1，输入量x2，点的大小，点的颜色，画布颜色）
ax.scatter(data['X1'],data['X2'],s=50,c=data['y'],cmap='Reds')
ax.set_title('Raw data')
ax.set_xlabel('X1')
ax.set_ylabel('X2')
#plt.show()

#try C = 1
svc1 = sklearn.svm.LinearSVC(C=1,loss='hinge')
#根据所给的训练集调整模型
svc1.fit(data[['X1','X2']],data['y'])
#返回平均精确值对于所给的测试数据和label
score = svc1.score(data[['X1','X2']],data['y'])
print (score)

#对于给定的样本预测置信度
data['SVM1 Confidence'] = svc1.decision_function(data[['X1','X2']])
fig , ax = plt.subplots(figsize=(8,6))
ax.scatter(data['X1'],data['X2'],s=50,c=data['SVM1 Confidence'],cmap='RdBu')
ax.set_title('SVM(C=1) Decision Confidence')
#plt.show()

#try C = 100
svc100 = sklearn.svm.LinearSVC(C=100,loss='hinge')
#根据所给的训练集调整模型
svc100.fit(data[['X1','X2']],data['y'])
#返回平均精确值对于所给的测试数据和label
score = svc100.score(data[['X1','X2']],data['y'])
print (score)

#对于给定的样本预测置信度
data['SVM100 Confidence'] = svc100.decision_function(data[['X1','X2']])
fig , ax = plt.subplots(figsize=(8,6))
#置信度越高，则点的颜色越深
ax.scatter(data['X1'],data['X2'],s=50,c=data['SVM100 Confidence'],cmap='RdBu')
ax.set_title('SVM(C=100) Decision Confidence')
plt.show()

print (data.head())

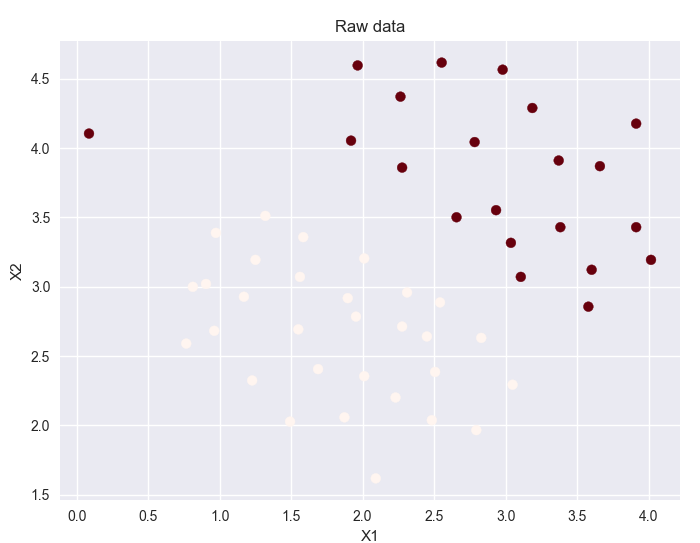
样本展示：

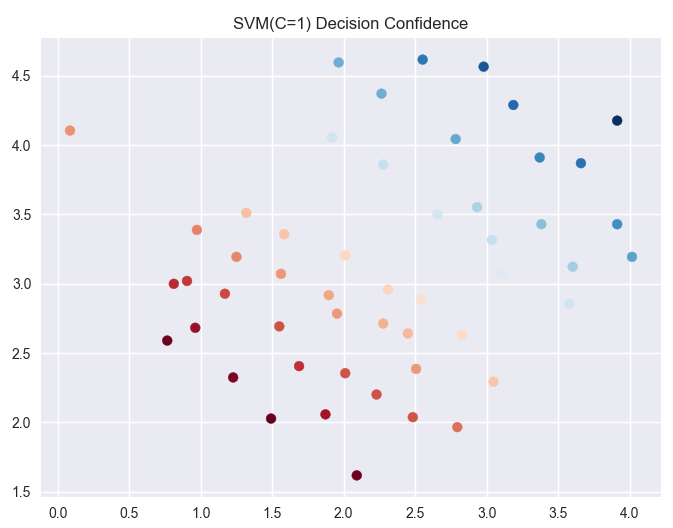
参数C=1时：

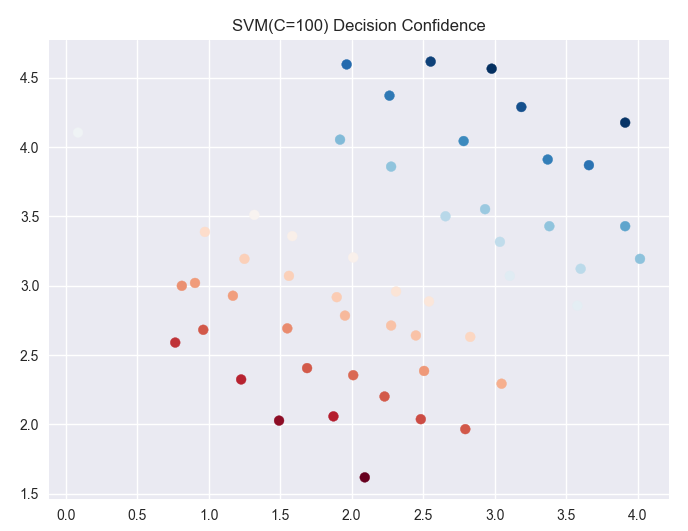
参数C=100时：

输出值：

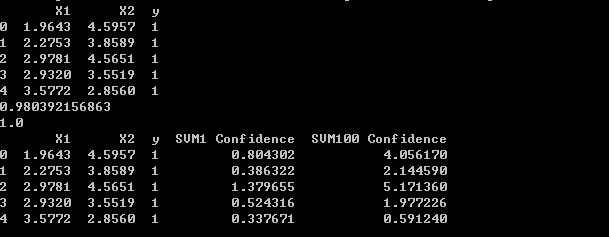
上半部分是数据集前五行，X1，X2表示坐标，y为标签。下半部分，加上了在C=1时和C=100时的置信度

通过两个图像对比：

C值越大对于训练集的表现越好，但是间隔减小也就是对于噪声等干扰的容忍度减小，可能引发过度拟合（overfitting），这时说明对于噪声的惩罚力度太大。C趋近于零的时候，就只会考虑间距越大越好，如果好的话会忽略一些异常点，但是有的时候会造成欠拟合。所以C=1的图像和C=100的图像对比，我们发现，C=100时分割线附近的点的颜色明显要比C=1分割线附近的点的颜色浅，说明C=100的间隔要小于C=1的分割间距。

 

 （2） 高斯核函数（Gaussian SVM）

 　　

#coding=utf-8
import matplotlib.pyplot as plt
from sklearn import svm
import numpy as np
import pandas as pd
import seaborn as sns 
import scipy.io as sio

#kernel function 高斯函数
def gaussian_kernel(x1,x2,sigma):
    return np.exp(- np.power(x1 - x2,2).sum() / (2*(sigma ** 2)))

x1 = np.array([1,2,1])
x2 = np.array([0,4,-1])
sigma = 2

result = gaussian_kernel(x1,x2,sigma)
print (result)

mat = sio.loadmat('./data/ex6data2.mat')
print (mat.keys())
data = pd.DataFrame(mat.get('X'),columns=['X1','X2'])
data['y'] = mat.get('y')

print (data.head())

print (data.shape)

#展示原始数据
#set( )通过设置参数可以用来设置背景，调色板等
sns.set(context="notebook",style="white",palette=sns.diverging_palette(240,10,n=2))
sns.lmplot('X1','X2',hue='y',data=data,
            size=5,
            fit_reg = False,
            scatter_kws={"s":10}
            )
#plt.show()

#使用高斯核函数
svc = svm.SVC(C=100,kernel='rbf',gamma=10,probability=True)
'''
 C：C-SVC的惩罚参数C?默认值是1.0

C越大，相当于惩罚松弛变量，希望松弛变量接近0，即对误分类的惩罚增大，趋向于对训练集全分对的情况，这样对训练集测试时准确率很高，但泛化能力弱。C值小，对误分类的惩罚减小，允许容错，将他们当成噪声点，泛化能力较强。

l  kernel ：核函数，默认是rbf，可以是‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’ 
    用于预处理数据矩阵成为核矩阵

  　　0 – 线性：u'v

 　　 1 – 多项式：(gamma*u'*v + coef0)^degree

  　　2 – RBF函数：exp(-gamma|u-v|^2)

  　　3 –sigmoid：tanh(gamma*u'*v + coef0)

l  gamma ： ‘rbf’,‘poly’ 和‘sigmoid’的核函数参数。默认是’auto’，则会选择1/n_features
l  probability ：是否采用概率估计？.默认为False
'''
print (svc)

#训练模型
svc.fit(data[['X1','X2']],data['y'])
#给出平均精确值
svc.score(data[['X1','X2']],data['y'])

#计算样本X中可能输出的概率，返回的是（n_sample，n_class）,本实例是正负类，所n_class=2
#返回是m*2的数组，正样本概率和负样本概率
predict_prob = svc.predict_proba(data[['X1','X2']])[:,1]
#print (predict_prob)
fig , ax = plt.subplots(figsize=(8,6))
#通过概率值来分割样本
ax.scatter(data['X1'],data['X2'],s=30,c=predict_prob,cmap='Reds')
plt.show()

 

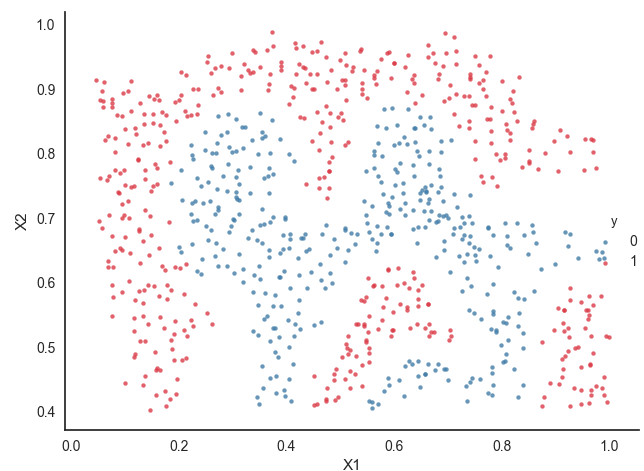
样本展示：

代码中主要过程是：

（1）训练模型

（2）计算样本X中可能输出的概率，返回的是（n_sample，n_class）,本实例是正负类，所n_class=2

 　　所以返回矩阵中，有正样本概率和负样本概率。

 

predict_prob = svc.predict_proba(data[['X1','X2']])[:,0]

   这句代码是取预测的负样本概率存放在predict_prob中。

predict_prob = svc.predict_proba(data[['X1','X2']])[:,1]
这句代码是取预测的正样本概率存放在predict_prob中。

分别查看结果：

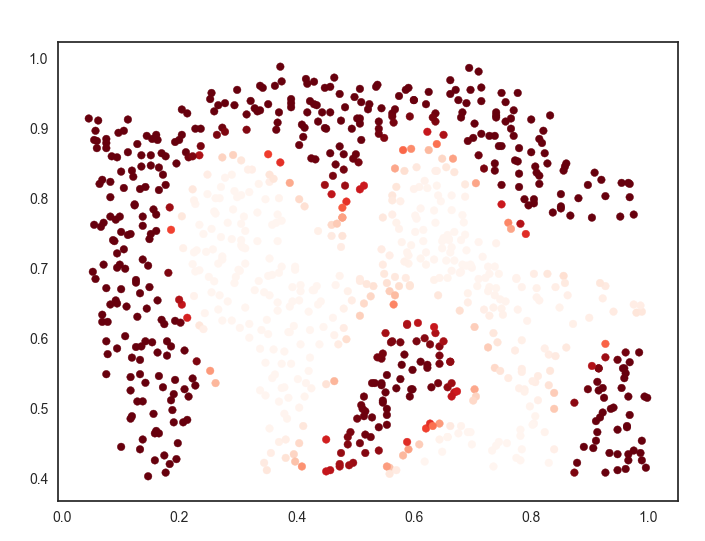
对于这两张图，我们应该关注正负样本分界线出的样本点，很明显它不像其它点，根据点的颜色的深浅判断，概率几乎变化不大，只有在分割线处，概率发生变化，这能说明什么呢？

如果根据https://www.cnblogs.com/zhxuxu/p/9590685.html 这篇博客中所说的，如果把样本点映射成地标，再通过高斯核函数计算出相对应的特征向量（一个特征向量对应一个样本），在分割线处距离明显要大于其他位置，距离影响样本点的概率，这样就可以理解了。

通过本例，我对支持向量机又有的深刻的理解。

如有不对，还望指教！！！