我眼中的支持向量机（SVM）
看吴恩达支持向量机的学习视频，看了好几遍，才有一点的理解，梳理一下相关知识。
（1）优化目标：
支持向量机也是属于监督学习算法，先从优化目标开始。
优化目标是从Logistics regression一步步推导过程，推导过程略
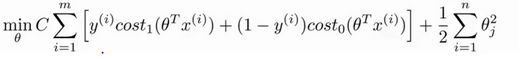
这里cost1和cost0函数图像为：
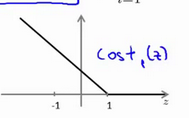
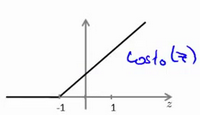
Z是theta的转置和x的内积。当Z>=1时，cost1 = 0. 当Z<=-1时,cost0 = 0.
因为要最小化损失函数
if y = 0 :我们希望Z >=1 (不仅仅要大于零，这里是与逻辑回归相比，如下图)
if y = 0 :我们希望Z <=-1 (不仅仅要小于零，这里是与逻辑回归相比，如下图)
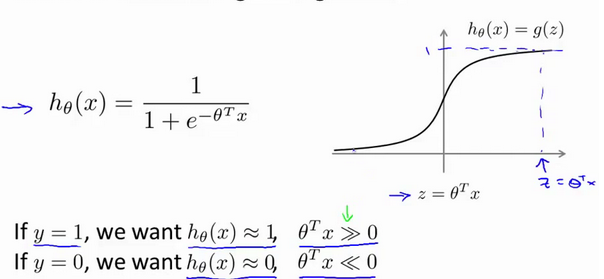
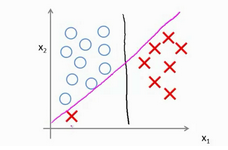
通过这样的对比发现支持向量机的要求要比逻辑回归更加严格，这也说明了支持向量机的安全距离更高。就像下图中黑线，如果你想知道为什么，下一部分将会揭晓。
有的时候样本并没有上图分的那样好，可能有几个点不符合，支持向量机将会对此很敏感，例如下图，这样的分割（红线）并不是我们想要的，这就需要调整参数C的值，当C的值不是很大的时候将会忽略一些异常点，让分割更加合理。
接下来从数学层面上分析，为什么会得到上图的分割
将会对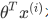
进一步转化，学习向量内积的相关知识，可以转化为
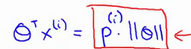，如下图，表示距离
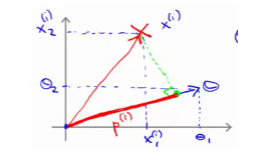
那么我们替换一下上面的表达式为下图
好，接下来，用一个例子说明，假如要对下图划分，假如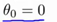
，简化问题，使：
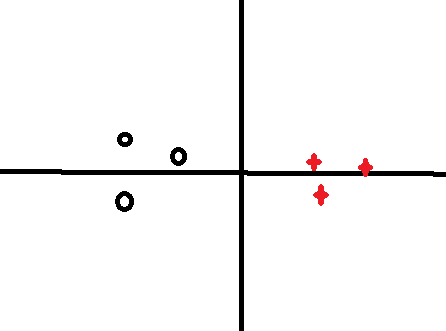
如果把它分割成这样，绿色线是决策边界和theta向量成90度夹角：
如果这样分的话，可以看到P1和P2的值相对较小，而要满足
这样就会导致theta增大，所以还要进行优化调整。
如果这样分呢，显然距离P1，P2增大了，相应的theta的值也要减小，有人问，为什么要theta减小，别忘了我们最初的目的是让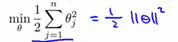
最小，这样做是不是更加合理了呢，所以说支持向量机是一个大间距分类器。
当然，以上都是简单的线性分类，如果变得更复杂点该怎样解决呢？例如
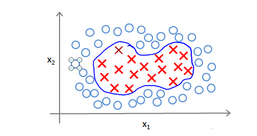
对于这样的样本，你可能会使用多项式来设置假设函数，但是如果特征再多点，像一张图片，那么将会十分麻烦，所以就有了核函数。
根据我的理解，假如你想在地图上确定你现在属于哪一个区域，你需要找到几个地标性建筑，然后把自己的位置和地标建筑进行比较，就能确定了。就是这个道理。
给定一个训练样本x，我们利用x的各个特征与我们预先选定的地标(landmarks)L1，L2，L3的近似程度来选取新的特征f1，f2，f3。
变换用的核函数有很多，这里使用高斯核函数，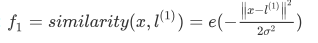
，也就是x距离L1近了为1，远了为0，其它也是一样道理。
假如我们已经知道theta1，theta2，theta3的值，那么给一个测试样本x，根据高斯核函数计算出三个特征值。大于零预测y值为1，小于零为0，如下图所示。
如何得到地标，可以把训练集中的样本点当成地标，这样
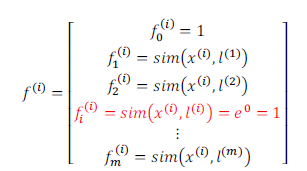
m表示训练集元素的个数。这样损失函数为：
当然还可以选择其他核函数。
