我眼里K-Means算法

在我眼里一切都是那么简单，复杂的我也看不懂，最讨厌那些复杂的人际关系，唉，像孩子一样交流不好吗。

学习K-Means算法时，会让我想起三国志这个游戏，界面是一张中国地图，诸侯分立，各自为据。但是游戏开始，玩家会是一个人一座城池（我比较喜欢这样，就有挑战性），然后不断的征战各方，占领城池

不断的扩大地盘，正常来说，征战的城池是距离自己较为近的，然后选择这些城池的中心位置作为主城。所以过来一段时间后，地图上就会出现几个主要的势力范围，三足鼎立正是如此。这个过程和K-Means算法十分相似。

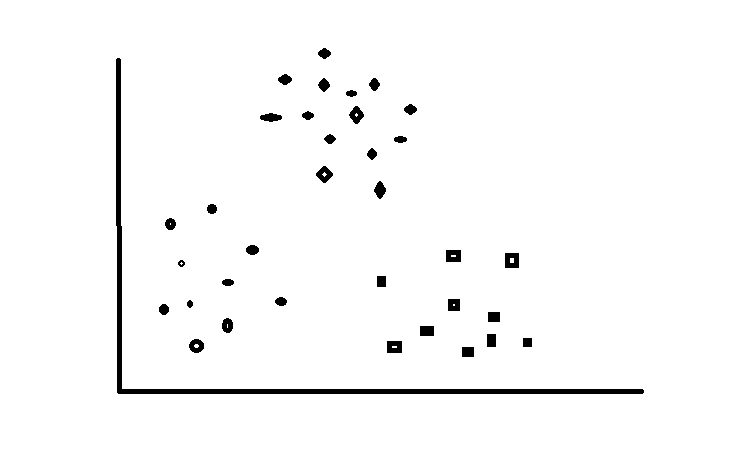
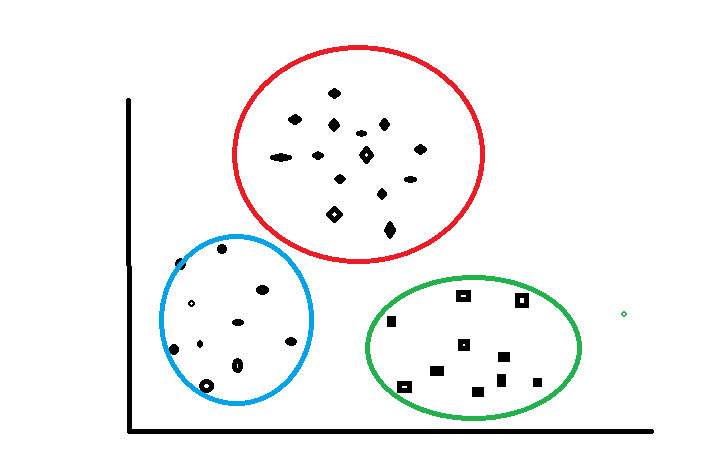
接下来我们以下图为游戏地图为例来讲解K-Means算法，地图中的每一个城池为一个数据样例（包含城池的坐标），假如游戏开始设定三个游戏玩家（三个聚类中心K），游戏目的希望最后三个玩家各自为据形成右图的格局。开始游戏！

                                                                         

 

 

K-Means（k均值算法）：

一开始先要介绍算法的整体流程

（1）随机初始化聚类中心的位置

（2）计算每一个点到聚类中心的距离，选取最小值分配给k(i)

　　

 

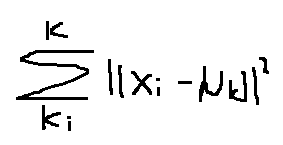
（3）移动聚类中心（其实就是对所属它的样本点求平均值，就是它移动是位置）

　　

 

（4）重复（2），（3）直到损失函数（也就是所有样本点到其所归属的样本中心的距离的和最小）

最后整体分类格局会变得稳定。

优化目标，也就是之前我们经常提到的损失函数

 　　

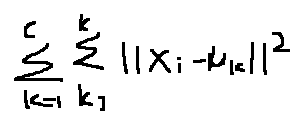
在不断的循环过程中，聚类中心也在不断地更新，直到上式距离总和收敛精确值的时候，获得最优解。

 

（1） 随机初始化

　　为了游戏的公平性，使用随机的方式把三个游戏玩家分配到地图上三个城池中（这里需要注意聚类中心的个数一定要小于数据样本的个数）。随机初始化会遇见下面几种情况

　　1 好的情况

　　

　　这种情况最为好，因为三个聚类中心已经很好的散布在三个主要的样本类上，再执行下面的算法就可以形成我们想要的分类。

   2

　　

　　这种情况就不太好，红点和绿点一开始就分配在以起，所以一开就会产生对立，对于不好的初始化可能会产生以下聚类结果

　　

 

　　这种情况就是就很糟糕了，不符合要求。

　　对于这种情况我们没有很好的解决办法，可以尝试多次初始化，获取最好的结果，例如设置1000次随机初始化，选取损失函数值最小的一个。

 还有一种情况，对于有些数据集天生分布不明显的数据集，怎么才能正确的选择聚类中心的个数，例如：

 

使用（elbow method）“胳膊肘算法”：

 获取损失函数和聚类中心K的函数图像，大致有两种图像类型

 

 

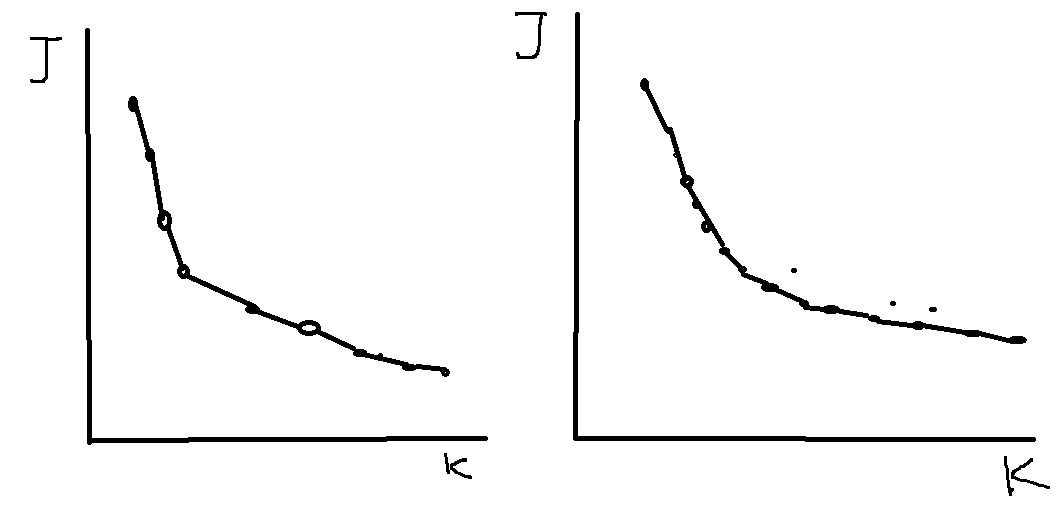
左图的拐点明显，而右图的拐点不是很明显，对于左图我们可以选取拐点处的k作为聚类中心的个数，而如果是右图，那么就需要根据情况选取，比如说，如果数据集是衣服的尺码的数据，如果你想确定这些衣服的尺码类型，那么根据你想要分成几种尺码类型决定（例如：L，M，S）（还有，M,L，XL，XXL，S）