logistics回归简单应用(二)
警告:本文为小白入门学习笔记
网上下载的数据集链接: https://pan.baidu.com/s/1NwSXJOCzgihPFZfw3NfnfA 密码: jmwz
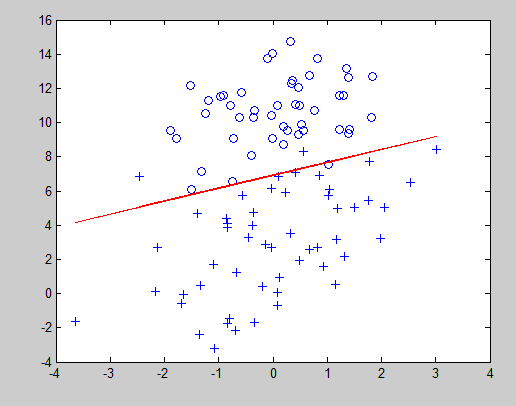
不知道这个数据集干什么用的,根据直观分析应该属于分类问题,有两个变量X1和X2,Y取值非零即一,用MATLAB分析发现第二列对Y的影响较为明显
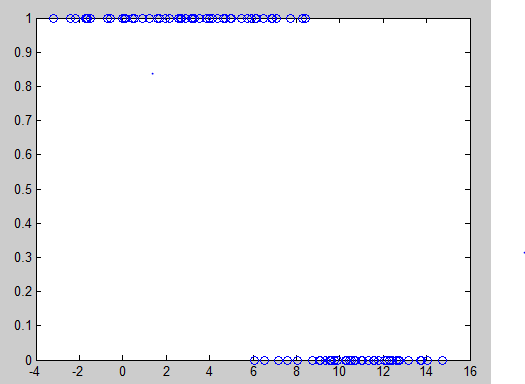
大致以8为分界线,8右边Y值为0,8左边Y为1.
首先假设舍去属性X1,设数据集为(X2,Y)。然后分别用线性回归(Liner regression)和逻辑回归(logistics regression)对数据集进行分类分析比较。最后再把属性X1加上看看结果怎么样。
(1)假设函数(hypothesis function):
参数(parameter)设为w = [w1;w2];
hw(x) = w1 + w2x;
(2)代价函数(cost function):
J(w) = 1/2m∑(hw(x(i)) - y(i))^2 ; (m是数据集的个数,乘上2是为了后来求导时候方便)
J(w) = 1/200∑(w1 + w2x(i) - y(i))^2;
(3)梯度下降算法(gradient descent algorithm)求解出参数w1和w2:
w1 := ðJ(w1,w2)/ðw1 = 1/m∑(hw(x(i)) - y(i));
w2 := ðJ(w1,w2)/ðw2 = 1/m∑(hw(x(i)) - y(i))x(i);
(ð表示求偏导)
repeat until convergence {
w1 := w1 - α1/m∑(hw(x(i)) - y(i));
w2 := w2 - α1/m∑(hw(x(i)) - y(i))x(i);
};
(α是步长,使用MATLAB/octave是自动选取)
注意:在每次更新w1,w2时候应该注意更新的顺序,应该是先一起计算再一同更新,也就是每一次更新时,w1和w2的值都在变化。
接下来就使用MATLAB(octave也可以)来测试整个分析过程是否正确,然后再用python代码实现。
(4)MATLAB模拟(octave同理可用)
新建一个costFunction.m文件 写入函数:
function[jval,gradient] = costFunction(w)
filename = 'testSet.txt';
A = importdata(filename);
x = A(:,2);
y = A(:,3);
m = 0;
for i = 1:100
m = m + (w(1) + w(2) * x(i) - y(i)).^2;
end
jval = 1/200 * m;
n = 0;
for i = 1:100
n = n + (w(1) + w(2) * x(i) - y(i));
end
gradient(1) = 1/100 * n;
n = 0;
for i = 1:100
n = n + (w(1) + w(2) * x(i) - y(i))*x(i);
end
gradient(2) = 1/100 * n;
命令行窗口输入:
>> options = optimset('GradObj','on','MaxIter',100);
>> initialW = zeros(2,1);
>> [optW,functionVal,exitFlag] = fminunc(@costFunction,initialW,options)
返回结果:
optW =
1.1202
-0.0897
functionVal =
0.0385
exitFlag =
1
结果表明:
w1 = 1.1202 ; w2 = -0.0897 ; 函数返回的结果是0.0385(这个值越接近零,表示拟合的越好) ;extiFlag = 1表示收敛
(5)画出图像
既然已经得到了w1和w2的值那就可以画出假设函数(hypothesis function)看看这么样吧!!
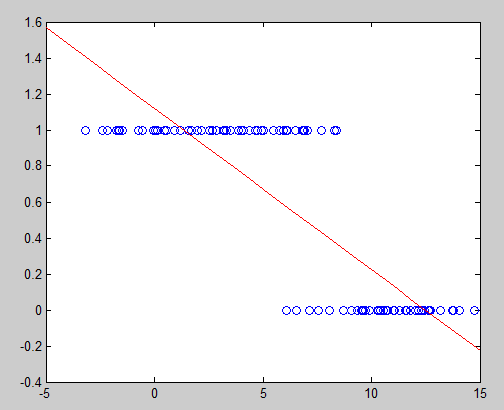
结果是这样的,这是线性回归结果,但是对于分类为题,这样做并不是什么好主意(只是用它来作比较练练手),所以接下来选用logistics回归试一试。
因为对于这个数据集,函数值Y = 0 or 1,所以希望对于输入值x,假设函数 0<=Y<=1,这样最好不过了!
不同之处需要改变假设函数(hypothesis function):
hw(x) = g(w'x) (这里'为转置的意思)
g(z) = 1/(1+e‾z)
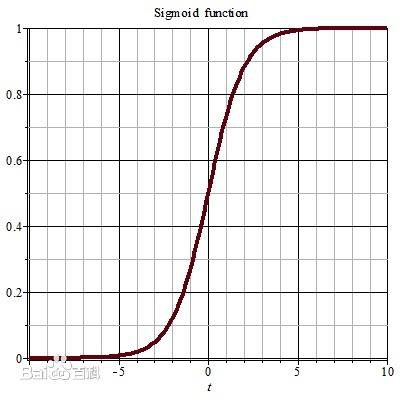
那么这个时候hw(x)表示的什么意识呢?函数的输出值是对输入值x可能性的评价
例如:判断一个肿瘤(tumor)是良性还是恶性, 假如现在只取肿瘤大小x这个属性进行分析。
如果当x为一定值时 hw(x) = 0.7,可以说这个肿瘤有70%的概率是恶性肿瘤。
所以:hw(x) = P(y=1|x;w) (表示在x,w的条件下,y=1的概率是多少)
(1)首先让表达式以矩阵的形式表示
w = [w1;w2] ; x = [1;x];
z = w1 + w2x = w'x;
hw(z) = 1/(1+e‾z);
然后如何计算w1和w2呢?
(2)代价函数(cost function)
J(w) = 1/m∑1/2(hw(x(i)) - y(i))^2 ;
设:cost(hw(x),y) = 1/2(hw(x) - y)^2;
cost(hw(x),y)= -log(hw(x)) if y=1;
cost(hw(x),y)= -log(1 - hw(x)) if y=0;
合并成一个连续函数:
cost(hw(x),y)= -y*log(hw(x)) - (1-y)*log(1-hw(x));
代入代价函数中得:
J(w) = -1/m[∑-y(i)*log(hw(x(i))) - (1-y(i)*log(1-hw(x(i)))];
(3)梯度下降算法(gradient descent algorithm)
repeat{
wj :=wj - α(δJ(w)/δwj), (j = 1,2......n)
}
(α学习步长)
求偏导(懒得打字了):
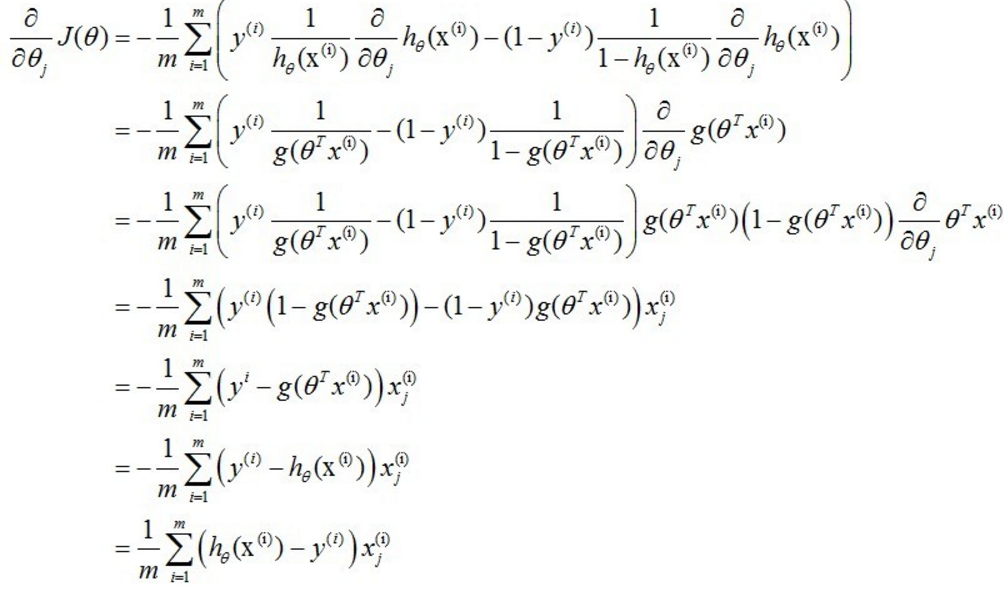
更新过程就可以写成
repeat{
wj := wj - α1/m∑(hw(x(i)) - y(i))xj(i) ; (j = 1,2......n)
}
其中x0 = 1; 是不是十分眼熟,这个式子和上面的式子一样,只是假设函数hw(x)不同罢了。
(4)MATLAB实现
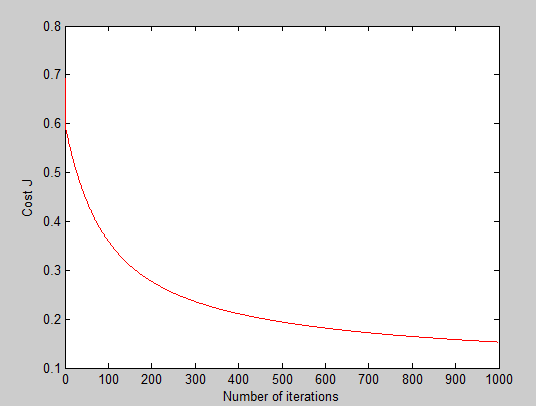
决策曲线: